Splay 树
Splay 树的思想为通过双旋来改善数的平衡。它的基本操作是将一个点旋转至根或另一结点的儿子。在旋转过程中,Treap 树只是一层一层地旋转,不能改善平衡性;而 Splay 树一次考虑两层,再通过不同的方式来改善平衡。
1. Splay 旋转
有两种方式,分别为一字旋和之字旋。记单旋时左旋为 zay,右旋为 zig。
若要旋转点 \(u\) 至根或另一结点 \(p\) 的儿子,那么分为以下几种情况:
若 \(u\) 的父亲是根或 \(p\):
此时只需要一次单旋即可,\(u\) 会上升一层。
否则 \(u\) 有父亲 \(f\) 和祖父 \(g\)。若 \(u,f,g\) 在同一直线上,那么先旋转 \(f\),再旋转 \(u\)。否则旋转两次 \(u\)。
我们来看一下它的旋转过程:
- 单旋
做一次 zig 或 zag 即可。
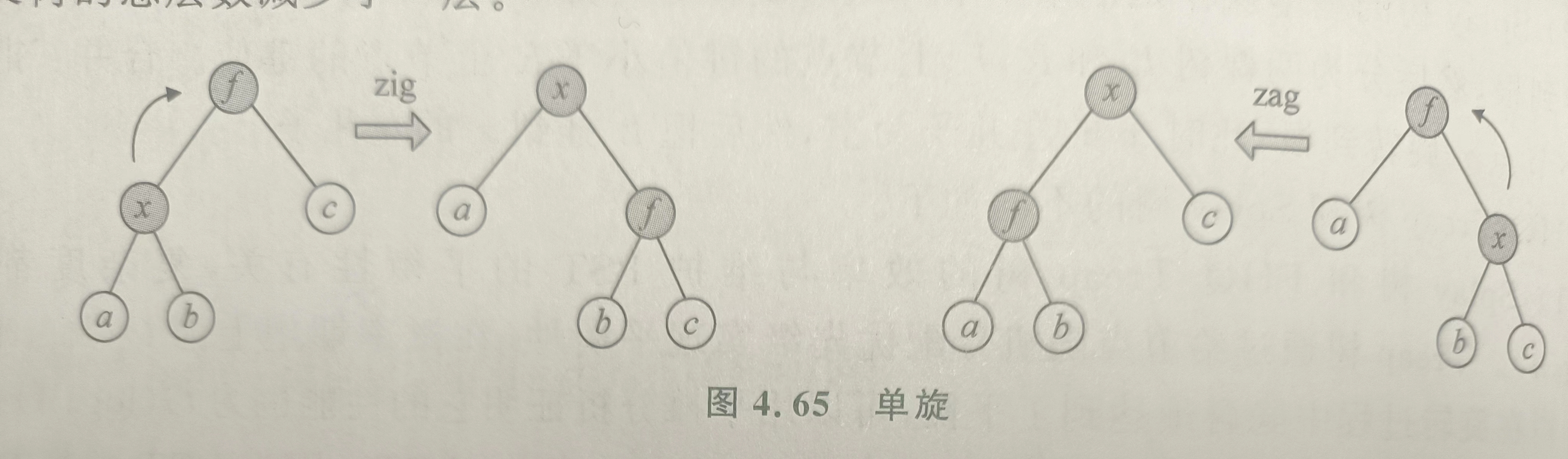
- 一字旋
做 zig-zig 或 zag-zag。应先旋转 \(f\),再旋转 \(u\)。下图是 zig-zig 的过程。
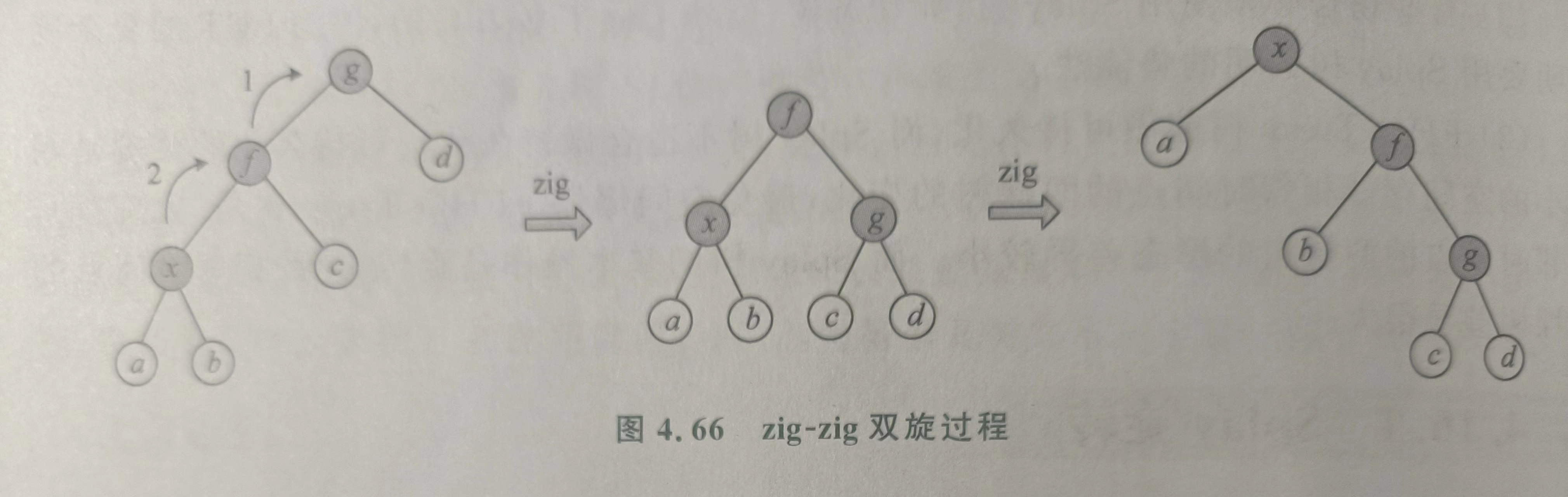
在极端情况下,比如树是一条链,那么一字旋可以改善平衡。如下图。
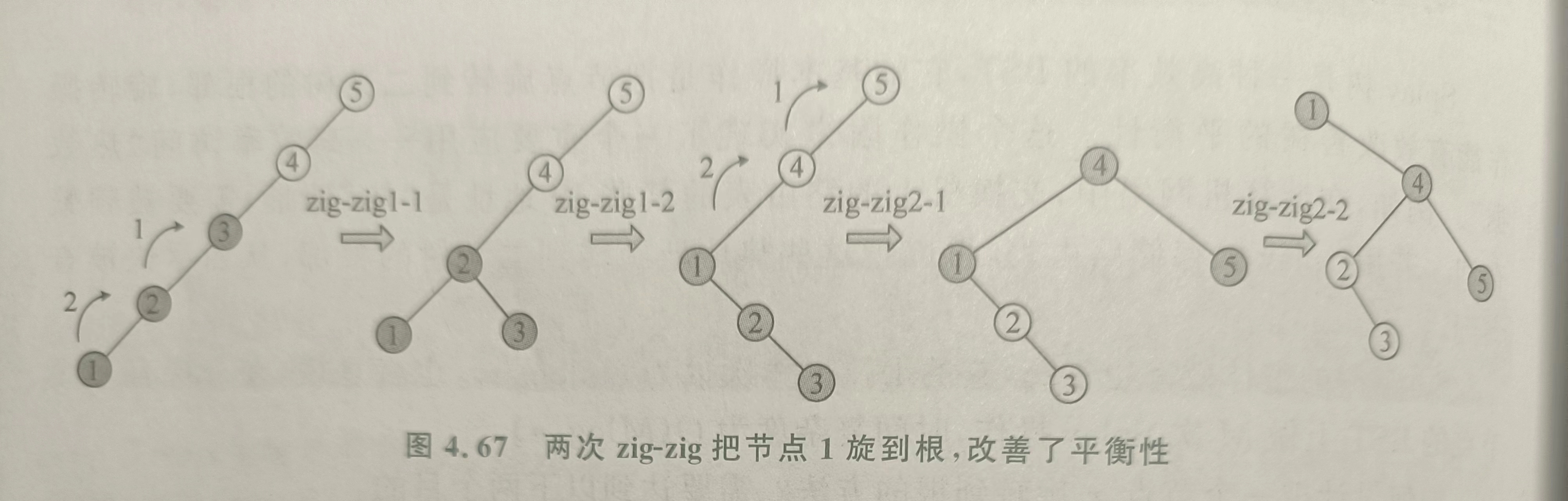
如果只是一层一层地单旋,那么不能改善平衡性。
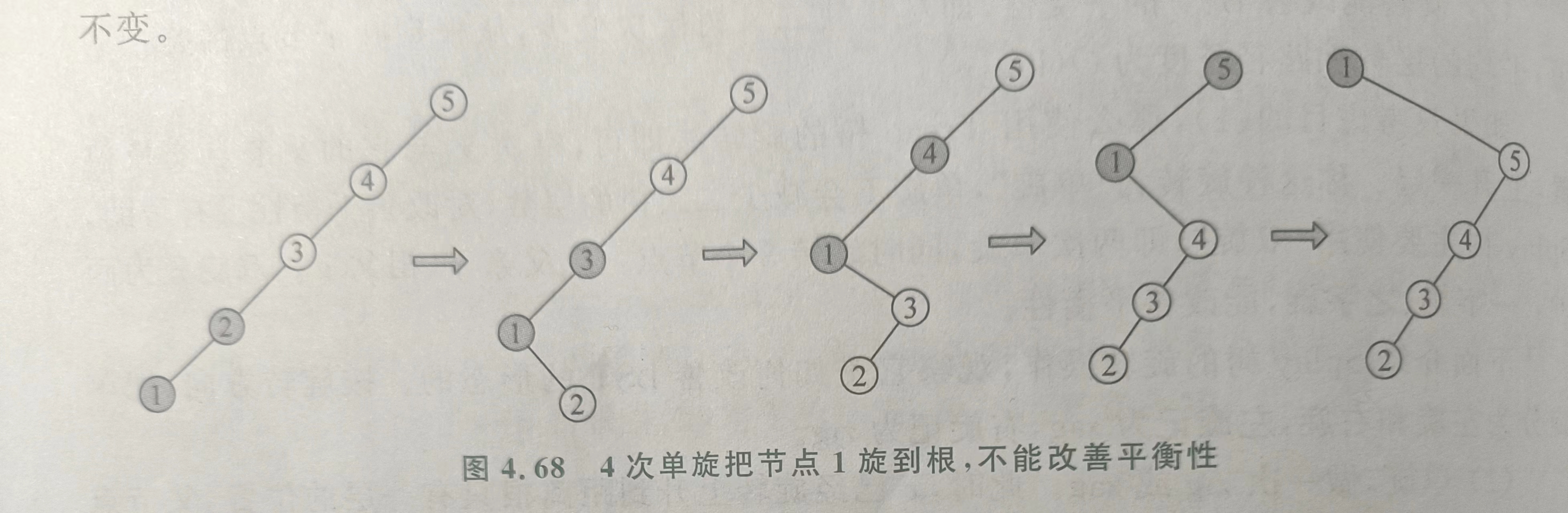
- 之字旋
做 zig-zag 或 zag-zig。先旋转 \(u\),在旋转 \(f\)。
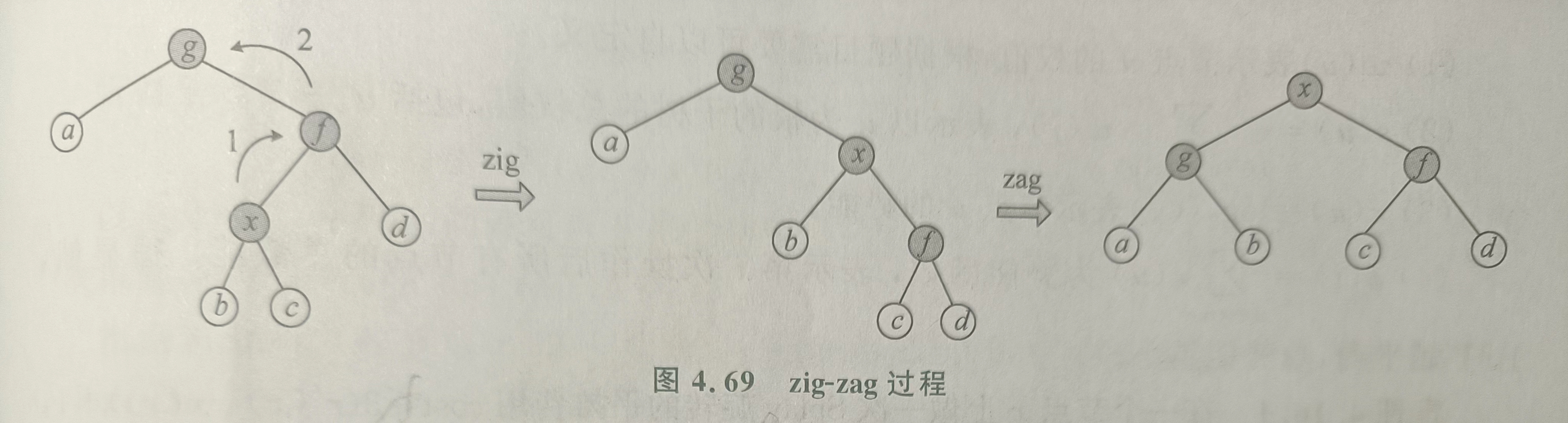
不能先旋转 \(f\) 再旋转 \(u\),否则在旋转 \(f\) 时,\(u\) 的深度不会改变。
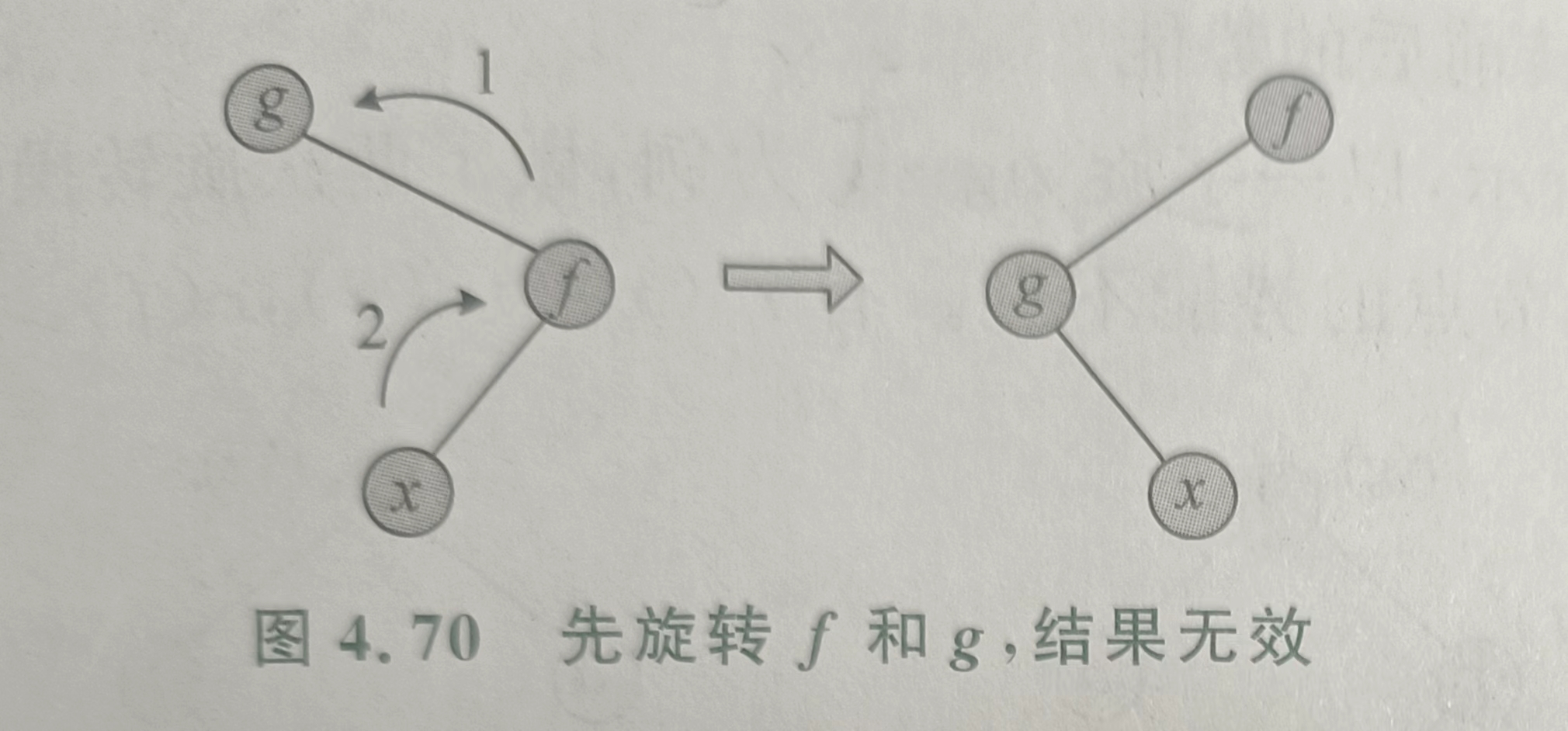
可以证明,Splay 树的时间复杂度平摊后为 \(\mathcal{O}(\log N)\),效率很高。证明参考这里。
2. 常用操作和代码
Splay 树可以处理区间问题。若要处理 \([l,r]\) 的区间,方法如下:
-
将结点 \(l-1\) 旋转到根。
-
将结点 \(r+1\) 旋转到 \(l-1\) 的儿子。
此时结点 \(r+1\) 的左儿子即为需要操作的区间。
每个结点需要记录的信息有父亲、左儿子、右儿子、子树大小以及结点的值。
设 \(u\) 为 \(f\) 的左儿子,\(x\) 为 \(u\) 的右儿子,\(g\) 为 \(f\) 的父亲。旋转前的形态如下图:
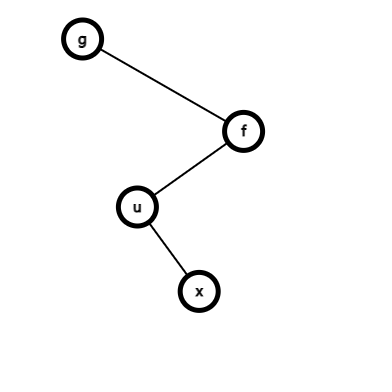
旋转后的形态如下图:
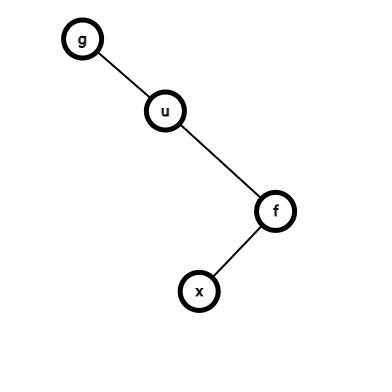
因此要更新的部分主要有下面几个:
\(x\) 的父亲、\(f\) 的左儿子、\(f\) 的父亲、\(u\) 的右儿子、\(u\) 的父亲、\(g\) 的其中一个儿子。
在处理区间问题时,我们需要先找到结点 \(l-1\) 与 \(r+1\)。这与普通平衡树的查询第 \(k\) 小数的代码差不多,但这里返回的是节点编号。代码如下:
node* fd(int k){
node *u=root;
while(k!=u->ls->sz+1){
if(k<u->ls->sz+1){
/*第k小在左子树*/
u=u->ls;
}else{
/*在右子树*/
k-=u->ls->sz+1;
u=u->rs;
}
}
return u;
}
我们可以先写一个函数判断一个结点是左儿子还是右儿子。代码如下:
bool ls(node *u){
return u->fa->ls==u;
/*如果u是左儿子,返回true*/
}
因此单旋操作的代码如下。
void rtt(node *u){
node *f=u->fa,*g=f->fa;
if(ls(u)){
/*zig操作*/
f->ls=u->rs;
/*更新f的左儿子*/
if(f->ls!=t){
/*f有左儿子,更新它的父亲*/
f->ls->fa=f;
}
u->rs=f;
}else{
/*zag操作同理*/
f->rs=u->ls;
if(f->rs->fa!=t){
f->rs->fa=f;
}
u->ls=f;
}
if(g!=t){
/*更新g的儿子*/
ls(f)?g->ls=u:g->rs=u;
}else{
/*u没有祖父,说明u的父亲为根,那么旋转后u就为根*/
root=u;
}
f->fa=u;u->fa=g;
push_up(f);push_up(u);
/*不要忘记push_up*/
}
Splay 树的主要操作是将一个结点旋转至根或另一个节点的儿子,通过不断的旋转完成。代码如下:
void splay(node *u,node *p){
/*如果p=t,将u旋转至根,否则旋转至p的儿子*/
node *f,*g;
while(u->fa!=p){
f=u->fa;g=f->fa;
/*父亲与祖父*/
if(g!=p){
/*u离p至少还有两层,做双旋*/
rtt(ls(u)^ls(f)?u:f);
/*ls(u)^ls(f)说明不在同一直线,先转u,否则先转f*/
}
rtt(u);
/*不管单旋,一字旋还是之字旋,最后一次都是旋转u*/
}
}
在操作的时候,如果初始时是空树,那么在找 \(l-1,r+1\) 时会出错。因此通常先设结点 \(1\) 为根,结点 \(2\) 为 \(1\) 的右儿子,后面对结点 \(2\) 的左儿子操作,且区间都向后移一位。
下面给出例题和代码。
本题可以用 Splay 树实现。
Splay 不能直接用做权值平衡树,需要再进行一些修改。



