AtCoder-abc340_f 题解
题意简述
给定整数 \(x,y\),询问是否存在整数 \(a,b\),满足:
-
\(-10^{18} \le a,b \le 10^{18}\)。
-
由 \((0,0),(x,y),(a,b)\) 三点构成的三角形面积为 \(1\)。
如果存在,输出任意一组;否则输出 -1。
思路
先假设 \(x,y,a,b\) 都是正数。那么图大概是这样:
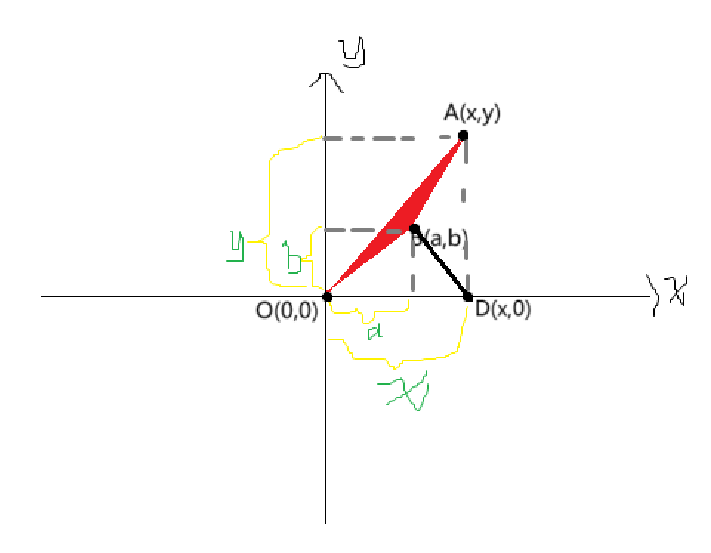
此时红色三角形的面积就是 \(S_{\triangle ADO}-S_{\triangle OBD}-S_{\triangle ABD}=\frac{xy}{2}-\frac{xb}{2}-\frac{(x-a)y}{2}=\frac{xy-xb-xy+ay}{2}=\frac{ay-xb}{2}=1\)。
\(\therefore ay-xb=2\),即 \(ya+(-x)b=2\)。
这是一个形如 \(ax+by=c\) 的二元线性丢番图方程。设 \(g=\gcd(a,b)\)。根据裴蜀定理,当 \(2\) 是 \(g\) 的倍数时,该方程有解。因此无解的条件就是 \(g>2\)。
接下来可以用扩展欧几里得算法求解。
欧几里得算法:
\(\gcd(a,b)=\gcd(b,a \bmod b)\)。若 \(b=0\),则 \(\gcd(a,b)=a\)。
扩展欧几里得算法:
先来解 \(ax+by=g\)。
以样例 \((3,5)\) 为例。将求 \(\gcd(3,5)\) 迭代过程展现出来,就是这样:
| a | b |
|---|---|
| \(3\) | \(5\) |
| \(5\) | \(3\) |
| \(3\) | \(2\) |
| \(2\) | \(1\) |
| \(1\) | \(0\) |
最后 \(a=1,b=0\),此时 \(x=1,y=0\) 就是一组合法的解。
能否根据最后一层的解不断往上求呢?
设倒数第二层的数为 \(a,b\),解为 \(x^{\prime},y^{\prime}\);最后一层的数为 \(b,a \bmod b\),解为 \(x,y\)。则有:
\(ax^{\prime}+by^{\prime}=1,bx+(a \bmod b)y=1\)。
由被除数 \(=\) 除数 \(\times\) 商 \(+\) 余数可知:余数 \(=\) 被除数 \(-\) 除数 \(\times\) 商。
\(\therefore a \bmod b=a-\lfloor \frac{a}{b} \rfloor \times b\)
\(\therefore bx+(a-\lfloor \frac{a}{b} \rfloor b)y=1\)
乘法分配:
\(\therefore bx+ay-\lfloor \frac{a}{b} \rfloor by=1\)
变形一下:
\(\therefore ay+bx-\lfloor \frac{a}{b} \rfloor by=1\)
因式分解,提出 \(b\):
\(\therefore ay+b(x-\lfloor \frac{a}{b} \rfloor y)=1\)
到这个时候就已经做出来了,因为 \(x^{\prime}\) 变成了 \(y\),\(y^{\prime}\) 变成了 \(x-\lfloor \frac{a}{b} \rfloor y\)。
我们可以写一个 exgcd 函数,在求解 \(\gcd(a,b)\) 的同时返回一组 \(ax+by=1\) 的解。但是此时有三个返回值,这个时候我们可以传址调用。
函数如下。
ll exgcd(ll a,ll b,ll &x,ll &y){
/*返回gcd(a,b),以及ax+by=gcd(a,b)的解x,y*/
if(!b){
/*b=0,则gcd(a,b)=1,同时x=1,y=0是一组解*/
x=1;y=0;return a;
}
ll g=exgcd(b,a%b,x,y),t;
t=x;
x=y;
y=t-a/b*y;
return g;
}
我们还可以在迭代的时候就交换 \(x,y\),这样就不用再声明 \(t\) 了。函数如下。
ll exgcd(ll a,ll b,ll &x,ll &y){
/*返回gcd(a,b),以及ax+by=gcd(a,b)的解x,y*/
if(!b){
/*b=0,则gcd(a,b)=1,同时x=1,y=0是一组解*/
x=1;y=0;return a;
}
ll g=exgcd(b,a%b,y,x);
/*在这里直接交换x,y*/
y-=a/b*x;
return g;
}
这样求解出来后,只是 \(ax+by=g\) 的解。要想求出 \(ax+by=2\) 的解,只需将两边同乘 \(\frac{2}{g}\) 即可。
那么正负号的问题呢:
exgcd 函数是不能接受负数的,因此应该把绝对值传进去。
原来是 \(ya+(-x)b=2\),现在是 \(\lvert y \rvert a+\lvert -x \rvert b=2\)。如果 \(x,y\) 传入的是 \(-x,-y\),根据负负得正,只需要把 \(a,b\) 对应的变为 \(-a,-b\) 即可。如果 \(y<0\),那么 \(\lvert y \rvert=-y\),此时 \(a\) 应该变为 \(-a\)。如果 \(x>0\),那么 \(\lvert -x \rvert=x\),此时 \(b\) 应该变为 \(-b\)。那么这道题就做出来了。



