分块与莫队算法
1. 分块
分块的思想
分块是把一个长度为 \(N\) 的数列分为 \(\sqrt{N}\) 个块,每个块的长度为 \(\sqrt{N}\)。这样在区间操作的时候,对于每个涉及到的块,如果涉及到半个块,就直接操作;如果涉及到整个块,就整体操作。
下面通过例题来了解一下分块。
这道题可以用分块来做。
先把序列分为 \(\sqrt{N}\) 个块,用 \(sqr\) 表示块的数量,\(sum_i\) 表示第 \(i\) 个块中所有数的和,\(add_i\) 表示第 \(i\) 个块中所有标记的总和,\(len_i\) 表示第 \(i\) 个块的大小。
- 区间修改
先判断 \(x,y\) 是否在同一个块,如果是就直接求和并输出。
否则再判断 \(x\) 是否为所在块的左端点,如果不是,就把这个块中 \(x\) 及其右边的数都直接加上 \(k\),并把 \(x\) 移动到下一个块。\(y\) 的移动同理。
接下来把 \(x,y\) 所在块中间的块的标记都加上 \(k\) 即可。
- 区间查询
原理和区间修改相同。只不过在加整块的时候,需要加的是 \(add_i \times len_i\)
这样总时间复杂度为 \(\mathcal{O}(M \sqrt{N})\),可以通过此题。
和 例1 类似,区间标记可以参考线段树。
2. 基础莫队算法
基础莫队思想
基础莫队算法是一种离线算法。它适用于只查询不修改的区间问题。
基础莫队算法是基于分块的。它一般将所有操作读入后,按照块排序,然后处理并输出。
下面根据例题来理解一下基础莫队算法。
下面给出不同的解法。
- 扫描法
定义两个指针 \(L,R\),用 \(cnt_i\) 表示区间 \([L,R]\) 中每个数的出现次数。两个指针可以移动。当 \(L\) 左移或 \(R\) 右移时,区间中会加入一个数;当 \(L\) 右移或 \(R\) 左移时,区间中会减少一个数。设 \(ans\) 表示此时区间中不同数的个数。加入后,如果这个数的出现次数为 \(1\),则让 \(ans \leftarrow and+1\)。减少后,如果这个数的出现次数为 \(0\),则让 \(ans \leftarrow ans-1\)。
这样可以对所有查询按左端点排序,每次通过移动指针来查询。这样的时间复杂度最差为 \(\mathcal{O}(NQ)\),不能通过。
- 基础莫队算法
基础莫队算法先将序列分块,然后将所有操作按左端点的块来排序,如果左端点的块相同,再按右端点排序。
这样看起来其实没啥优化,但是下图可以充分体现效果。用 \(L\) 表示横坐标,\(R\) 表示纵坐标,所有线段的长度即为两个指针移动的距离。
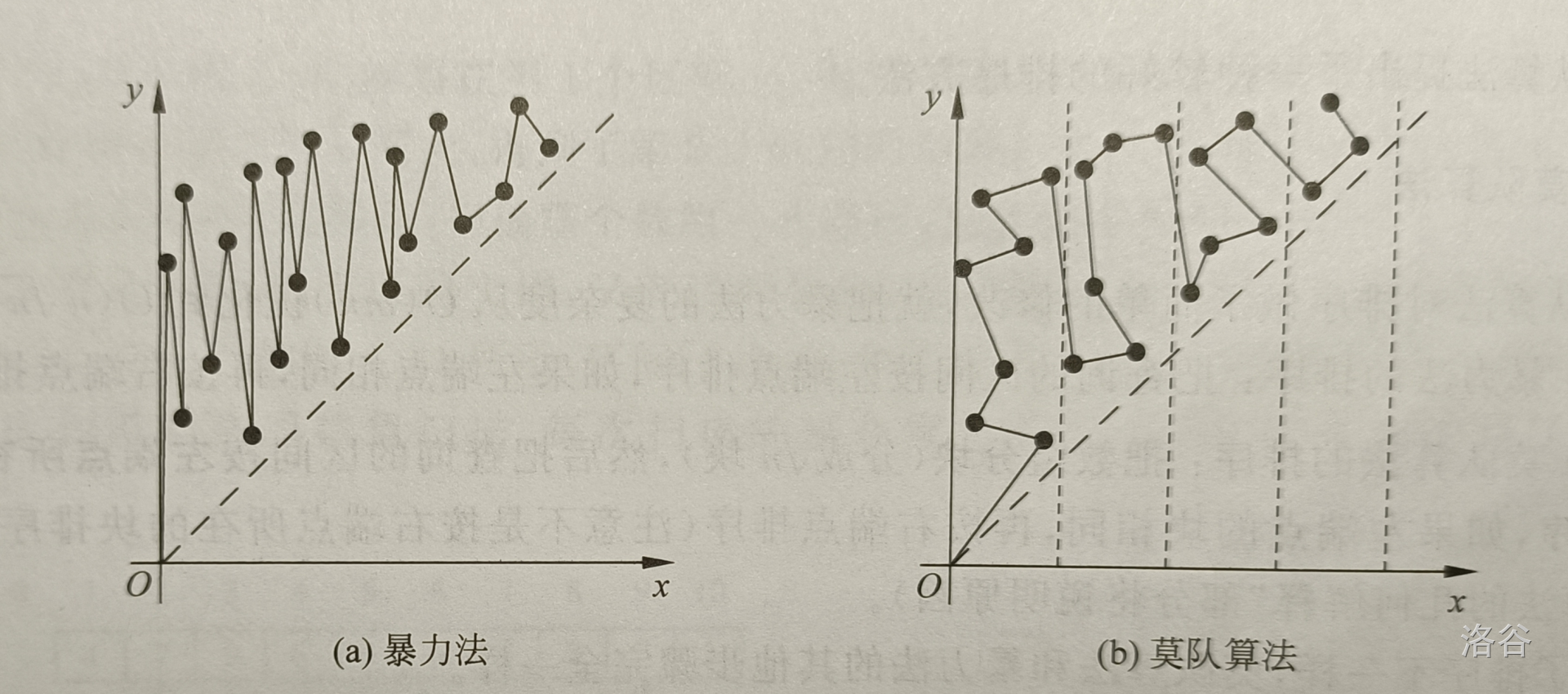
这样所有 \(\sqrt{N}\) 个块中,\(L\) 最多移动 \(Q \sqrt{N}\) 次,\(R\) 最多移动 \(Q \sqrt{N}\) 次。所以总时间复杂度为 \(\mathcal{O}(Q \sqrt{N})\),可以通过此题。



