树状数组 算法笔记
已知一个长度为 \(n\) 的序列 \(a\)，共有 \(m\) 次操作，每次操作如下：
- 将某一个数加上 \(x\)。
- 求出某区间的和。
对于这个题目，有多种方式求解，例如：
- 暴力求解，时间复杂度 \(O(mn)\)。
- 前缀和求解，由于前缀和不好进行修改，时间复杂度也是 \(O(mn)\)。
- 差分求解，由于需要统计区间和，时间复杂度 \(O(mn)\)。
对于这个题目，我们不好用上述方法求解，我们引入一个新的算法：树状数组。
现在有一个区间 \([1,x]\)，现在要求出这个区间的和，我们可以将 \(x\) 进行二进制分解，也就可以将 \([1,x]\) 这个区间转化成若干个区间长度为 \(2\) 的幂的区间的和：
- \([1,2^{i_0}]\) 长度为 \(2^{i_0}\)。
- \([1+2^{i_0},2^{i_0}+2^{i_1}]\) 长度为 \(2^{i_1}\)。
- \([1+2^{i_0}+2^{i_1},2^{i_0}+2^{i_1}+2^{i_2}]\) 长度为 \(2^{i_2}\)
- \(\dots\)
其中 \(i_0>i_1>i_2>\dots>i_k<\log_2x\)。
定义 \(\text{lowbit}(x)\) 为 \(x\) 二进制分解后的最低位的 \(1\)。
\(\text{lowbit(3)}=1,\text{lowbit(12)}=4\)
设上面的区间和为 \(c_i=\sum_{j=i-\text{lowbit}(i)}^{i}{a_j}\)，表示图如下。
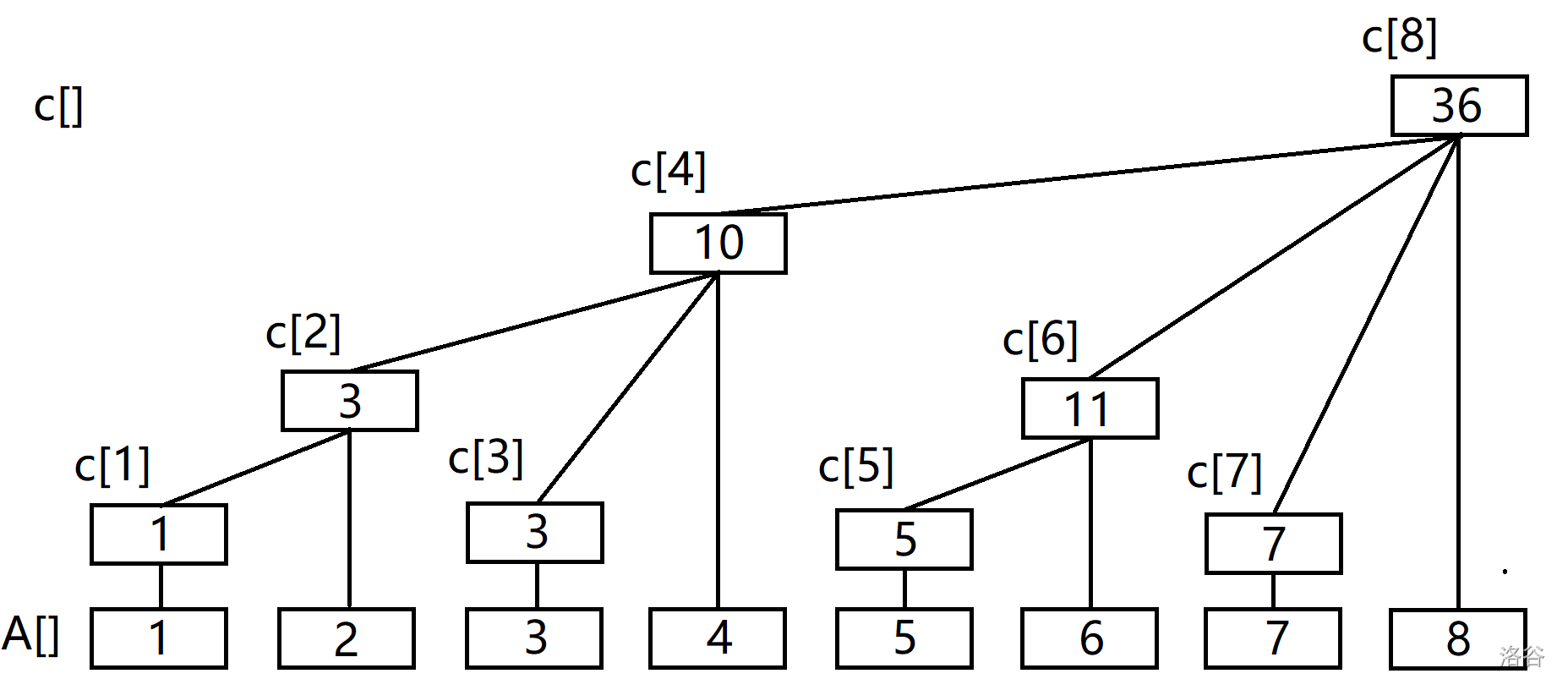
假设我们可以预处理出区间长度为 \(2\) 的幂的区间和，那么对于每一次遍历，先遍历长度最小的区间加上他的区间和，长度为 \(\text{lowbit}(x)\)，每一次将 \(x\) 减去 \(\text{lowbit}(x)\)，知道 \(x\) 的值为 \(0\) 为值即可。
于是查询区间 \([1,x]\) 的代码便出来了：
LL query(int x) {
LL ret = 0;
for (int i = x; i; i -= lowbit(i)) {
ret += c[i];
}
return ret;
}
查询区间 \([l,r]\) 做一次前缀和就可以了。
然而单点修改 \(a_x\) 加上 \(k\)，我们先仔细观察上面的 \(c\) 数组的图片试试。
如果将 \(a_2\) 加上 \(3\) 那么 \(c_2\) 要加上 \(3\)，你会发现 \(c_4\) 也要加上 \(3\)，\(c_8\) 也要加上 \(3\)，你会发现如果 \(c\) 数组是以 \(c_n\) 为根节点的树的话，那么 \(c_i\) 的父亲节点就是 \(c_{i+\text{lowbit}(i)}\) 且 \(c_{i+\text{lowbit}(i)}\) 的区间一定会包含 \(c_i\) 且其他的区间一定不会包含 \(c_i\) 因为这是一颗树。
若要将 \(c_x\) 加上 \(k\)，就是将 \(c_x\) 的上面一个节点的 \(c_{x+\text{lowbit}(x)}\)，也就是他的父亲节点的权值，也加上 \(k\) 即可，然后让 \(c_{x+\text{lowbit}(x)}\) 的父亲节点也加上 \(k\) 即可。
代码如下：
void update(int x, int y) {
for (int i = x; i <= n; i += lowbit(i)) {
c[i] += y;
}
}
我们先在就是要求 \(\text{lowbit}(x)\)，我们不妨将 \(x\) 取反，然后将 \(x\) 加 \(1\)，你会发现 \(x\) 的最后一个 \(1\) 的位置到最后没有变化，但是前面的全部取反，将原数 \(x\) 与上现在的数，就求出了 \(\text{lowbit}(x)\) 了。
我们知道负数补码的操作就是将一个数取反后加一，于是就可以简化成这样：
int lowbit(int x) { return x & -x; }
初始化树状数组就是在每一次加入元素中将这个元素加上这个值即可，时间复杂度：\(O(n\log_2n)\)。
另一种方法就是考虑动态规划加入每一个节点时将其所有的祖宗节点全部加上它的值即可，时间复杂度：\(O(n)\)。
void build() {
for (int i = 1; i <= n; i++) {
c[i] = a[i];
}
for (int i = 1; i <= n; i++) {
if (i + lowbit(i) <= n) {
c[i + lowbit(i)] += c[i];
}
}
}
由于在 \(m\) 次询问中也会出现 \(O(m\log_2n)\) 的时间复杂度，用 \(O(n\log_2n)\) 的初始化方法更加简洁。
所以上面的代码就出来了：
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int kMaxN = 5e5 + 5;
int n, m, a[kMaxN], opt, x, y;
LL c[kMaxN];
int lowbit(int x) { return x & -x; }
void update(int x, int y) {
for (int i = x; i <= n; i += lowbit(i)) {
c[i] += y;
}
}
LL query(int x) {
LL ret = 0;
for (int i = x; i; i -= lowbit(i)) {
ret += c[i];
}
return ret;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> a[i];
update(i, a[i]);
}
while (m--) {
cin >> opt >> x >> y;
if (opt == 1) {
update(x, y);
} else {
cout << query(y) - query(x - 1) << "\n";
}
}
return 0;
}
由此发现，普通树状数组维护的区间必须满足以下特征：
- 结合律：\((x\circ y)\circ z=x\circ(y\circ z)\)，其中 \(\circ\) 是一个二元运算符。
- 可差分：具有逆运算的运算，即已知 \(x\circ y\) 和 \(x\) 可求出 \(y\)。
已知一个数列，你需要进行下面两种操作：
- 某区间每一个数加上 \(x\)；
- 某一个数的值。
这道题考虑用树状数组求解。仔细观察两种操作，第一种操作“每个区间每一个数加上 \(x\)”这个操作十分像差分，其实我们可以用树状数组维护差分数组即可。
代码如下：
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int kMaxN = 5e5 + 5;
int n, m, a[kMaxN], opt, x, y, k;
LL c[kMaxN];
int lowbit(int x) { return x & -x; }
void update(int x, int y) {
for (int i = x; i <= n; i += lowbit(i)) {
c[i] += y;
}
}
LL query(int x) {
LL ret = 0;
for (int i = x; i; i -= lowbit(i)) {
ret += c[i];
}
return ret;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> a[i];
update(i, a[i] - a[i - 1]);
}
while (m--) {
cin >> opt;
if (opt == 1) {
cin >> x >> y >> k;
update(x, k), update(y + 1, -k);
} else {
cin >> x;
cout << query(x) << "\n";
}
}
return 0;
}
