【NOIP2020】移球游戏 - 分治

题目描述

小 C 正在玩一个移球游戏，他面前有 \(n+1\) 根柱子，柱子从 \(1 \sim n + 1\) 编号，其中 \(1\) 号柱子、\(2\) 号柱子、……、\(n\) 号柱子上各有 \(m\) 个球，它们自底向上放置在柱子上，\(n + 1\) 号柱子上初始时没有球。这 \(n \times m\) 个球共有 \(n\) 种颜色，每种颜色的球各 \(m\) 个。

初始时一根柱子上的球可能是五颜六色的，而小 C 的任务是将所有同种颜色的球移到同一根柱子上，这是唯一的目标，而每种颜色的球最后放置在哪根柱子则没有限制。

小 C 可以通过若干次操作完成这个目标，一次操作能将一个球从一根柱子移到另一根柱子上。更具体地，将 \(x\) 号柱子上的球移动到 \(y\) 号柱子上的要求为：

1. \(x\) 号柱子上至少有一个球；
2. \(y\) 号柱子上至多有 \(m - 1\) 个球；
3. 只能将 \(x\) 号柱子最上方的球移到 \(y\) 号柱子的最上方。

小 C 的目标并不难完成，因此他决定给自己加加难度：在完成目标的基础上，使用的操作次数不能超过 \(820000\)。换句话说，小 C 需要使用至多 \(820000\) 次操作完成目标。

小 C 被难住了，但他相信难不倒你，请你给出一个操作方案完成小 C 的目标。

思路

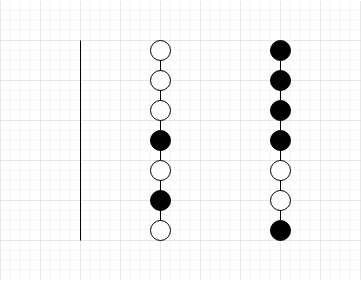
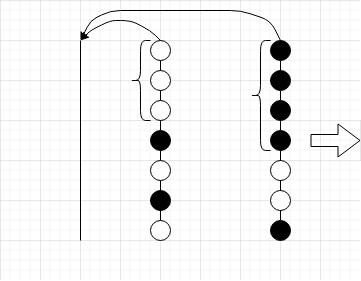
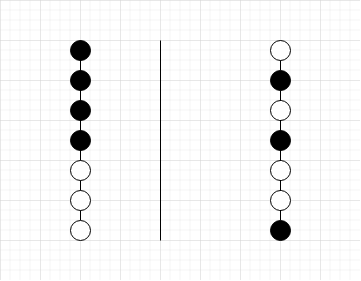
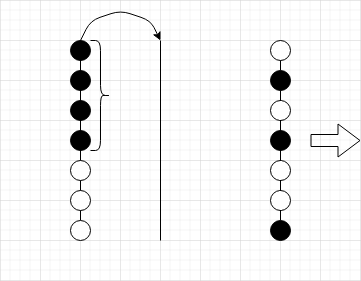
首先若只有两个颜色的球，可以用如下 gif 演示的方案用空柱子分离

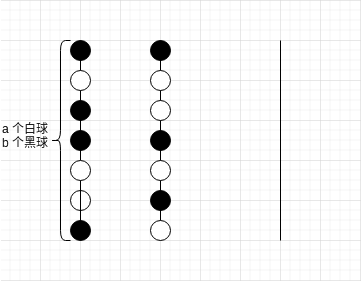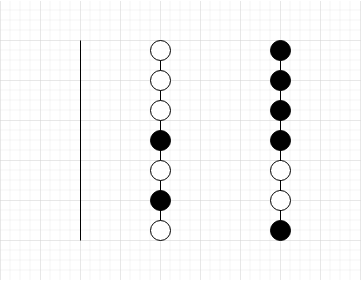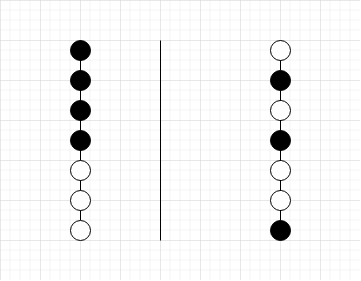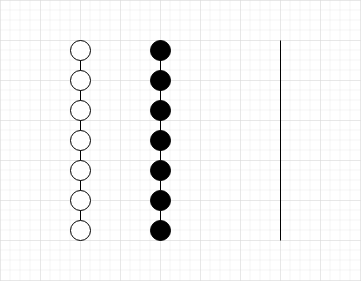
具体过如下：

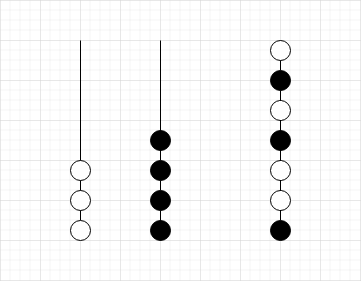
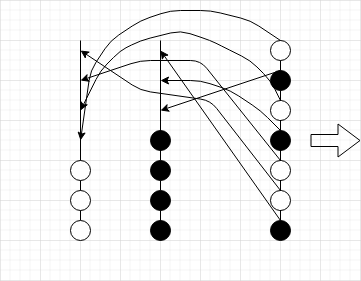
有 \(a\) 个白球与 \(b\) 个黑球

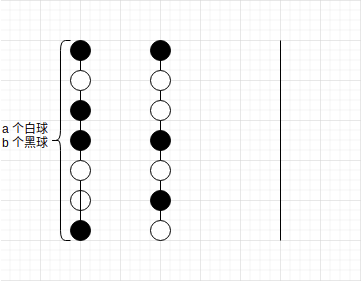
1.将第二个柱腾出 \(a\) 个空位

2.分离第一个柱子的黑白球 3.放回第一个柱子 4.腾出第二个柱子 5.把第一个柱子的黑球放到第二个柱子 6.分离第三个柱子

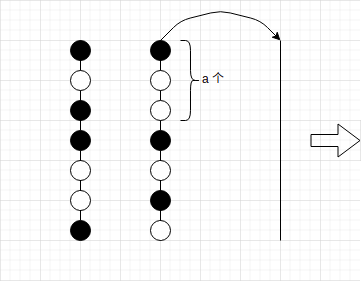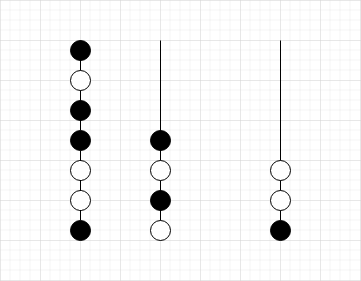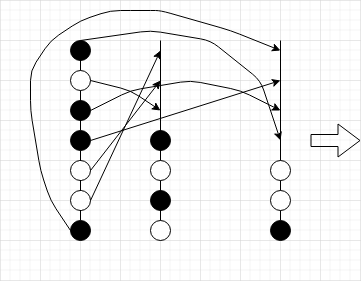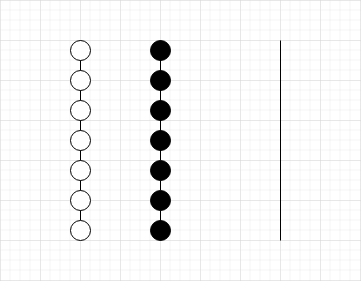此方案的移动次数为 \(5m-a\)

所以得到了多个颜色的做法：分治求解区间 \([l,r]\) 的柱子，设一个阀值 \(mid=\frac{l+r}{2}\)，将小于等于 \(x\) 的数和大于 \(x\) 的数视作两个颜色，枚举 \([l,mid]\) 和 \([mid+1,r]\) 两个柱子，按照上述方法分离两种颜色的球，再分治求解两个子区间.

注意到枚举的两根柱子两种颜色数量不一定相等，于是就只还原多的那种颜色的柱子.

操作次数看成 \(5m\)，总的操作次数则是 \(T(n)=2T(\frac{n}{2})+5mn=5mn\log n\le 820000\)

#include <utility>
#include <cstring>
#include <cstdio>
using namespace std;
const int maxn = 400 + 10;
int n,m,tot,pos[maxn][maxn];
pair<int,int> ans[820001];
bool fin[maxn];
inline void move(int x,int y) {
	ans[++tot] = make_pair(x,y);
	pos[y][++pos[y][0]] = pos[x][pos[x][0]--];
}
inline void solve(int l,int r) {
	if (l == r) return;
	int mid = l+r>>1;
	memset(fin,false,sizeof fin);
	for (int i = l;i <= mid;i++)
		for (int j = mid+1;j <= r;j++) if (!fin[i] && !fin[j]) {
			int s = 0,cnt = 0;
			for (int k = 1;k <= m;k++) s += (pos[i][k] <= mid)+(pos[j][k] <= mid);
			int a = (s >= m ? i : j),b = (s >= m ? j : i);
			for (int k = 1;k <= m;k++)
				if (s >= m) cnt += pos[a][k] <= mid;
				else cnt += pos[a][k] > mid;
			for (int k = 1;k <= cnt;k++) move(b,n+1);
			for (int k = m;k >= 1;k--)
				if (s >= m) move(a,pos[a][k] <= mid ? b : n+1);
				else move(a,pos[a][k] > mid ? b : n+1);
			for (int k = 1;k <= cnt;k++) move(b,a);
			for (int k = 1;k <= m-cnt;k++) move(n+1,a);
			for (int k = 1;k <= m-cnt;k++) move(b,n+1);
			for (int k = 1;k <= m-cnt;k++) move(a,b);
			for (int k = m;k >= 1;k--)
				if (s >= m) move(n+1,pos[a][0] < m && pos[n+1][k] <= mid ? a : b);
				else move(n+1,pos[a][0] < m && pos[n+1][k] > mid ? a : b);
			fin[a] = true;
		}
	solve(l,mid);
	solve(mid+1,r);
}
int main() {
	scanf("%d%d",&n,&m);
	for (int i = 1;i <= n;i++) {
		pos[i][0] = m;
		for (int j = 1;j <= m;j++) scanf("%d",&pos[i][j]);
	}
	solve(1,n);
	printf("%d\n",tot);
	for (int i = 1;i <= tot;i++) printf("%d %d\n",ans[i].first,ans[i].second);
	return 0;
}