【CF238C】World Eater Brothers - 树形 DP

题目描述

You must have heard of the two brothers dreaming of ruling the world. With all their previous plans failed, this time they decided to cooperate with each other in order to rule the world.

As you know there are \(n\) countries in the world. These countries are connected by \(n-1\) directed roads. If you don't consider direction of the roads there is a unique path between every pair of countries in the world, passing through each road at most once.

Each of the brothers wants to establish his reign in some country, then it's possible for him to control the countries that can be reached from his country using directed roads.

The brothers can rule the world if there exists at most two countries for brothers to choose (and establish their reign in these countries) so that any other country is under control of at least one of them. In order to make this possible they want to change the direction of minimum number of roads. Your task is to calculate this minimum number of roads.

题目大意

给出一个 \(n\) 个点，\(n-1\) 条边的有向图

求最少翻转多少条边的方向，使得入度为 \(0\) 的点最多有两个

思路

入度为零的若只有一个，答案就是 \(0\)，否则翻转成两个入度为零的一定一个的答案优

然后两个入度为零的目标图的如下，两个点的出边最终汇聚在一个点

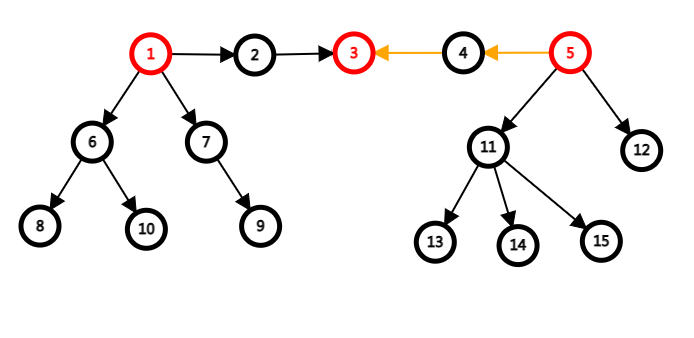
若此图以其中一个入度为零的点为根，那么除了汇聚点到另一个入度为零的点这段路径上的边，是由儿子指向父亲的，其他所有的边都是由父亲指向儿子的

所以先枚举一个点作为其中一个入度为零的点，然后统计所有儿子指向父亲的边有多少条，记为 \(cnt\)

然而此时汇聚点到另一个入度上的边的情况是反的，它需要翻转的是父亲指向儿子的边

所以记这条路径上，父亲指向儿子的边个数为 \(A\)，儿子指向父亲的边个数为 \(B\)，答案即为 \(cnt+A-B\)

想要答案最小，就要最大化 \(B-A\)，设 \(f_i\) 为以点 \(i\) 为汇聚点，其到子树中的一个点路径上的 \(B-A\)

所以 \(f_i=min_{s \in son(i)}\{f[s]+w\}\)，其中，若此边是儿子到父亲 \(w=1\)，否则 \(w=-1\)

#include <algorithm>
#include <utility>
#include <vector>
#include <cstdio>
using namespace std;
const int maxn = 3000 + 10;
vector<pair<int,int> > edge[maxn];
int n,cnt,ans(maxn),f[maxn];
inline void dfs(int now,int fa) {
	f[now] = 0;
	for (size_t i = 0;i < edge[now].size();i++) {
		int to = edge[now][i].first,w = edge[now][i].second;
		if (to ^ fa) {
			dfs(to,now);
			cnt += w;
			f[now] = max(f[now],f[to]+(w ? 1 : -1));
		}
	}
}
int main() {
	scanf("%d",&n);
	for (int i = 1,u,v;i < n;i++) {
		scanf("%d%d",&u,&v);
		edge[u].push_back(make_pair(v,0));
		edge[v].push_back(make_pair(u,1));
	}
	for (int i = 1;i <= n;i++) {
		dfs(i,cnt = 0);
		ans = min(ans,cnt-*max_element(f+1,f+n+1));
	}
	printf("%d",ans);
	return 0;
}