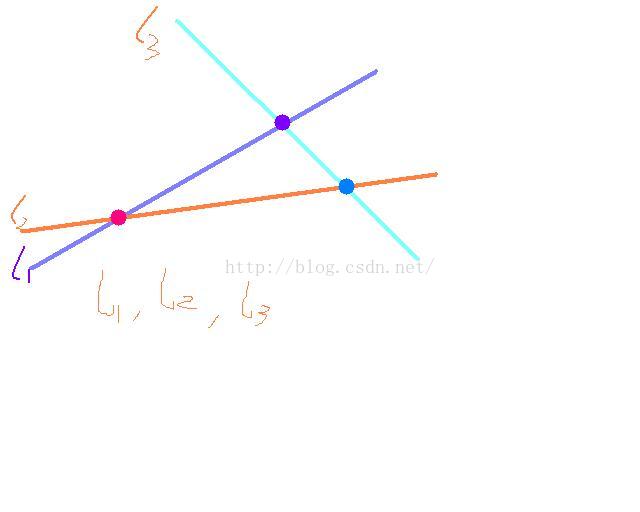【bzoj 1007】[HNOI2008]水平可见直线（计算几何）

1007: [HNOI2008]水平可见直线

Time Limit: 1 Sec  Memory Limit: 162 MB
Submit: 5509  Solved: 2082
[Submit][Status][Discuss]

Description

　　在xoy直角坐标平面上有n条直线L1,L2,...Ln,若在y值为正无穷大处往下看,能见到Li的某个子线段,则称Li为
可见的,否则Li为被覆盖的.
例如,对于直线:
L1:y=x; L2:y=-x; L3:y=0
则L1和L2是可见的,L3是被覆盖的.
给出n条直线,表示成y=Ax+B的形式(|A|,|B|<=500000),且n条直线两两不重合.求出所有可见的直线.

Input

　　第一行为N(0 < N < 50000),接下来的N行输入Ai,Bi

Output

　　从小到大输出可见直线的编号，两两中间用空格隔开,最后一个数字后面也必须有个空格

Sample Input

3
-1 0
1 0
0 0

Sample Output

1 2

HINT

Source

[Submit][Status][Discuss]

【题解】【计算几何】

【如图，将所有直线按斜率降序排列，然后按照斜率优化类似的方法进行查询，用栈维护】

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
struct data{
	int k,b,num;
};
data a[50010],que[50010];
int n,tail;
bool ans[50010];
int tmp(data x,data y)
{
	return x.k>y.k;
}
inline bool check(data x1,data x2,data x3)
{
	ll s1=(ll)(x1.k-x3.k)*(ll)(x2.b-x1.b);
	ll s2=(ll)(x1.k-x2.k)*(ll)(x3.b-x1.b);
	return s1>=s2;
}
int main()
{
	int i,j;
	scanf("%d",&n);
	for(i=1;i<=n;++i)
	 scanf("%d%d",&a[i].k,&a[i].b),a[i].num=i;
	sort(a+1,a+n+1,tmp); 
	tail=0;
	for(i=1;i<=n;++i)
	 {
	 	while(tail>1&&(check(que[tail],que[tail-1],a[i])||que[tail].k==a[i].k&&a[i].b>que[tail].b))//满足条件的都会被遮挡，所以无法看到
	 	  ans[que[tail].num]=0,tail--;
	 	tail++; que[tail]=a[i]; ans[a[i].num]=1;
	 }
	for(i=1;i<=n;++i)
	 if(ans[i]) printf("%d ",i);
	return 0;
}