【bzoj 2393】Cirno的完美算数教室(容斥原理)
2393: Cirno的完美算数教室
Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 304 Solved: 187
[Submit][Status][Discuss]
Description
~Cirno发现了一种baka数,这种数呢~只含有2和⑨两种数字~~
现在Cirno想知道~一个区间中~~有多少个数能被baka数整除~
但是Cirno这么天才的妖精才不屑去数啦
只能依靠聪明的你咯。
Input
一行正整数L R
( 1 < L < R < 10^10)
Output
一个正整数,代表所求的答案
Sample Input
1 100
Sample Output
58
HINT
Source
【题解】【容斥原理】
首先预处理出1~r以内所有只由2和9构成的baka数 容易发现最多有1022个
但是其中有一些baka数是另一些的倍数 比如说a是b的倍数 那么一个数如果是a的倍数那么就一定是b的倍数 我们只需要计算b即可 无需计算a 这里可以把所有满足条件的a剔除掉,剔除后最多应该有500左右,求区间内这些数的倍数的数的数量 可以开始容斥了
总数=是一个数的倍数的数的数量-是两个数公倍数的数的数量+是三个数公倍数的数的数量……
比如说枚举到某n个数的公倍数 就是对这n个数做一下LCM,然后利用容斥原理将r/lcm-(l-1)/lcm 计入答案
但是2^466枚举显然是不可能的 我们发现这466个数大多都比较大 ,很快就会超过10^10,所以搜索+减枝(特判只要大小超过上限就加入与之有关的数据然后返回上一层)即可。
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
ll a[10010],b[10010],l,r,ans,tot,tt;
bool p[10010];
void get_gcd(ll x)
{
if(x>r) return;
if(x) a[++tot]=x;
get_gcd(x*10+2);
get_gcd(x*10+9);
return;
}//找寻0-r间所有的含2或9的数
ll gcd(ll x,ll y)
{
ll last=x%y;
while(last)
{
x=y; y=last; last=x%y;
}
return y;
}
void dfs(ll x,ll y,ll sum)
{
if(x>tt)
{
if(y&1) ans=ans+r/sum-(l-1)/sum;
else
if(y) ans=ans-r/sum+(l-1)/sum;//容斥原理的公式:+一个数的倍数-二个数的倍数+三个数的倍数……
return;
}
dfs(x+1,y,sum);
ll s=(sum*b[x])/(gcd(sum,b[x]));
if(s<=r) dfs(x+1,y+1,s);
return;
}
int main()
{
int i,j;
scanf("%lld%lld",&l,&r);
memset(p,true,sizeof(p));
get_gcd(0);
sort(a+1,a+tot+1);
for(i=1;i<=tot;++i)
if(p[i])
{
b[++tt]=a[i];
for(j=i;j<=tot;++j)
if(!(a[j]%a[i]))
p[j]=0;
} //筛出所有的不是别的数的倍数的数
dfs(1,0,1);
printf("%lld\n",ans);
return 0;
}
既然无能更改,又何必枉自寻烦忧


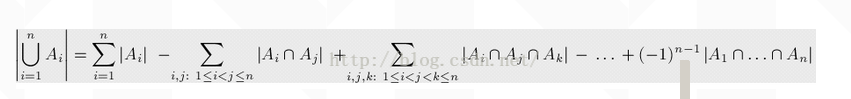

 浙公网安备 33010602011771号
浙公网安备 33010602011771号