树上分治

（借鉴漆子超的国家队论文：http://wenku.baidu.com/view/e087065f804d2b160b4ec0b5.html）

树的分治分为：树上点分治和树上边分治。

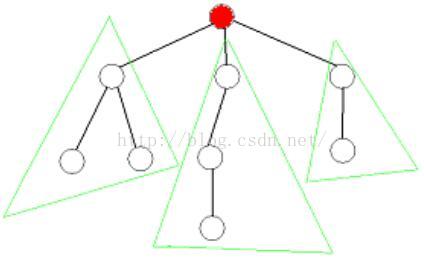
基于点的分治：首先选取一个点将无根树转为有根树，再递归处理每一颗以根结点的儿子为根的子树。

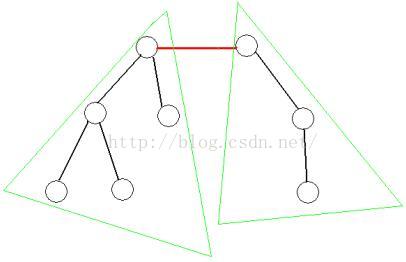
基于边的分治：在树中选取一条边，将原树分成两棵不相交的树，递归处理。

基于点的分治：我们选取一个点，要求将其删去后，结点最多的树的结点个数最小，这个点被称为“树的重心”。

基于边的分治：我们选取的边要满足所分离出来的两棵子树的结点个数尽量平均，这条边称为“中心边”

这两个问题，都可以使用在树上的动态规划来解决，时间复杂度均为O（N），其中N为树的结点总数。

两个定理（证明略）

 1）存在一个点使得分出的子树的结点个数均不大于N/2；

 2）如果一棵树中每个点的度均不大于D，那么存在一条边使得分出的两棵子树的结点个数在[N/(D+1),N*D/(D+1](N>=2)

 (由定理 1 可得，在基于点的分治中每次我们都会将树的结点个数减少一半，因此递归深度最坏是O(logN)，在树是一条链的时候达到上界。)

 （由定理 2 我们可以得到在D为常数时，基于边的分治递归最坏深度为O(logN)。）