【校内互侧】高维网络 （dp+组合数+容斥原理）

高维网络

【题目描述】
现在有一个 d 维的坐标网格，其中第 i 维坐标的范围是[0,a_i]。在这个范围内建立一个有向图：我们把范围内的每个整点（每一维坐标均为整数的点）当做图上的顶点。设点 A(0,0,⋯,0),B(a_1,a_2,⋯,a_d)。对于范围内的点(x_1,x_2,⋯,x_d)，它会向以下这些点（如果目标点在范围内）连有向边：(x_1+1,x_2,⋯,x_d),(x_1,x_2+1,⋯,x_d),⋯,(x_1,x_2,⋯,x_d+1)
现在从点 A 到点 B 会有若干条路径，路径的条数可以十分简单地算出。然而不幸的是，范围内有 p 个点被破坏了（点 A 和点 B 不会被破坏） ，其中第 i个点的坐标为(x_(i,1),x_(i,2),⋯,x_(i,d))。你需要算出从点 A 到点B 剩余的路径条数。
由于答案可能很大，你只需要输出它对 1,000,000,007 取模的结果。
【输入格式】
第一行为两个整数 d，p。
第二行为 d 个整数，其中第 i 个数是 a_i。
接下来 p 行，每行 d 个整数，其中第 i 行第 j 个数是 x_(i,j)。
【输出格式】
一个整数，表示从点 A 到点 B 剩余的路径条数对 1,000,000,007 取模的结果。
【输入样例】
2 1
2 1
1 0
【输出样例】
1
【数据范围】

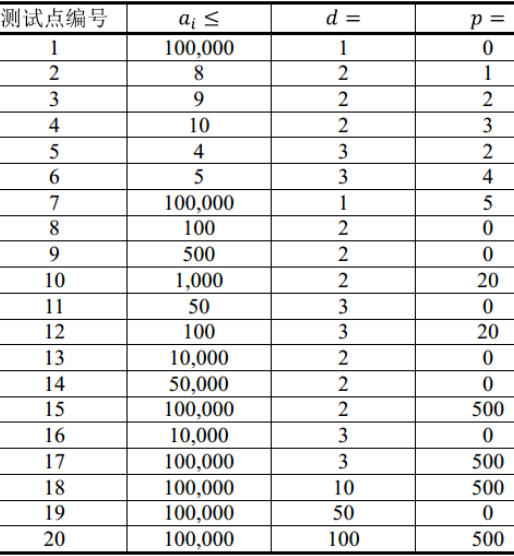
【题解】【dp+组合数+容斥原理】
【f[i]表示从A到i不经过被破坏的点的路径条数；g[i][j]表示从i到j可以经过的被破坏的点的方案数（可以用组合数求）】
【g[i][j]：（各维度权值之和的阶乘）/（各维度阶乘之积），如二维情况：（行数+列数）！/（行数！×列数！）】
【ｆ［ｉ］＝总路径条数－不合法，f[x]=g[A][x]-Σf[y]*g[y][x]】
【最后输出ｆ［Ｂ］】

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const int mod=1000000007;
struct bad{
    int x[110];
}a[510]; 
ll mi[10000010],sum[510],num[110],f[510],g[510][510],h[510];
int d,p;
int tmp(bad a,bad b)
{
    for(int i=1;i<=d;++i)
     {
        if(a.x[i]<b.x[i]) return 1;//刚开始写成 if(a.x[i]<b.x[i]) return 1; 
        if(a.x[i]>b.x[i]) return 0;  //           else return 0;  然后WA啊WA 
     }
} 
inline void jc()
{
    mi[0]=1;
    for(ll i=1;i<=10000000;++i)
     mi[i]=(ll)(mi[i-1]*i)%mod;
}
inline ll poww(ll x,ll num)
{
    ll ss=x%mod,ans=1;
    while(num)
     {
        if(num&1)
          ans=ans*ss%mod;
        num>>=1;
        ss=(ss*ss)%mod;
     }
    return ans%mod;
}
inline void slove()
{
    for(int i=1;i<=p;++i)
     {
        ll t=mi[sum[i]];
        ll t1=1;
        for(int j=1;j<=d;++j)
         if(a[i].x[j]) t1=(t1*mi[a[i].x[j]])%mod;
        ll ans=poww(t1,mod-2);
        g[0][i]=t*ans%mod;
     }
    for(int i=1;i<=p;++i)
     for(int j=1;j<=p;++j)
      if(i!=j)
       {
            ll tot=0; bool b=1;
            for(int k=1;k<=d;++k)
             {
                h[k]=a[j].x[k]-a[i].x[k],tot+=h[k];
                if(h[k]<0) {b=0; break;}
                }
            if(!b) continue;
            ll t=mi[tot],t1=1;
            for(int k=1;k<=d;++k)
             if(h[k]) t1=(t1*mi[h[k]])%mod;
            ll ans=poww(t1,mod-2);
            g[i][j]=t*ans%mod;
       }
    return;
}//预处理g[i][j] 
int main()
{
    freopen("cube.in","r",stdin);
    freopen("cube.out","w",stdout);
    int i,j;
    scanf("%d%d",&d,&p);
    for(i=1;i<=d;++i) scanf("%lld",&num[i]);
    for(i=1;i<=p;++i)
     for(j=1;j<=d;++j)
      scanf("%d",&a[i].x[j]);
    ++p;
    for(i=1;i<=d;++i) a[p].x[i]=num[i];
    sort(a+1,a+p+1,tmp);
    for(i=1;i<=p;++i)
     for(j=1;j<=d;++j)
      sum[i]+=a[i].x[j],sum[i]%=mod;
    jc();
    slove();
    for(i=1;i<=p;++i)
     {
        f[i]=g[0][i]%mod;
        for(j=1;j<i;++j)
         f[i]=(f[i]-f[j]*g[j][i])%mod;
        f[i]=(f[i]%mod+mod)%mod;
     }
    printf("%lld\n",f[p]);
    return 0;
}