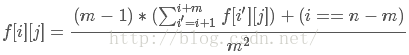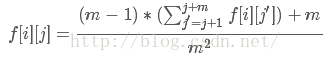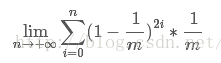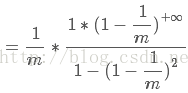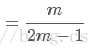【NOIP 模拟题】掷骰子(dp)
掷骰子(dice.cpp)
【问题描述】
太郎和一只兔子正在玩一个掷骰子的游戏。有一个N个格子的长条棋盘,太郎和兔子轮流掷一个M面的骰子,骰子M面分别是1到M的数字,且掷到每一面的概率是相同的,掷到几,就往前走几步,当谁走到第N格时,谁就获胜了。游戏中还有一个规则“反弹”,就是当一位选手走到N格外时,他就会后退(就像飞行棋进营一样)。
假设现在一位选手在A格,当他掷出B时:1)若A+B<N,走到A+B格;2)若A+B=N,走到第N格,获胜;3)若A+B>N,走到N-(A+B-N)格。
假设现在太郎和兔子分别在x格、y格,接下来是太郎掷骰子,太郎想知道他赢得比赛的概率是多少。
【问题输入】
一行4格整数N、M、x、y。
【问题输出】
一行一个小数,表示太郎获胜的概率(保留六位小数)
【样例输入】
10 6 1 1
【样例输出】
0.541725
【数据范围】
30%的数据:10<=N<=100;
100%的数据:10<=N<=2000,M,x,y<=n-1。
————————————————————————————————
【题解】【dp】
【f[i][j]表示A在第i格,B在第j格时,A获胜的概率。特别的:若i=n或j=n时,概率是1或0】
【分四种情况考虑:
[1)若i+m<=n、j+m<=n,即i、j都不能一步获胜]
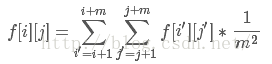
(A从走到i+1-i+m这之间的位置的可能性都是均等的,都是1/m,同理,B从走到j+1-j+m这之间的位置的可能性都是1/m,所以每一个f[i'][j']出现的概率都是1/(m²))
【2)i+m<=n、j+m>n [A不能一步到终点,B可能一步到终点]】
j只有1中可能上次从n转移过来,j共有m中取值;i也有m种取值,所以共有m²种可能,再加上i这一步可以到终点的一种可能性
【3)i+m>n,j+m<=n[A可能一步到终点,B不可能一步到终点]】
(这种情况下,与第2种情况相似)
【4)i+m>n,j+m>n[A、B都有可能一步到终点]】
在这种情况下,因为有反弹,soA、B的位置只可能在[n-m+1,n]中,两人一步到终点的几率都是1/m,
那么,A先到n的可能就是
等比数列求和:
化简得:
【5)最后,还有一点,若i=n-m,当i'=j=n的概率为1】
。
[转自: http://blog.csdn.net/lyd_7_29/article/details/52245309]
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,x,y;
double f[2010][2010];//f[i][j]表示A在第i格,B在第j格时,A获胜的概率
inline double SUM(int x1,int y1,int x2,int y2)
{
return (f[x1][y1]-f[x1][y2]-f[x2][y1]+f[x2][y2]);
}
int main()
{
freopen("dice.in","r",stdin);
freopen("dice.out","w",stdout);
int i,j;
scanf("%d%d%d%d",&n,&m,&x,&y);
for(i=n;i>0;--i)
for(j=n;j>0;--j)
{
f[i][j]=f[i+1][j]+f[i][j+1]-f[i+1][j+1];
if(i==n||j==n) {f[i][j]+=(i==n); continue;}//有一个已到终点
if(i<=n-m&&j<=n-m) {f[i][j]+=SUM(i+1,j+1,i+m+1,j+m+1)/m/m; continue; }//A、B都不能一步到终点
if(i<=n-m&&j>n-m) {f[i][j]+=((m-1)*SUM(i+1,j,i+m+1,j+1)+(i+m==n))/m/m; continue;}//A不能一步到终点,B可能一步到终点
if(i>n-m&&j<=n-m) {f[i][j]+=((m-1)*SUM(i,j+1,i+1,j+m+1)+m)/m/m; continue; }//A可能一步到终点,B不能一步到终点
if(i>n-m&&j>n-m) {f[i][j]+=1.0*m/(2*m-1); continue;}//A、B都可能一步到终点
}
printf("%.6lf\n",SUM(x,y,x+1,y+1));
return 0;
}