【bzoj 3212】【POJ 3468】A Simple Problem with Integers（线段树）

3212: Pku3468 A Simple Problem with Integers

Time Limit: 1 Sec  Memory Limit: 128 MB
Submit: 1568  Solved: 677
[Submit][Status][Discuss]

Description

You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval. 

Input

The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000. 
The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000. 
Each of the next Q lines represents an operation. 
"C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000. 
"Q a b" means querying the sum of Aa, Aa+1, ... , Ab. 

Output

You need to answer all Q commands in order. One answer in a line. 

Sample Input

10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

Sample Output

4
55
9
15

HINT

The sums may exceed the range of 32-bit integers. 

Source

[Submit][Status][Discuss]

【题解】【线段树裸题】

[我假装不懂线段树的样子。。。]

【[概述] 线段树，也叫区间树，是一个完全二叉树，它在各个节点保存一条线段（即“子数组”），因而常用于解决数列维护问题，它基本能保证每个操作的复杂度为O(lgN)。】

【[线段树基本操作] 线段树的基本操作主要包括构造线段树，区间查询和区间修改。】

【如图，即是一棵线段树，每个节点维护的是一个区间的信息（如：最大值、区间和等）】

【定义（范围一般是给定序列的4倍）】

【线段树基本操作之建树：】

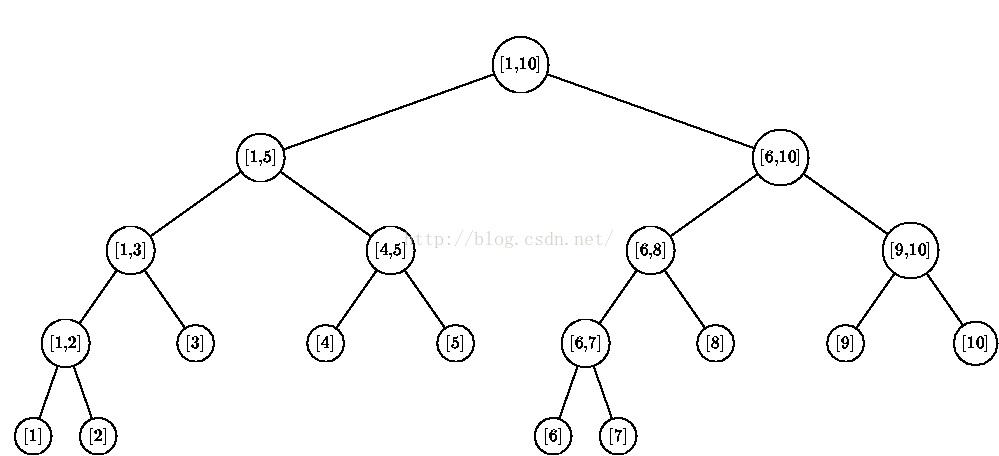
void build(int now,int l,int r)
{
	if(l==r) { sum[now]=(ll)a[l];return; }
	int mid=(l+r)>>1;
	build((now<<1),l,mid);
	build((now<<1)|1,mid+1,r);
	updata(now); 
} 

【线段树基本操作之区间修改（单点修改也可以用这个写，把区间的左右边界定为同一个值即可）：】

void change(int now,int l,int r,int al,int ar,ll val)
{
	if(al<=l&&r<=ar)
	 {
	 	sum[now]+=(ll)(r-l+1)*val;
	 	delta[now]+=(ll)val;
	 	return;
	 }
	int mid=(l+r)>>1;
	pushdown(now,l,mid,r);
	if(al<=mid) change((now<<1),l,mid,al,ar,val);
	if(ar>mid) change((now<<1)|1,mid+1,r,al,ar,val);
	updata(now);
}

【线段树基本操作之区间查询（单点查询也可以用这个写，把区间的左右边界定为同一个值即可）】

ll ask(int now,int l,int r,int al,int ar)
{
	if(al<=l&&r<=ar) return sum[now];
	int mid=(l+r)>>1; ll ans=0;
	pushdown(now,l,mid,r);
	if(al<=mid) ans+=ask((now<<1),l,mid,al,ar);
	if(ar>mid) ans+=ask((now<<1)|1,mid+1,r,al,ar);
	return ans; 
}

【线段树基本操作之标记下传（这是区间求和的）】

inline void pushdown(int now,int l,int mid,int r)
{
	if(delta[now])
	 {
	 	sum[now<<1]+=(ll)(mid-l+1)*delta[now]; sum[now<<1|1]+=(ll)(r-mid)*delta[now];
	 	delta[now<<1]+=delta[now]; delta[now<<1|1]+=delta[now];
	 	delta[now]=0;
	 }
	return;
}

【线段树基本操作之向根更新（这是区间求和的）】

inline void updata(int now)
{
	sum[now]=sum[now<<1]+sum[now<<1|1];
}

——————————————————————————————————————————————

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
ll sum[500010],delta[500010];
int n,q,a[100010];
inline void updata(int now)
{
	sum[now]=sum[now<<1]+sum[now<<1|1];
}
inline void pushdown(int now,int l,int mid,int r)
{
	if(delta[now])
	 {
	 	sum[now<<1]+=(ll)(mid-l+1)*delta[now]; sum[now<<1|1]+=(ll)(r-mid)*delta[now];
	 	delta[now<<1]+=delta[now]; delta[now<<1|1]+=delta[now];
	 	delta[now]=0;
	 }
	return;
}
void build(int now,int l,int r)
{
	if(l==r) { sum[now]=(ll)a[l];return; }
	int mid=(l+r)>>1;
	build((now<<1),l,mid);
	build((now<<1)|1,mid+1,r);
	updata(now); 
}
void change(int now,int l,int r,int al,int ar,ll val)
{
	if(al<=l&&r<=ar)
	 {
	 	sum[now]+=(ll)(r-l+1)*val;
	 	delta[now]+=(ll)val;
	 	return;
	 }
	int mid=(l+r)>>1;
	pushdown(now,l,mid,r);
	if(al<=mid) change((now<<1),l,mid,al,ar,val);
	if(ar>mid) change((now<<1)|1,mid+1,r,al,ar,val);
	updata(now);
}
ll ask(int now,int l,int r,int al,int ar)
{
	if(al<=l&&r<=ar) return sum[now];
	int mid=(l+r)>>1; ll ans=0;
	pushdown(now,l,mid,r);
	if(al<=mid) ans+=ask((now<<1),l,mid,al,ar);
	if(ar>mid) ans+=ask((now<<1)|1,mid+1,r,al,ar);
	return ans; 
}
int main()
{
	freopen("int.txt","r",stdin);
	int i,j;
	scanf("%d%d",&n,&q);
	for(i=1;i<=n;++i) scanf("%d",&a[i]);
	build(1,1,n);
	for(i=1;i<=q;++i)
	 {
	 	char c[10];
	 	scanf("%s",c);
	 	if(c[0]=='Q')
	 	 {
	 	 	int x,y;
	 	 	scanf("%d%d",&x,&y);
	 	 	printf("%lld\n",ask(1,1,n,x,y));
		  }
		if(c[0]=='C')
		 {
		 	int x,y; ll z;
		 	scanf("%d%d%lld",&x,&y,&z);
		 	change(1,1,n,x,y,z);
		 }
	 }
	return 0;
}