【POJ 1112】Team Them Up!（补图+dp(背包)）

Team Them Up!

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 7623		Accepted: 2047		Special Judge

Description

Your task is to divide a number of persons into two teams, in such a way, that: 

everyone belongs to one of the teams; 

every team has at least one member; 

every person in the team knows every other person in his team; 

teams are as close in their sizes as possible. 

This task may have many solutions. You are to find and output any solution, or to report that the solution does not exist.

Input

For simplicity, all persons are assigned a unique integer identifier from 1 to N. 

The first line in the input file contains a single integer number N (2 <= N <= 100) - the total number of persons to divide into teams, followed by N lines - one line per person in ascending order of their identifiers. Each line contains the list of distinct numbers Aij (1 <= Aij <= N, Aij != i) separated by spaces. The list represents identifiers of persons that ith person knows. The list is terminated by 0.

Output

If the solution to the problem does not exist, then write a single message "No solution" (without quotes) to the output file. Otherwise write a solution on two lines. On the first line of the output file write the number of persons in the first team, followed by the identifiers of persons in the first team, placing one space before each identifier. On the second line describe the second team in the same way. You may write teams and identifiers of persons in a team in any order.

Sample Input

5
2 3 5 0
1 4 5 3 0
1 2 5 0
1 2 3 0
4 3 2 1 0

Sample Output

3 1 3 5
2 2 4

Source

Northeastern Europe 2001

[Submit]   [Go Back]   [Status]   [Discuss]

Home Page   Go Back  To top

[题意][把所有的点分为两部分，要求：1）每个人都属于一个区域 2）每个组都至少包括一个点  3）每个区域中的所有点必须互相连通 4）两个组的人数应该尽量相近]

【题解】【补图+dp】

【先在读入的同时建出图，由于题目给的是有向图，那么a和b联通不代表b和a联通，这样一来，在考虑两个点能否在同一组时就比较麻烦了】

【真理：正难则反易！】【把原来的有向图转变为它的补图：没边的连边，如果只有一条有向边，也连边。注：补图是个无向图。 那么，在补图中有边的两个点就不能放在一个组中】

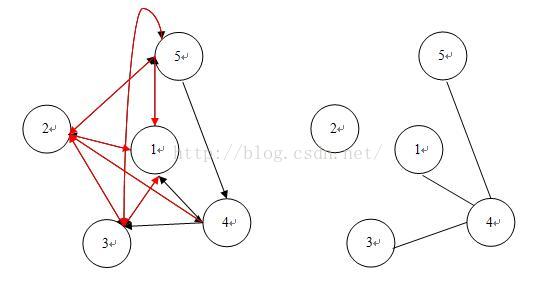
【类似于黑白染色，给有边相连的点染成不同的颜色。然后判断这个图是否能满足分成两个区域，即相同颜色的点之间没有边，如果不满足，直接输出"No solution" 】

【在染色时，存储当前情况下，白点和黑点各有多少。】

【dp】

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int a[20010],nxt[20010],p[110],tot;
int f[110][110],g[110][110],num[110][2][110];
int n,cnt,tt,point[110];
int mp[110][110],fmp[110][110],vis[110];
inline int abss(int x)
{
	if(x>=0) return x;
	return -x;
}
inline void add(int x,int y)
{
	tot++; a[tot]=y; nxt[tot]=p[x]; p[x]=tot;
	tot++; a[tot]=x; nxt[tot]=p[y]; p[y]=tot;
}
void dfs(int x,int opt)
{
	vis[x]=1; num[cnt][opt][0]++;
	int t=num[cnt][opt][0]; num[cnt][opt][t]=x;
	for(int i=p[x];i!=-1;i=nxt[i])
	 if(!vis[a[i]]) dfs(a[i],opt^1);
}
inline void rebuild()
{
	for(int i=1;i<n;++i)
	 for(int j=i+1;j<=n;++j)
	  if(!mp[i][j]||!mp[j][i])
	   add(i,j),fmp[i][j]=fmp[j][i]=1;
	for(int i=1;i<=n;++i)
	 if(!vis[i]) cnt++,dfs(i,0);
}
inline bool recheck()
{
	for(int i=1;i<=cnt;++i)
	 for(int l=0;l<2;++l)
	  {
	  	int t=num[i][l][0];
	  	for(int j=1;j<t;++j)
	  	 for(int k=j+1;k<=t;++k)
	  	  {
	  	  	int x=num[i][l][j],y=num[i][l][k];
	  	  	if(fmp[x][y]||fmp[y][x]) {printf("No solution\n"); return 1;}
			}
	  }
	return 0;
}
inline void dp()
{
	int x=num[1][0][0],y=num[1][1][0];
	f[1][x]=1; g[1][x]=0;
	f[1][y]=1; g[1][y]=1;
	for(int i=0;i<=n;++i)
	 for(int j=2;j<=cnt;++j)
	   {
	   	    if(f[j][i]) continue;
	   	    int x=num[j][0][0],y=num[j][1][0];
	   	    if(i-x>=0&&f[j-1][i-x]) f[j][i]=1,g[j][i]=0;
	   	    if(i-y>=0&&f[j-1][i-y]) f[j][i]=1,g[j][i]=1;
	   }
}
inline void find()
{
	int pre=n,ans=n;
    for(int i=n;i>0;--i)
     if(f[cnt][i]) 
      {
      	int t=abss(n-i*2);
      	if(ans>t) ans=t,pre=i;
	  }
	for(int i=cnt;i>0;--i)
	 {
	 	int t=g[i][pre],x=num[i][0][0],y=num[i][1][0];
	 	for(int j=1;j<=num[i][t][0];++j) point[++tt]=num[i][t][j];
	 	if(t) pre-=y;
	 	 else pre-=x;
	 }
}
int main()
{
	int i;
	memset(nxt,-1,sizeof(nxt));
	memset(p,-1,sizeof(p));
	scanf("%d",&n);
	for(i=1;i<=n;++i)
	 {
	 	int x;
	 	while(scanf("%d",&x)==1&&x) mp[i][x]=1;
	 }
	rebuild();
	if(recheck()) return 0;
	dp();
	find();
	memset(vis,0,sizeof(vis));
	printf("%d ",tt);
	for(i=1;i<=tt;++i) vis[point[i]]=1,printf("%d ",point[i]);
	printf("\n%d ",n-tt);
	for(i=1;i<=n;++i)
	 if(!vis[i]) printf("%d ",i);
	return 0;
}