【codevs 1922】骑士共存问题（最大流DINIC）

1922 骑士共存问题

   时间限制: 2 s  空间限制: 256000 KB   题目等级 : 大师 Master

题目描述 Description
  在一个n*n个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入。 对于给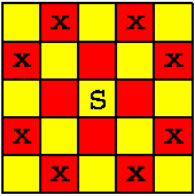定的n*n个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击。
输入描述 Input Description
  第一行有2 个正整数n 和m (1<=n<=200, 0<=m<n^2)，分别表示棋盘的大小和障碍数。接下来的m 行给出障碍的位置。每行2 个正整数，表示障碍的方格坐标。

输出描述 Output Description    

  将计算出的共存骑士数输出

样例输入 Sample Input
  3 2
  1 1
  3 3
样例输出 Sample Output

   5

【题解】【网络流最大流】

【黑白染色，只是骑士跳“日”，所以白点和黑点连边时，要按照其实一次能跳到的位置来连，还有就是有不能放骑士的地方，要特判不能放。我先将不能放的点打上标记，然后枚举整个矩阵并将能放骑士的点依次编号，随后再建图】 

#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define lng 10000000
using namespace std;
int d[210][210];
int a[400010],next[400010],p[400010],remain[400010],tot;
int dis[400010],cur[400010];
int n,m,n1,cnt,ans;

inline void add(int x,int y,int flow)
{
	tot++; a[tot]=y; next[tot]=p[x]; p[x]=tot; remain[tot]=flow;
	tot++; a[tot]=x; next[tot]=p[y]; p[y]=tot; remain[tot]=0;
	return;
}
inline void check(int a1,int x,int y)
{
	if (d[x][y]>0&&x>0&&y>0&&x<=n&&y<=n) add(a1,d[x][y],lng);
	return; 
}

inline bool bfs()
{
	queue<int>que;
	memset(dis,-1,sizeof(dis));
	for (int i=0;i<=n1;++i)
	 cur[i]=p[i];
	que.push(0); dis[0]=0;
	while (!que.empty())
	 {
	 	int u,v;
	 	u=que.front(); que.pop();
	 	v=p[u];
	 	while (v!=-1)
	 	 {
	 	 	if (remain[v]&&dis[a[v]]<0)
	 	 	 {
	 	 	 	dis[a[v]]=dis[u]+1;
	 	 	 	que.push(a[v]);
	 	 	 }
	 	 	v=next[v];
	 	 }
	 }
	if (dis[n1]<0) return false;
	 else return true;
}
inline int dfs(int now,int flow)
{
	if (now==n1||flow==0) return flow;
	int u=cur[now],s;
	while (u!=-1)
	 {
	 	cur[now]=u;
	 	if (dis[a[u]]>0&&dis[a[u]]==dis[now]+1&&(s=dfs(a[u],min(flow,remain[u]))))
	 	 {
	 	 	remain[u]-=s; remain[u^1]+=s;
	 	 	return s;
	 	 }
	 	u=next[u];
	 }
	return 0;
}

int main()
{
	int i,j;
	memset(p,-1,sizeof(p));
	memset(next,-1,sizeof(next));
	scanf("%d%d",&n,&m);
        tot=-1;
	for (i=1;i<=m;++i)
	 {
	 	int x,y;
	 	scanf("%d%d",&x,&y);
	 	d[x][y]=-1;
	 }
	for (i=1;i<=n;++i)
	 for (j=1;j<=n;++j)
	   if (!d[i][j])
	    d[i][j]=++n1;
	n1++;
    for (i=1;i<=n;++i)
     for (j=1;j<=n;++j)
      if (d[i][j]>0)
       {
       	if (i%2==j%2)
       	 {
       	 	add(0,d[i][j],1);
			check(d[i][j],i-1,j-2); check(d[i][j],i-1,j+2);
			check(d[i][j],i-2,j-1); check(d[i][j],i-2,j+1);
			check(d[i][j],i+1,j-2); check(d[i][j],i+1,j+2);
			check(d[i][j],i+2,j-1); check(d[i][j],i+2,j+1);
       	 }
       	else add(d[i][j],n1,1);
       }
   while (bfs())
    while (cnt=dfs(0,0x7fffffff))
     ans+=cnt;
   ans=n1-ans;
   printf("%d",ans-1);
   return 0;
}