【NOIP 模拟题】[T3] 光（莫比乌斯反演）

光

【问题描述】
天猫有一个长方形盒子，长宽分别为 A，B。这个长方形盒子的内壁全部是镜面。天猫在这个盒子的左下方放了一个激光灯。这个灯可以照向盒子内的任意角度。现在天猫想要打开这个激光灯，但是他想让光线按照如下规则照射：
1.这束光必须恰好打到盒子边缘反射 D 次，并且不能碰到任意一个角落（除了出发点以及结束点）。
2.这束光必须到达盒子右上角，并且结束反射。
天猫想要知道，所有合法的光线路线的长度平方和是多少。作为一个资深 OIer，你应该知道输出要对 10^9+7 取模。
【输入文件】
一行三个数，表示 A，B，D。
【输出文件】
一行表示路线长度的平方和。
【样例输入】
[sample 1]
3 4 0
[sample 2]
3 3 2
【样例输出】
[sample 1]
25
[sample 2]
180
【数据范围】
对于 20%的数据，D<=2
对于 40%的数据，D<=10
对于 70%的数据，D<=10^6
对于 100%的数据，D<=10^9, A,B<=10^6

【题解】【莫比乌斯反演】

【由于通过盒子的四壁反射是镜面反射，那么由物理只是可知反射的路线相当于关于镜面对称的】

如图：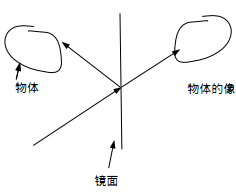

那么就相当于又伸展出一个盒子

【那么，就相当于给定一个D*D的盒子，然后在里面寻找一个整数点（x，y）的个数。由于当有横向有x个矩形时是打到左右边界x-1次，当纵向有y个矩阵时是打到上下边界y-1次，那么x、y需要满足的条件就是x+y-2=D】

这样，我们要求的实际上就是

∑x=0D+2[(x,D+2−x)=1]x2∗A2+(D+2−x)2∗B2

容易知道，gcd(x,y)=1 => gcd(x,x+y)=1,那么实际上，A2和B2的系数可以互换，所以原式又可以化成：

A2+B2∑x=0D+2[(x,D+2)=1]x2

那么，问题就转化为求：

∑i=1n[(i,n)=1]i2

反演得到：

∑i=nni2∑d|nμ(d)

设i=id,则

∑d|nμ(d)∑⌊nd⌋i2=∑d|nμ(d)d2⌊nd⌋+(2∗⌊nd⌋+1)+(⌊nd⌋+1)6

【所以我们只需求出d和miu[d]即可。】

【μ：若x为质数或有奇数个质因子，那么μ（x）=-1；若x有偶数个不同的质因子，那么μ（x）=1；若x有次数不为一的质因子，那么μ（x）=0，即此时没有贡献。所以，只需考虑μ（x）等于±1的情况即可。用类似状压dp的方法求出当前状态下的μ值，以及这个状态质因子次数都为1时的μ值。】

[注：代码里求的poww(6,mod-2)，实际上是把(mod p)意义下的除6，转变为乘6的逆元]**

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
#define mod 1000000007
using namespace std;
ll d[1<<10],miu[1<<10],ans;
int a,b,k,cnt;
ll poww(int x,ll p)
{
    if(p==0) return 1;
    if(p==1) return x%mod;
    if(p&1)
     {
        ll a=poww(x,p/2)%mod;
        a*=a; a%=mod;
        a*=x;
        return a%mod;
      } 
     else
      {
        ll a=poww(x,p/2)%mod;
        a*=a; a%mod;
        return a;
      }
}
int main()
{
    freopen("light.in","r",stdin);
    freopen("light.out","w",stdout);
    scanf("%d%d%d",&a,&b,&k); k+=2;
    if(k&1) {printf("0\n"); return 0;}
    if(!k) {printf("%d\n",(a*a+b*b)%mod); return 0;}
    ll md=poww(6,mod-2);
    int x=k;
    for(int i=2;i*i<=k;++i)
     if(!(x%i))
      {
        d[1<<cnt]=i; miu[1<<cnt]=-1; cnt++; 
        while(!(x%i)) x/=i;
      }
    if(x>1) d[1<<cnt]=x,miu[1<<cnt]=-1,cnt++;
    for(int i=0;i<(1<<cnt);++i)
     {
        if(i) miu[i]=-miu[i^i&(-i)],d[i]=d[i^i&(-i)]*d[i&(-i)];
         else d[i]=miu[i]=1;
        int x=k/d[i];
        ans=(ans+(miu[i]%mod*d[i]%mod*d[i]%mod)%mod*x%mod*(x+1)%mod*(2*x+1)%mod*md%mod)%mod;
     }
    ans=(ans*a%mod*a%mod+ans*b%mod*b%mod)%mod;
    ans=(ans+mod)%mod;
    printf("%I64d\n",ans);
    return 0;
}