二分查找算法
二分查找算法思想
1、数组要求是有序的
2、定义左右边界索引l、r，中间索引m=(l+r)/2
3、判断arr[m]与待查找值target的大小，不断减少右边界索引r或者增加左边界索引l
基础版二分查找
（1）如果target<arr[m]，则证明待查找值在中间索引左侧，减少右索引r=m-1，继续下一轮查找
（2）如果如果target>arr[m]，则证明待查找值在中间索引右侧，增加左索引l=m+1，继续下一轮查找
（3）如果如果target=arr[m]，则证明找到待查找值，返回对应索引
（4）循环结束了l>r还没找到，即没有待查找值，返回-1
基础版代码：
public static int binarySearch(int [] arr,int target){
int l = 0, r=arr.length-1;
while (l<=r){
int m = (l+r)>>>1;
if(target<arr[m]){
r=m-1;
}else if(arr[m]<target){
l=m+1;
}else {
return m;
}
}
return -1;
}基础版二分查找算法性能分析：
1、最好情况：O(1)，第一次循环的值就是待查找值
2、最坏情况：O(log(n))
平衡版二分查找
在上述基础版二分查找算法中，如果待查找元素在最左侧L次循环的位置，则需要执行L次，即每次只需要执行if(target<arr[m])分支，而待查找元素在最右侧L次的位置时候，则需要执行2L次，即每次既需要执行if(target<arr[m])分支，又需要执行if(arr[m]<target)。元素在左侧和右侧的执行效率不一样，在左侧时查找速率更快，在右侧时查找速率要慢点，平衡版二分查找可以让左侧右侧的效率都保持一样，下面给出左右查找效率一样平衡版二分查找的实现思路：
1、左闭右开的区间，左边界索引l可能是查找目标，而右边界索引r不可能是查找目标
2、不在循环内找出，等循环只剩下l时，退出循环，在循环外比较arr[l]与target
public static int binarySearch2(int [] arr,int target){
int l = 0, r=arr.length;
while (1 <r-l ){
int m = (l+r)>>>1;
if(target<arr[m]){
r=m;
}else {
l=m;
}
}
if(arr[l]==target){
return l;
}else {
return -1;
}
}平衡版二分查找中，无论待查找元素在最左侧L次还是在最右侧L次的位置，都是只需要执行if(target<arr[m])分支，执行次数都是L次，时间复杂度最好最坏情况都是O(log(n))，没有最好情况O(1)，因为最好最坏情况都是执行完循环在循环外边判断是否找到值，可以认为是不快不慢算法，待查找元素在靠左侧还是在靠右侧查找效率一样，而上面的基础版二分查找待查找元素在靠左侧的查找效率要高一些
最左、右侧匹配的二分查找（LeftRightMost）
场景提出：上述的二分查找算法中，返回的元素不一定就是最左匹配的元素，下面给出最左侧匹配算法的思路：
1、定义一个候选者变量
2、如果找到待查找元素，则将m赋值到候选者，记录候选者位置
3、继续缩小查找范围，重复更新候选者位置
最左侧匹配的二分查找（LeftMost）
public static int binarySearchLeftMost(int [] arr,int target){
int l = 0, r=arr.length-1;
int candidate=-1;
while (l<=r){
int m = (l+r)>>>1;
if(target<arr[m]){
r=m-1;
}else if(arr[m]<target){
l=m+1;
}else {
//找到元素了，不直接返回m，而是记录候选者位置，继续缩小查找范围
candidate = m;
r = m-1;
}
}
return candidate;
}
最左侧匹配的二分查找（LeftMost）-返回特定值
在上述算法，没有找到目标值时，返回的-1实际没什么意义，我们有时候希望在没找到元素时，可以返回≥target的最左侧索引
public static int binarySearchLeftMost2(int [] arr,int target){
int l = 0, r=arr.length-1;
while (l<=r){
int m = (l+r)>>>1;
if(target<=arr[m]){
//无论target是否找到还是没找到，都继续缩小范围
r=m-1;
} else {
l=m+1;
}
}
//返回的l是≥target的最左侧索引
return l;
}如测试用例1：
System.out.println(binarySearchLeftMost2(new int[]{1,2,5,5,5,8,8,8,10,22},7));该结果会返回5，就是返回比待查找值'7'大的最左侧的那个值'8'的索引位置
测试用例2：
System.out.println(binarySearchLeftMost2(new int[]{1,2,5,5,5,8,8,8,10,22},5));返回的是2，即找到待查找值'5'最左侧的的索引位置
最右侧匹配的二分查找（RightMost）
public static int binarySearchRightMost(int [] arr,int target){
int l = 0, r=arr.length-1;
int candidate=-1;
while (l<=r){
int m = (l+r)>>>1;
if(target<arr[m]){
r=m-1;
}else if(arr[m]<target){
l=m+1;
}else {
//找到元素了，不直接返回m，而是记录候选者位置，继续缩小查找范围
candidate = m;
l = m+1;
}
}
return candidate;
}
最右侧匹配的二分查找（RightMost）-返回特定位置
public static int binarySearchRightMost2(int [] arr,int target){
int l = 0, r=arr.length-1;
while (l<=r){
int m = (l+r)>>>1;
if(target<arr[m]){
r=m-1;
}else {
//无论target是否找到还是没找到，都继续缩小范围
l=m+1;
}
}
//返回的l-1是≤target的最右侧索引
return l-1;
}如测试用例1：
System.out.println(binarySearchRightMost2(new int[]{1,2,5,5,5,8,10,22},7));该结果返回的是：4，返回的是比待查找值'7'小的最靠右的那个元素'5'的索引位置
测试用例2：
System.out.println(binarySearchRightMost2(new int[]{1,2,5,5,5,8,8,8,10,22},8));该结果返回的是：7，即找到待查找值'8'最右侧的的索引位置
最左、右侧匹配查找的应用
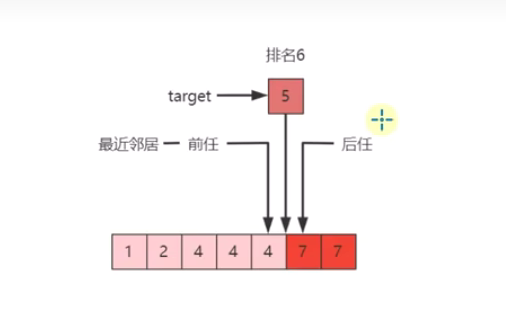
名词解析：前任：<targert的最靠右侧元素（rightMost），后任：>target的最靠左侧元素（leftMost），最近邻居：前任后任看哪个位置举例target更近（target-rightMost索引的值与leftMost索引的值-target作比较取更小的）
力扣704题：
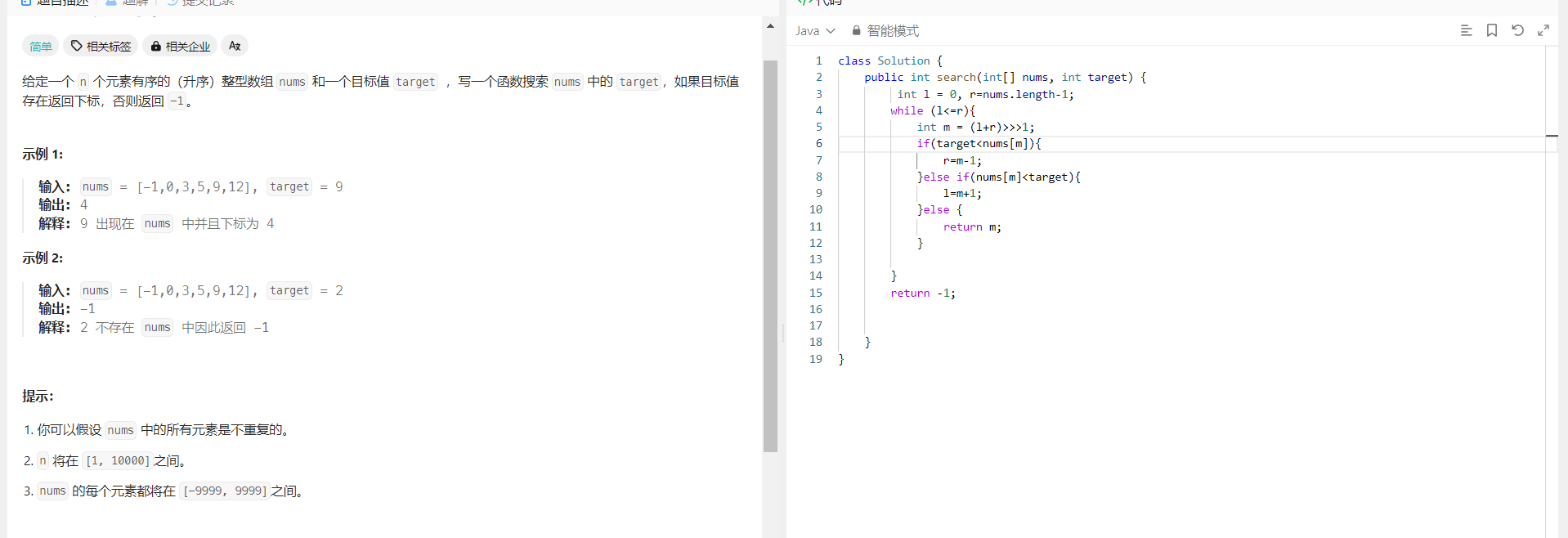
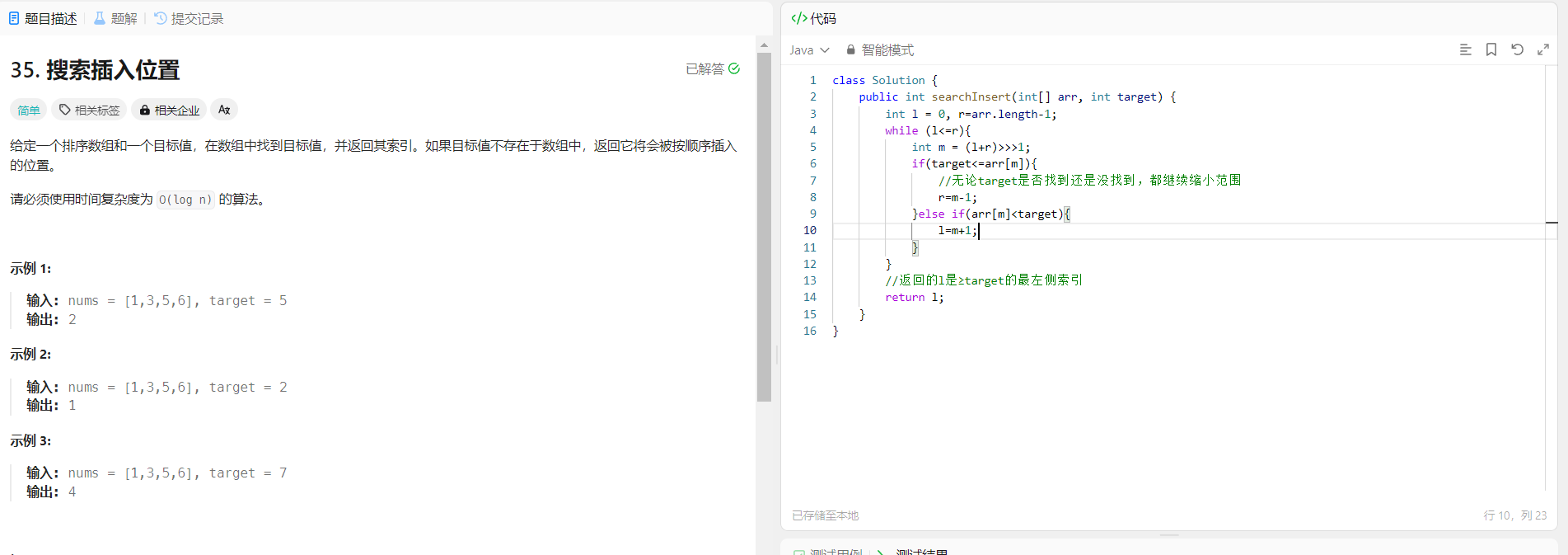
力扣35题：使用leftMost
