北京化工大学程序设计周赛 Contest2173 - 2021-2022-1 ACM集训队每周程序设计竞赛（4） A.异或&加法 (位运算,dp)

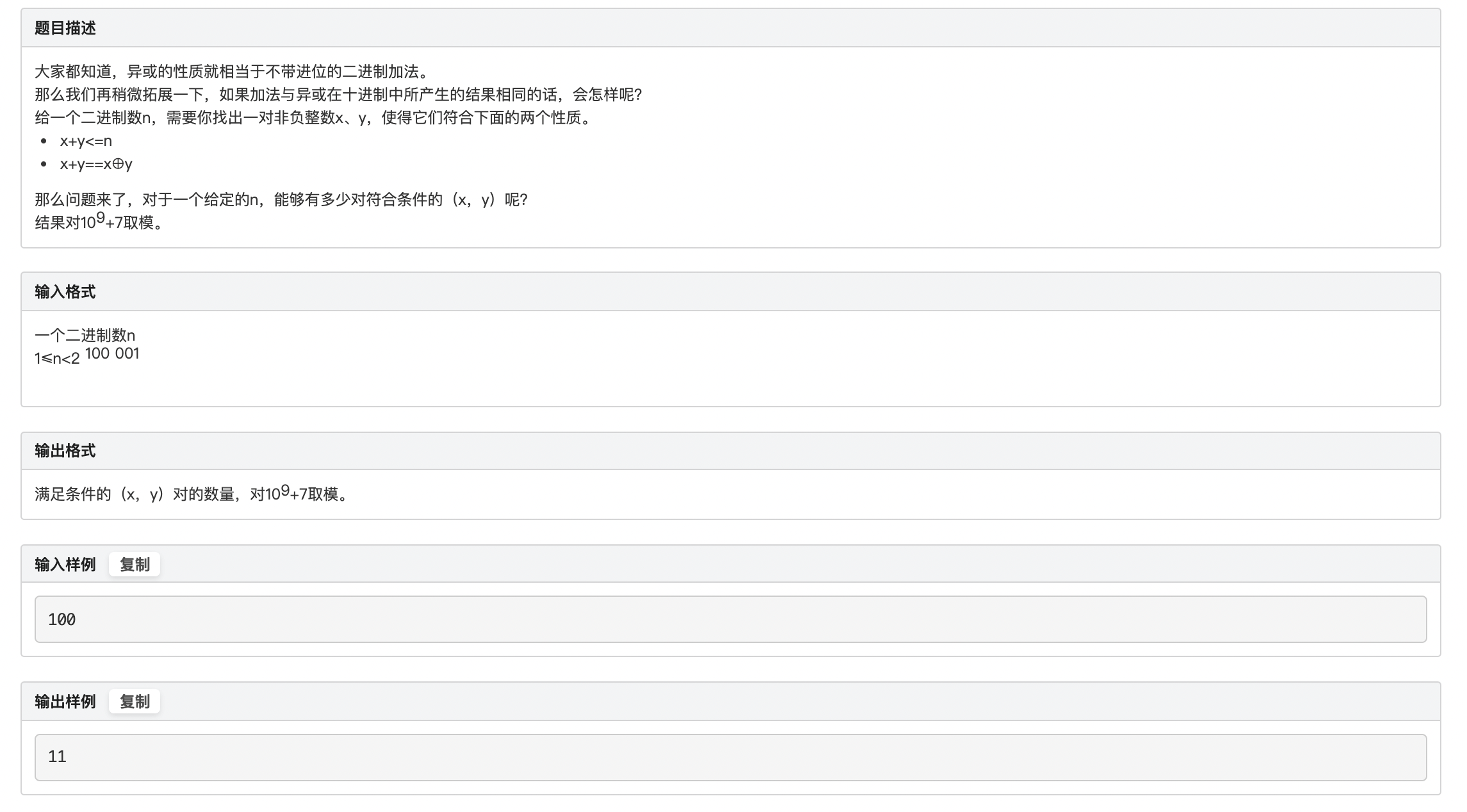
• 题意：给你一个二进制数，求有多少对\((x,y)\)满足图中的两个条件。

• 题解：对于\(x+y=x\oplus y\)，我们知道异或是不进位的，那么就要保证\(x\)和\(y\)的任意一位不同时为\(1\)，先看\(x+y=n\)的情况，这很容易就能算出来，关键是\(x+y\le n\)怎么搞，我们假设\(dp[0][i]\)表示\(x+y\)的前\(i\)位都与\(n\)的前\(i\)位相同，\(dp[1][i]\)表示\(x+y\)的前\(i\)位至少有一个位置，小于\(n\)对应的位置，那么在这之后，我们随便怎么赋值(除了\((1,1)\)，都能满足图中的两个条件。那么：

  假设\(n\)的第\(i\)位是\(0\),有:\(dp[0][i]=dp[0][i-1]\)，因为只能选\((0,0\))。\(dp[1][i]=dp[1][i-1]*3\)，因为必然合法，\((0,0),(0,1),(1,0)\)随便选

  假设\(n\)的第\(i\)位是\(1\),有:\(dp[0][i]=dp[0][i-1]*2\)，因为可以选\((0,1),(1,0)\)。\(dp[1][i]=dp[1][i-1]*3+dp[0][i-1]\)，这里加上\(dp[0][i-1]\)是因为可以选\((0,0)\)来表示直到当前这个位置才满足小于的情况。

  最后记得初始化，\(dp[0][0]=1\).

• 代码：

  #include <bits/stdc++.h>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  #define rep(a,b,c) for(int a=b;a<=c;++a)
  #define per(a,b,c) for(int a=b;a>=c;--a)
  const int N = 3e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
  ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
  
  string s;
  ll dp[2][N];
  
  int main() {
  	cin>>s;
  	int n=(int)s.size();
  	s=" "+s;
  	dp[0][0]=1;
  	for(int i=1;i<=n;++i){
  		if(s[i]=='0'){
  			dp[0][i]=dp[0][i-1];
  			dp[1][i]=dp[1][i-1]*3%mod;
  		}
  		else{
  			dp[0][i]=dp[0][i-1]*2%mod;
  			dp[1][i]=(dp[1][i-1]*3%mod+dp[0][i-1])%mod;
  		}
  	}
  	printf("%lld\n",(dp[0][n]+dp[1][n])%mod);
  	return 0;
  }