【洛谷】P4310 绝世好题 (二进制，dp)

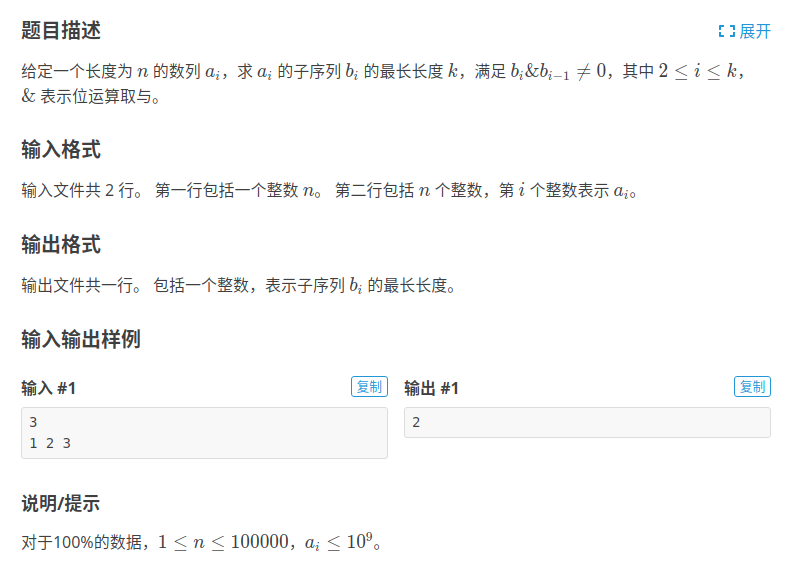
• 题意：长度为\(n\)的序列\(a\)，求其子序列\(b\)的最长长度，使得\(b[i]\)&\(b[i-1]\neq 0\ \ \ 2\le i\le k\).

• 题解：\(dp[j]\)表示二进制的\(j\)位的最大贡献，对于每个\(a[i]\)，遍历它的二进制每一位\(1\)，那么当前状态就可以从这些\(1\)的位置转移过来，先找出当前状态的最大值\(mx=max(mx,dp[j]+1)\)，然后再更新\(a[i]\)的二进制上的每一位\(1\).

• 代码：

  #include <bits/stdc++.h>
  #define ll long long
  #define fi first
  #define se second
  #define me memset
  #define rep(a,b,c) for(int a=b;a<=c;++a)
  #define per(a,b,c) for(int a=b;a>=c;--a)
  const int N= 1e6+10;
  const int mod=1e9+7;
  const int INF= 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
  ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
  
  int n;
  int a[N];
  int dp[N];
  
  int main(){
      scanf("%d",&n);
      for(int i=1;i<=n;++i){
          scanf("%d",&a[i]);
      }
      int ans=0;
      for(int i=1;i<=n;++i){
          int mx=0;
          for(int j=0;j<32;++j){
              if((1<<j)&a[i]) mx=max(mx,dp[j]+1);
          } 
          for(int j=0;j<32;++j){
              if((1<<j)&a[i]) dp[j]=max(dp[j],mx);
          }
          ans=max(ans,mx);
      }
      printf("%d\n",ans);
      return 0;
  }