AtCoder Beginner Contest 221 E - LEQ (计数,线段树)
-
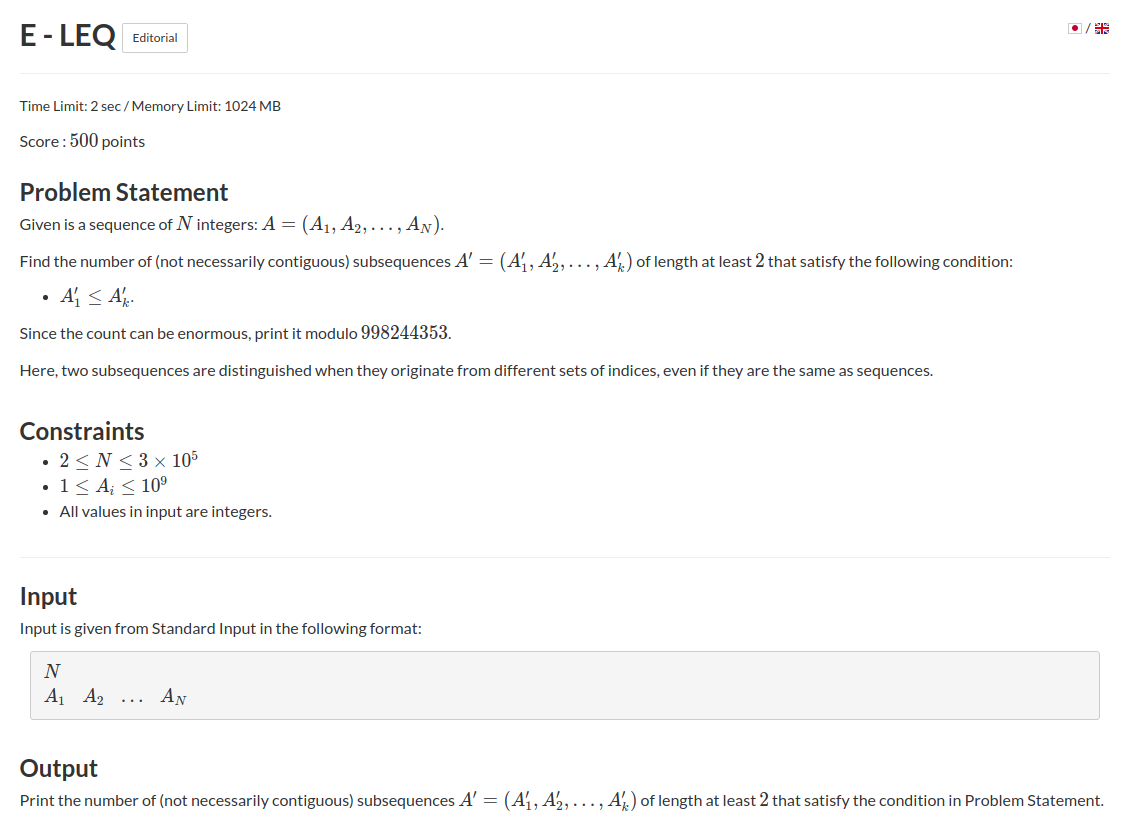
题意:给你一个长度为\(n\)的序列,问你有多少子序列满足第一个元素不大于最后一个元素。
-
题解:假设子序列的尾元素在原序列的位置为\(j\),如果\(i\ (i<j)\)位置满足\(A[i]\le A[j]\),那么,\([i,j]\)的合法子序列个数为\(2^{j-i-1}\),因为一定选\(i\)和\(j\),中间的部分有\(j-i-1\)个数,子集个数就为\(2^{j-i-1}\),那么我们遍历每个位置,当成\(j\),找\([1,j-1]\)有多少\(i\)满足\(A[i]\le A[j]\),每个\(i\)的贡献为\(\frac{2^{j-1}}{2^i}\),每次找区间元素符合条件的个数,单点修改,用权值线段树即可。
-
代码:
#include <bits/stdc++.h> #define ll long long #define fi first #define se second #define pb push_back #define me memset #define rep(a,b,c) for(int a=b;a<=c;++a) #define per(a,b,c) for(int a=b;a>=c;--a) const int N = 1e6 + 10; const int mod = 998244353; const int INF = 0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; typedef pair<ll,ll> PLL; ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;} ll lcm(ll a,ll b) {return a/gcd(a,b)*b;} int n; int a[N]; vector<int> all; struct Node{ int l,r; int cnt; }tr[N<<4]; int get(int x){ return lower_bound(all.begin(),all.end(),x)-all.begin(); } ll fpow(ll a,ll k){ ll res=1; while(k){ if(k&1) res=res*a%mod; k>>=1; a=a*a%mod; } return res; } void push_up(int u){ tr[u].cnt=(tr[u<<1].cnt+tr[u<<1|1].cnt)%mod; } void build(int u,int l,int r){ if(l==r){ tr[u]={l,r,0}; return; } tr[u]={l,r,0}; int mid=(l+r)>>1; build(u<<1,l,mid); build(u<<1|1,mid+1,r); push_up(u); } void update(int u,int x,int val){ if(tr[u].l==tr[u].r){ tr[u].cnt=(tr[u].cnt+val)%mod;; return; } int mid=(tr[u].l+tr[u].r)>>1; if(x<=mid) update(u<<1,x,val); else update(u<<1|1,x,val); push_up(u); } ll query(int u,int L,int R){ if(tr[u].l>=L && tr[u].r<=R){ return tr[u].cnt; } int mid=(tr[u].l+tr[u].r)>>1; ll sum=0; if(L<=mid) sum=(sum+query(u<<1,L,R))%mod; if(R>mid) sum=(sum+query(u<<1|1,L,R))%mod; return sum; } int main() { scanf("%d",&n); for(int i=1;i<=n;++i){ scanf("%d",&a[i]); all.pb(a[i]); } sort(all.begin(),all.end()); all.erase(unique(all.begin(),all.end()),all.end()); build(1,0,(int)all.size()-1); ll ans=0; for(int i=1;i<=n;++i){ ll now=fpow(2,i); ans=(ans+query(1,0,get(a[i]))*fpow(2,i-1)%mod)%mod; update(1,get(a[i]),fpow(now,mod-2)); } printf("%lld\n",ans); return 0; }
𝓐𝓬𝓱𝓲𝓮𝓿𝓮𝓶𝓮𝓷𝓽 𝓹𝓻𝓸𝓿𝓲𝓭𝓮𝓼 𝓽𝓱𝓮 𝓸𝓷𝓵𝔂 𝓻𝓮𝓪𝓵
𝓹𝓵𝓮𝓪𝓼𝓾𝓻𝓮 𝓲𝓷 𝓵𝓲𝓯𝓮

