AtCoder Beginner Contest 220 A~F 题解

AtCoder Beginner Contest 220

A - Find Multiple

水题

B - Base K

水题

C - Long Sequence

• 题意：有长度为\(n\)的序列\(A\)，\(B\)由连续\(10^{100}\)个\(A\)拼接而成，给你一个\(X\)，问你\(B\)的最小的前缀和位置\(k\)，使得\(\sum^{k}_{i=1}B_i>X\).

• 题解：先统计\(A\)的\(sum\)和前缀和，\(cnt\)为\(X|sum\)的块数，\(rest\)为剩下的余数，然后二分找\(rest\)在\(A\)的前缀和第一个大于的位置\(pos\)，\(cnt*n+rest\)即为答案。

• 代码：

  #include <bits/stdc++.h>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  #define rep(a,b,c) for(int a=b;a<=c;++a)
  #define per(a,b,c) for(int a=b;a>=c;--a)
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
  ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
  
  int n;
  ll a[N];
  ll x;
  ll pre[N];
  
  int main() {
      scanf("%d",&n);
      ll sum=0;
      for(int i=1;i<=n;++i){
          scanf("%lld",&a[i]);
          sum+=a[i];
          pre[i]=pre[i-1]+a[i];
      }
      scanf("%lld",&x);
      ll cnt=x/sum;
      ll rest=x%sum;
      int pos=upper_bound(pre+1,pre+1+n,rest)-pre;
      printf("%lld\n",cnt*n+pos);
      return 0;
  }
  
  

D - FG operation

• 题意：有长度为\(n\)的序列\(A\)，每个元素由\([0,9]\)构成，每次有两种操作，一是取出序列的前两个元素\(x\)和\(y\)，pop掉，然后在队头放入\((x+y)\mod 10\).另外一种是放入\((x*y)\mod 10\)，问你最后序列剩一个数的时候\([0,9]\)的方案数。

• 题解：元素范围\([0,9]\)，很明显可以二维dp，设\(dp[i][now]\)表示第\(i\)次操作，操作完后队头元素为\(now\)的方案数，那么我们枚举上一个位置的所有可能情况\([0,9]\)，得到：\(dp[i][now]=dp[i][now]+dp[i-1][j]\).结束！

• 代码：

  #include <bits/stdc++.h>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  #define rep(a,b,c) for(int a=b;a<=c;++a)
  #define per(a,b,c) for(int a=b;a>=c;--a)
  const int N = 1e5 + 10;
  const int mod = 998244353;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
  ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
  
  int n;
  ll a[N];
  ll dp[N][10];
  
  int main() {
      scanf("%d",&n);
      for(int i=1;i<=n;++i){
          scanf("%lld",&a[i]);
      }
      dp[1][a[1]]=1;
      for(int i=2;i<=n;++i){
          for(int j=0;j<10;++j){
              dp[i][(a[i]+j)%10]=(dp[i][(a[i]+j)%10]+dp[i-1][j])%mod;
              dp[i][(a[i]*j)%10]=(dp[i][(a[i]*j)%10]+dp[i-1][j])%mod;
          }
      }
      for(int i=0;i<10;++i){
          printf("%lld\n",dp[n][i]);
      }
      return 0;
  }
  
  

E - Distance on Large Perfect Binary Tree

• 题意：有一颗\(2^n-1\)个结点的完全二叉树，边权为\(1\)，问你有多少点对\((i,j)\)它们的最短路径为\(D\).注意\((i,j)\)和\((j,i)\)不相同。

• 题解：对每个点考虑贡献，那么有两种情况，一种是只在左子树或者右子树上有点对，这个时候路径是一条链，那么满足条件的点就有\(2^{D-1}\)个，因为左子树和右子树等同，所以贡献为\(2^D\)。再来考虑\(D\)被左右子树分摊的情况，这时候左子树和右子树都至少要贡献一个距离，我们假设左或右子树能贡献的最远距离为\(r\ (r\ge 1)\)，那么另外一颗子树能贡献的最小距离\(l=d-r\ (l\ge 1)\)，想象一下一根链子挂在父亲结点左右滑动，那么就有\(r-l+1\)种情况，假设左子树的距离为\(l\)，右子树的距离为\(r\)，那么贡献为\((r-l+1)*2^{l-1}*2^{r-1}=(r-l+1)*2^{D-2}\)。因为是一颗完全二叉树，所以只用每一层的一个结点，然后乘上那一层结点的个数即可\(O(1)\)算每一层的结点的贡献，还要注意判断距离是否合法，即距离是否超过了当前结点到叶子结点的距离。最后对答案*2即可。

• 代码：

  #include <bits/stdc++.h>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  #define rep(a,b,c) for(int a=b;a<=c;++a)
  #define per(a,b,c) for(int a=b;a>=c;--a)
  const int N = 3e6 + 10;
  const int mod = 998244353;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
  ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
  
  int n,d;
  ll pw[N];
  
  int main() {
      scanf("%d %d",&n,&d);
      pw[0]=1;    
      for(int i=1;i<=2*n;++i){
          pw[i]=(pw[i-1]*1ll*2)%mod;
      }
      ll ans=0;
      for(int i=1;i<=n;++i){
          int mx=n-i;
          if(d<=mx){  
              ans=(ans+pw[d]*pw[i-1]%mod)%mod;
          }
          int r=min(mx,d-1);  //左右子树分摊(即左右子树至少存在一个点)，r表示左或右子树能到达的最远的度
          int l=d-r;
          if(l>r) continue;
          ans=(ans+(r-l+1)*pw[d-2]%mod*pw[i-1]%mod)%mod;
      }
      printf("%lld\n",ans*2%mod);
      return 0;
  }
  
  

F - Distance Sums 2

• 题意：一颗\(n\)个结点的树，边权为\(1\),对于每个点\(i\)，计算\(\sum^n_{j=1}dis(i,j)\)，\(dis(i,j)\)表示\(i\)到\(j\)的最短距离。

• 题解：这\(F\)题比上一题简单的多，也就是计算每个点到根节点的距离之和，假设现在根节点为\(i\)，\(j\)是\(i\)的一个儿子，我们现在知道\(i\)的总贡献\(ans[i]\)，那么\(j\)的总贡献其实是可以\(O(1)\)计算的，具体看图理解：

  

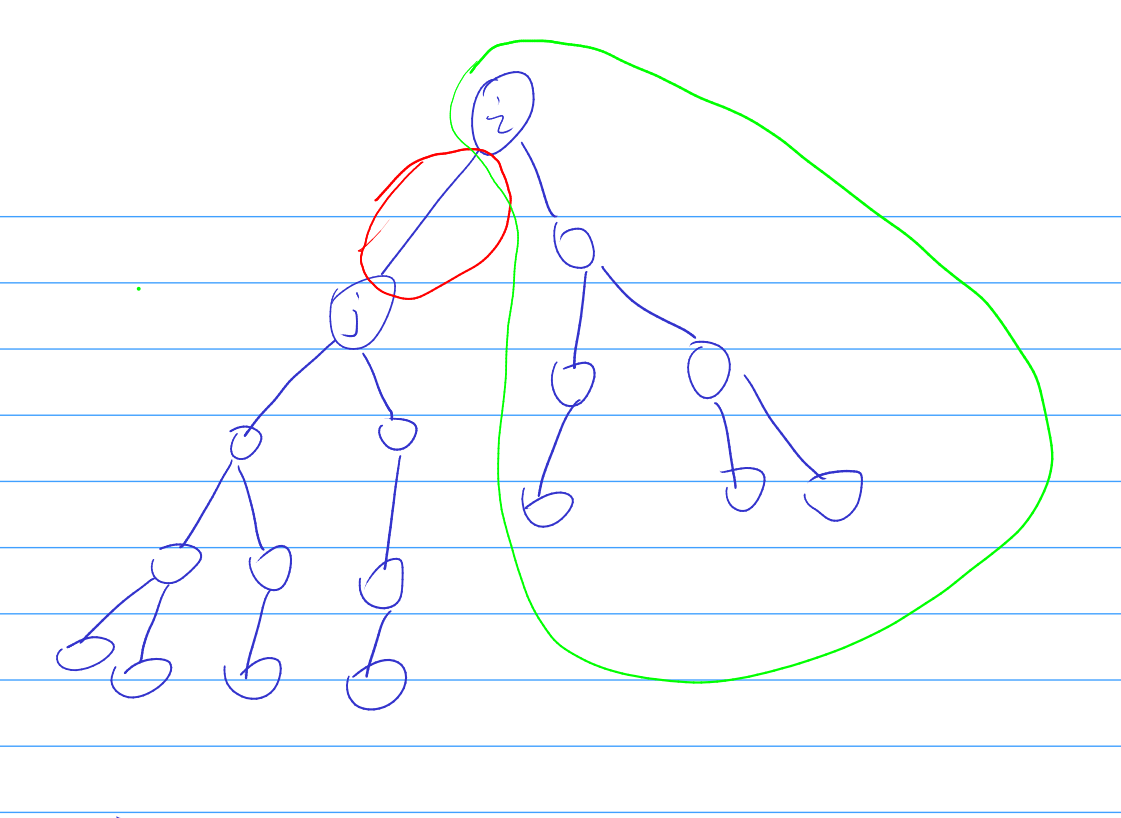
  注意看红色圈起来的那条边，只有这条边造成了贡献的变化，当\(j\)变成根节点后，这条边原本是包含\(j\)在内的其所有儿子的必经之路，即贡献为\(sz[j]\)，但现在根节点变成\(j\)了，这条边的贡献是多余的，给它减去，但是现在这条边是我们绿的这一块部分的必经之路，所以多出的贡献为\(n-sz[j]\)，那么\(j\)的总贡献\(ans[j]=ans[i]-sz[j]+n-sz[j]\).

  所以我们可以先dfs找到\(1\)的总贡献，然后再跑一遍dfs计算每个点的答案。

• 代码：

  #include <bits/stdc++.h>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  #define rep(a,b,c) for(int a=b;a<=c;++a)
  #define per(a,b,c) for(int a=b;a>=c;--a)
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
  ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
  
  int n;
  vector<int> edge[N];
  int sz[N];
  ll ans[N];
  
  void dfs(int u,int fa,int dep){
     for(auto to:edge[u]){
          if(to==fa) continue;
          ans[1]+=dep;
          dfs(to,u,dep+1);
          sz[u]+=sz[to]; 
     } 
     sz[u]++;
  }
  
  void cal(int u,int fa){
      if(u!=1) ans[u]=ans[fa]-sz[u]+n-sz[u];
      for(auto to:edge[u]){
          if(to==fa) continue;
          cal(to,u);
      }
  }
  
  int main() {
      scanf("%d",&n);
      for(int i=1;i<n;++i){
          int u,v;
          scanf("%d %d",&u,&v);
          edge[u].pb(v),edge[v].pb(u); 
      }
      dfs(1,-1,1);
      cal(1,-1);
      for(int i=1;i<=n;++i) printf("%lld\n",ans[i]);
      return 0;
  }