2021牛客暑期多校训练营3 B.Black and white (思维,最小生成树)

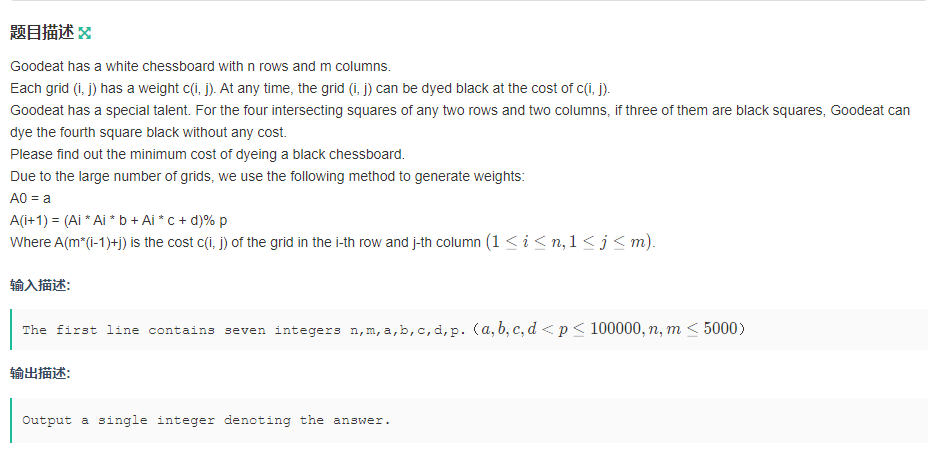
• 题意:有\(n\)x\(m\)的棋盘，将任意一个格子涂成黑色花费\(c_{i,j}\)，任选两行两列，取相交的四个格子，如果其中三个是黑色，则另外一个可以免费涂成黑色，问将整个棋盘涂黑的最小花费.

• 题解:对于任选两行两列取四个格子这个条件，假如我们已经涂了三个格子，那么这三个格子的横纵坐标一定是连通的，假如我们选了第\(1,4\)行,第\(1,5\)列,那么对应的四个坐标为\((A_1,B_1),(A_1,B_5),(A_4,B_1),(A_4,B_5)\),任取其中三个点，再选第四个点时，这个点的坐标一定是在连通块中，也就不用选了，那么这题也就可以抽象成最小生成树，接下来就是一个板子题了。

• 代码：

  #include <bits/stdc++.h>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  #define rep(a,b,c) for(int a=b;a<=c;++a)
  #define per(a,b,c) for(int a=b;a>=c;--a)
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
  ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
  
  int n,m;
  int C[10001][10001];
  int dis[10001];
  bool vis[10001];
  int A[5001*5001];
  
  ll prim(){
      me(dis,0x3f,sizeof(dis));
      ll res=0;
      for(int i=0;i<n+m;++i){
          int t=-1;
          for(int j=1;j<=n+m;++j){
              if(!vis[j] && (t==-1 || dis[t]>dis[j])){
                  t=j;
              }
          }
          vis[t]=true;
          if(i) res+=dis[t];
          for(int j=1;j<=n+m;++j){
              dis[j]=min(dis[j],C[t][j]);
          }
      }
      return 1ll*res;
  }
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
      int a,b,c,d,p;
      me(C,0x3f,sizeof(C));
      cin>>n>>m>>a>>b>>c>>d>>p;
      A[0]=a;
      rep(i,1,n*m){
          A[i]=(1ll*A[i-1]*A[i-1]%p*b%p+A[i-1]*c+d)%p;
      }
      rep(i,1,n){
          rep(j,1,m){
              C[i][j+n]=A[m*(i-1)+j];
              C[j+n][i]=A[m*(i-1)+j];
          }
      }
  
      cout<<prim()<<'\n';
  
  
      return 0;
  }