AtCoder Beginner Contest 207 E - Mod i (dp,优化)
-
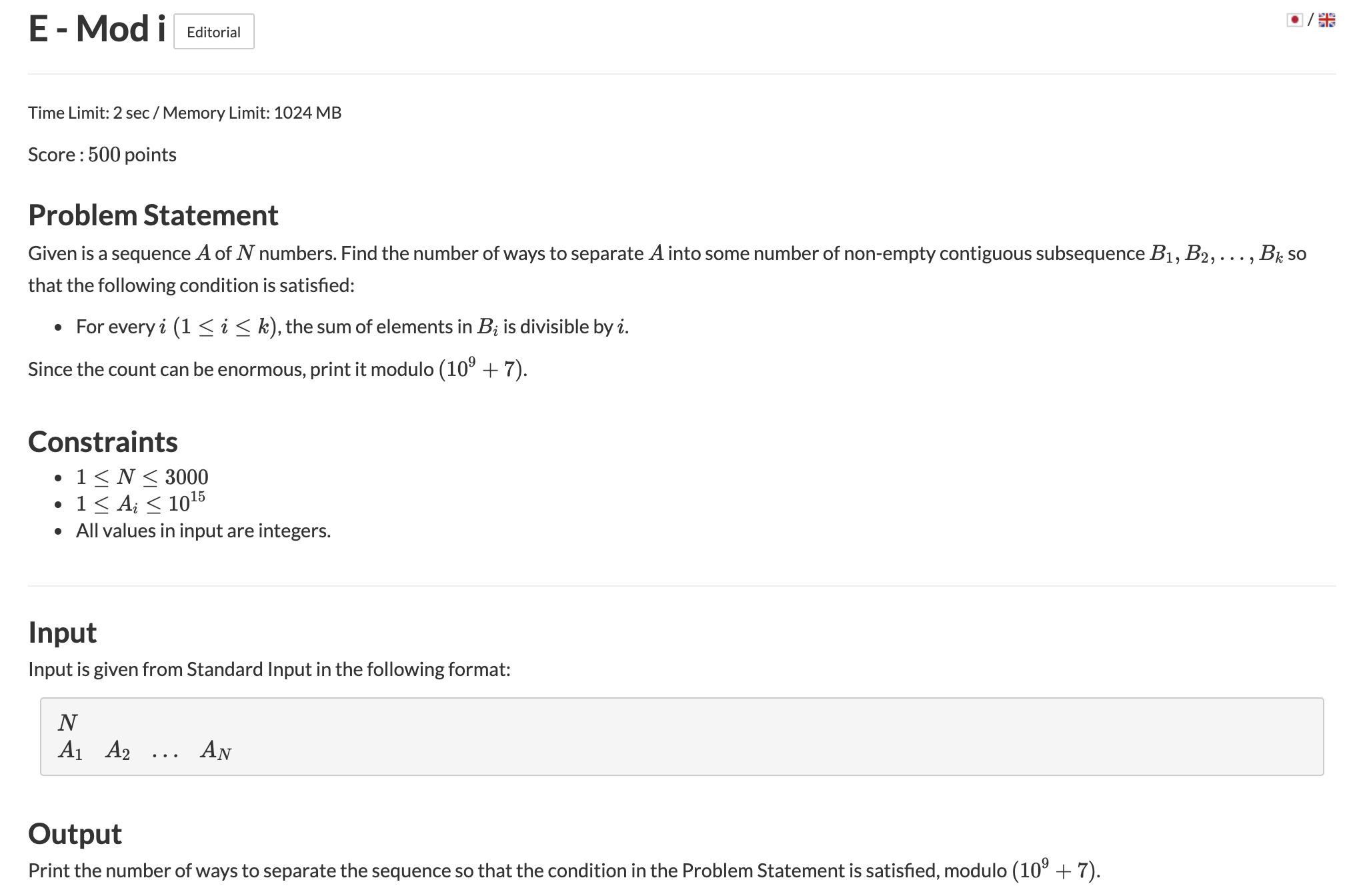
题意:有一长度为\(n\)的序列,问有多少种方式将其分成连续的\(k\)个序列\(B_1,B_2,...,B_k\),使得对于每个\(i\ (1\le i\le k)\)都能整除\(B_i\)的元素和.
-
题解:设\(dp[i][j]\)为取前\(i\)个数分成\(j\)个\(B\)序列的方法数.那么可以写出一个比较暴力的\(dp\)转移式:
\(dp[i][j]=\sum_{k=0}^{i-1}dp[k][j-1]\ only if(sum_i-sum_k\equiv0) \ mod\ j\).这样的复杂度为\(O(n^3)\).
dp[0][0]=1; for(int i=1;i<=n;++i){ for(int j=1;j<=i;++j){ for(int k=0;k<i;++k){ if((sum[i]-sum[k])%j) continue; dp[i][j]=(dp[i][j]+dp[k][j-1])%mod; } } }这样很明显是不行的,我们要进行优化,不难发现,只有当\(sum_i \equiv sum_k\ mod\ j\)的时候才能转移,所以我们可以在最外层枚举\(j\),用桶记录同余的前缀和情况,也就是说我当前的同余值为\(sum_i \ mod \ j\)那么我就要从\(dp[k][j-1]\ (1\le k\le i-1)\)中所有的\(sum_k \equiv sum_i\ mod\ j\)转移过来,这样我们在枚举\(i\)的时候,是可以记录一个\(tot[sum_i \ mod \ j]\)来进行一个前缀优化的,复杂度降到\(O(n^2)\).
-
代码:
#include <bits/stdc++.h> #define ll long long #define fi first #define se second #define pb push_back #define me memset #define rep(a,b,c) for(int a=b;a<=c;++a) #define per(a,b,c) for(int a=b;a>=c;--a) const int N = 1e6 + 10; const int mod = 1e9 + 7; const int INF = 0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; typedef pair<ll,ll> PLL; ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;} ll lcm(ll a,ll b) {return a/gcd(a,b)*b;} int n; ll a[N]; ll sum[N]; ll dp[3005][3005]; ll tot[N]; int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n; rep(i,1,n){ cin>>a[i]; sum[i]=sum[i-1]+a[i]; } dp[0][0]=1; for(int j=1;j<=n;++j){ for(int i=0;i<=n;++i) tot[i]=0; for(int i=0;i<=n;++i){ dp[i][j]=tot[sum[i]%j]; tot[sum[i]%j]=(tot[sum[i]%j]+dp[i][j-1])%mod;; } } ll ans=0; for(int i=1;i<=n;++i){ ans=(ans+dp[n][i])%mod; } cout<<ans<<'\n'; return 0; }
𝓐𝓬𝓱𝓲𝓮𝓿𝓮𝓶𝓮𝓷𝓽 𝓹𝓻𝓸𝓿𝓲𝓭𝓮𝓼 𝓽𝓱𝓮 𝓸𝓷𝓵𝔂 𝓻𝓮𝓪𝓵
𝓹𝓵𝓮𝓪𝓼𝓾𝓻𝓮 𝓲𝓷 𝓵𝓲𝓯𝓮

