AcWing 1010. 拦截导弹 (LIS,dilworth定理)

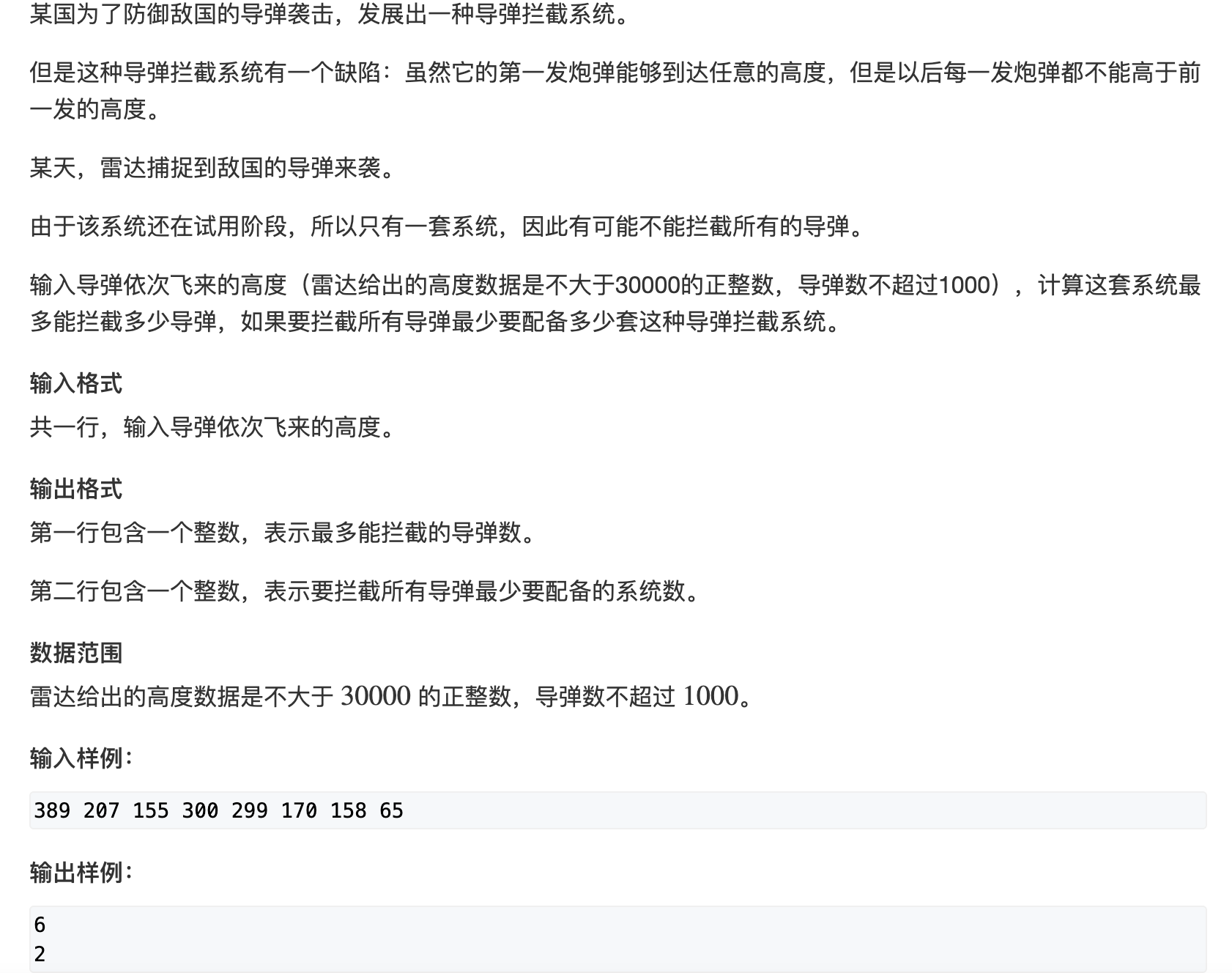
• 题意:给你一组数,求LDS和最少需要多少块LDS

• 题解:第一问LDS随便写,关键是要怎么求出最少有多少个LDS,这里介绍一个dilworth定理:对于任意有限偏序集，其最大反链中元素的数目必等于最小链划分中链的数目.对偶一下,我们要求最小LDS的划分数目,那么也就是求LIS的元素数目.

• 代码:

  #include <bits/stdc++.h>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  #define rep(a,b,c) for(int a=b;a<=c;++a)
  #define per(a,b,c) for(int a=b;a>=c;--a)
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
  ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
   
   
   
  int main(){
      ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
      vector<int> a;
      int x;
      while(cin>>x){
          a.pb(x);
      }
  
      int len=(int)a.size();
      vector<int> dp(len+1);
      int ans1=1;
      rep(i,0,len-1){
          dp[i]=1;
          rep(j,0,i-1){
              if(a[j]>=a[i]){
                  dp[i]=max(dp[i],dp[j]+1);
                  ans1=max(ans1,dp[i]);
              }
          }
      }
      int ans2=1;
      rep(i,0,len-1){
          dp[i]=1;
          rep(j,0,i-1){
              if(a[j]<a[i]){
                  dp[i]=max(dp[i],dp[j]+1);
                  ans2=max(ans2,dp[i]);
              }
          }
      }
  
      cout<<ans1<<'\n'<<ans2<<'\n';
  
      return 0;
  }