P2272 [ZJOI2007]最大半连通子图 (tarjan,拓扑排序dp)

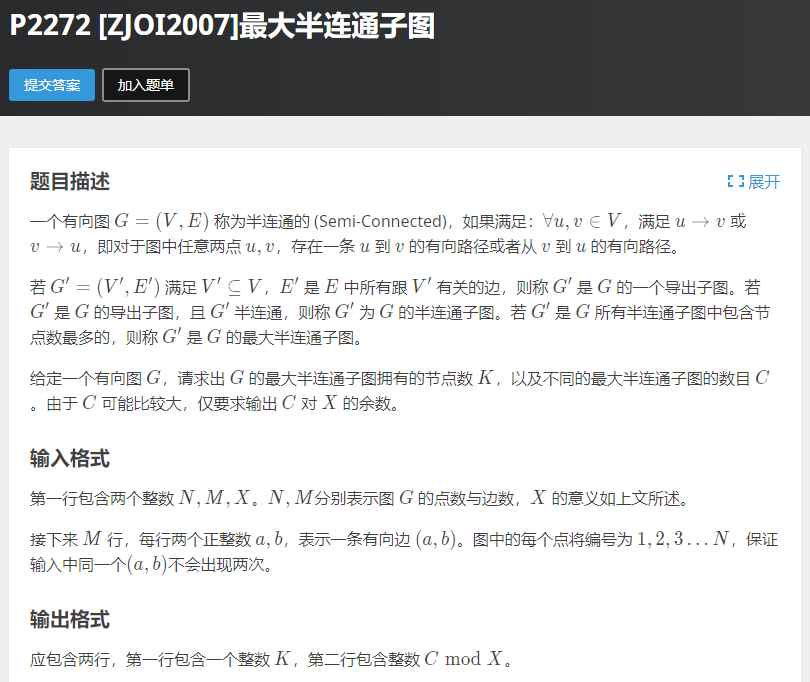
• 题意：给你一个有向图,求最大半连通子图的总节点数和不同最大半连通子图的方案数.

• 题解: 用tarjan缩点后,注意缩点后建边的时候要判重,因为两个连通子图之间可能有很多条边,跑拓扑排序然后dp更新节点数和方案数即可,具体看代码.

• 代码：

  #include <bits/stdc++.h>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  #define rep(a,b,c) for(int a=b;a<=c;++a)
  #define per(a,b,c) for(int a=b;a>=c;--a)
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
  ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
   
  int n,m,x;
  vector<int> edge[N];
  vector<int> new_edge[N];
  int dfn[N],low[N],timestamp;
  int stk[N],top;
  bool in_stk[N];
  int id[N],scc_cnt,sz[N];
  int dp1[N],dp2[N];
  int din[N];
  
  void tarjan(int u){
      dfn[u]=low[u]=++timestamp;
      stk[++top]=u,in_stk[u]=true;
      for(auto w:edge[u]){
          if(!dfn[w]){
              tarjan(w);
              low[u]=min(low[u],low[w]);
          }
          else if(in_stk[w]) low[u]=min(low[u],dfn[w]);
      }
  
      if(dfn[u]==low[u]){
          ++scc_cnt;
          int y;
          do{
              y=stk[top--];
              in_stk[y]=false;
              id[y]=scc_cnt;
              sz[scc_cnt]++;
          }while(y!=u);
      }
  }
   
  int main(){
      ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
      cin>>n>>m>>x;
  
      rep(i,1,m){
          int u,v;
          cin>>u>>v;
          edge[u].pb(v);
      } 
   
      rep(i,1,n){
          if(!dfn[i]) tarjan(i);
      }
  
      unordered_set<ll> s;
      rep(i,1,n){
          dp1[i]=sz[i];
          dp2[i]=1;
          for(auto w:edge[i]){
              int u=id[i];
              int v=id[w];
              ll hash=u*1000000ll+v;
              if(u!=v && !s.count(hash)){
                  s.insert(hash);
                  new_edge[u].pb(v);
                  din[v]++;
              }
          }
      }
  
      queue<int> q;
      rep(i,1,scc_cnt){
          if(!din[i]) q.push(i);
      }
  
      int res=0;
      while(!q.empty()){
          int u=q.front();
          q.pop();
  
          for(auto w:new_edge[u]){
              din[w]--;
               if(dp1[u]+sz[w]>dp1[w]){
                      dp1[w]=dp1[u]+sz[w];
                      res=max(res,dp1[w]);
                      dp2[w]=dp2[u];
                  }
                  else if(dp1[u]+sz[w]==dp1[w]){
                      dp2[w]=(dp2[w]+dp2[u])%x;
                  }
              if(din[w]==0){
                  q.push(w);
                  res=max(res,dp1[w]);
              }
          }
      }
  
      int mx=0;
      int sum=0;
      rep(i,1,n){
          if(dp1[i]>mx){
              mx=dp1[i];
              sum=dp2[i];
          }
          else if(dp1[i]==mx){
              sum=(sum+dp2[i])%x;
          }
      } 
  
      cout<<mx<<'\n'<<sum<<'\n';
      
      return 0;
  }