Codeforces Round #693 (Div. 3) G. Moving to the Capital (图,dp)

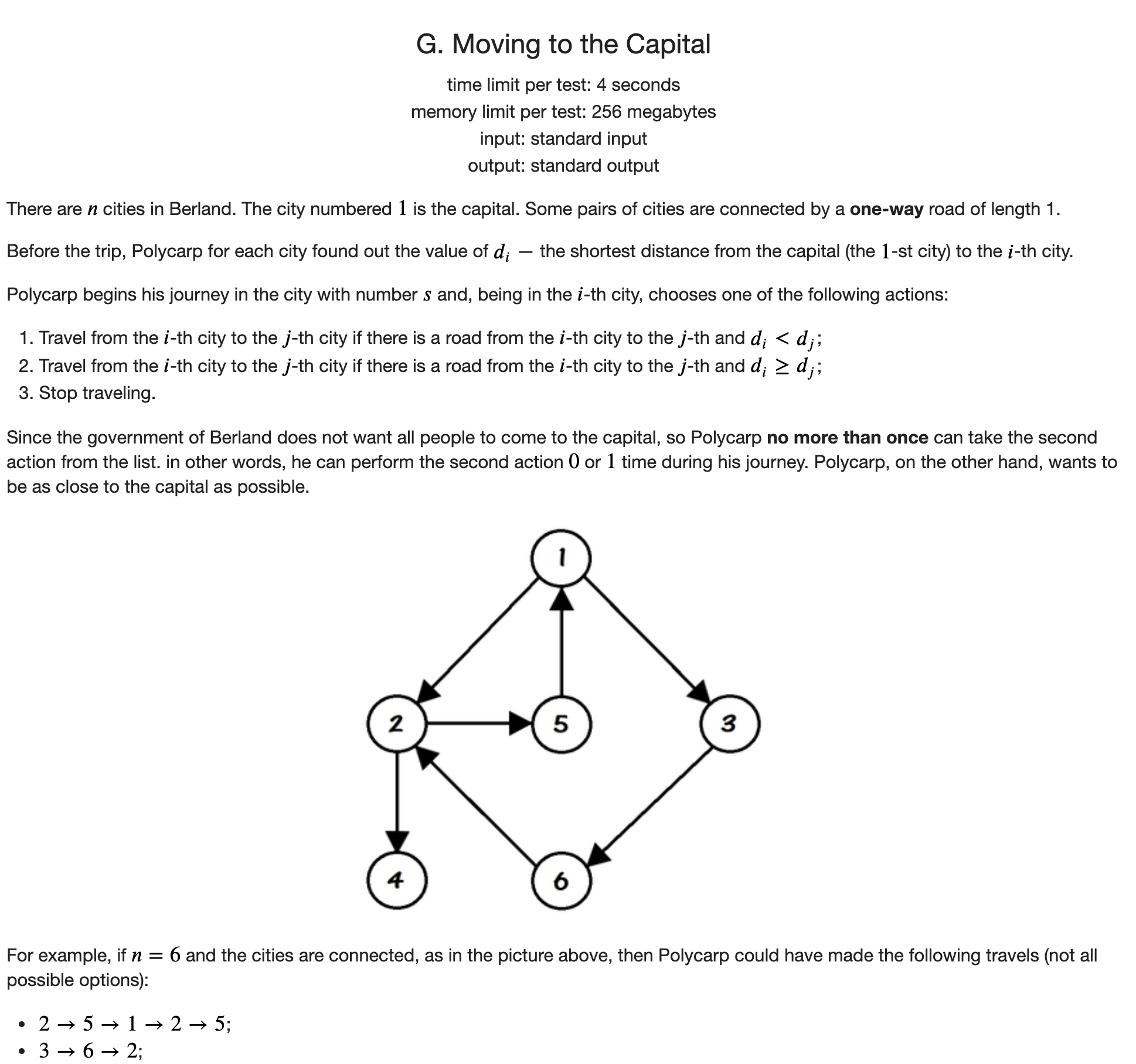
• 题意:有一张有向图,每个点的权值为点\(1\)到该点的最短距离(每条边的长度为\(1\)),对于一条路径,这条路径上最多只能有一条边,这条边起点的权值不小于终点,现在要求每个点能到达路径上的点的最小权值.
• 题解:首先我们先用bfs求出每个点的权值,并且在求的同时用桶将点存起来,方便之后枚举权值的时候用,然后我们可以将权值从大到小枚举,记\(dp_i\)是当前这个点能到达路径上的点的最小权值,对于当前的点\(u\)和它的出边\(v\),如果\(dis[u] < dis[v]\),那么我们是可以继续随便走的,所以当前状态应该是\(dp[u]=min(dp[u],dp[v])\),否则,说明我们将第二次机会用掉了,之后就只能选择第一种操作,所以我们更新的时候就不能将\(dp[v]\)(因为是从大到小枚举,所以\(dp[v]\)的状态一定是已知的)更新给当前状态,因为我们不知道\(dp[v]\)这个状态是否还用了第二次操作,所以当前状态就应该更新为\(dp[u]=min(dp[u],dis[v])\).
• 代码:

#include <bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define me memset
#define rep(a,b,c) for(int a=b;a<=c;++a)
#define per(a,b,c) for(int a=b;a>=c;--a)
const int N = 1e6 + 10;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
using namespace std;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}

int t;

int main() {
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);

	cin>>t;
	while(t--){
		int n,m;
		cin>>n>>m;

		vector<vector<int>> v(n+1);
		vector<vector<int>> tot(n+1);
		vector<int> dis(n+1,INF);
		vector<int> dp(n+1);
		
		int a,b;

		rep(i,1,m){
			cin>>a>>b;
			v[a].pb(b);
		}

		queue<int> q;
		q.push(1);
		dis[1]=0;

		//bfs init
		while(!q.empty()){
			int cur=q.front();
			q.pop();
			for(auto w : v[cur]){
				if(dis[cur]+1<dis[w]){
					dis[w]=dis[cur]+1;
					tot[dis[w]].pb(w);
					q.push(w);
				}
			}
		}

		rep(i,1,n){
			dp[i]=dis[i];
		}	

		per(i,n-1,1){
			for(auto u : tot[i]){
				for(auto w : v[u]){
					if(dis[w]>dis[u]) dp[u]=min(dp[u],dp[w]);
					else dp[u]=min(dp[u],dis[w]);
				}
			}
		}

		rep(i,1,n) cout<<dp[i]<<' ';
		cout<<'\n';

	}

    return 0;
}