AtCoder Beginner Contest 183 E - Queen on Grid (DP)
-
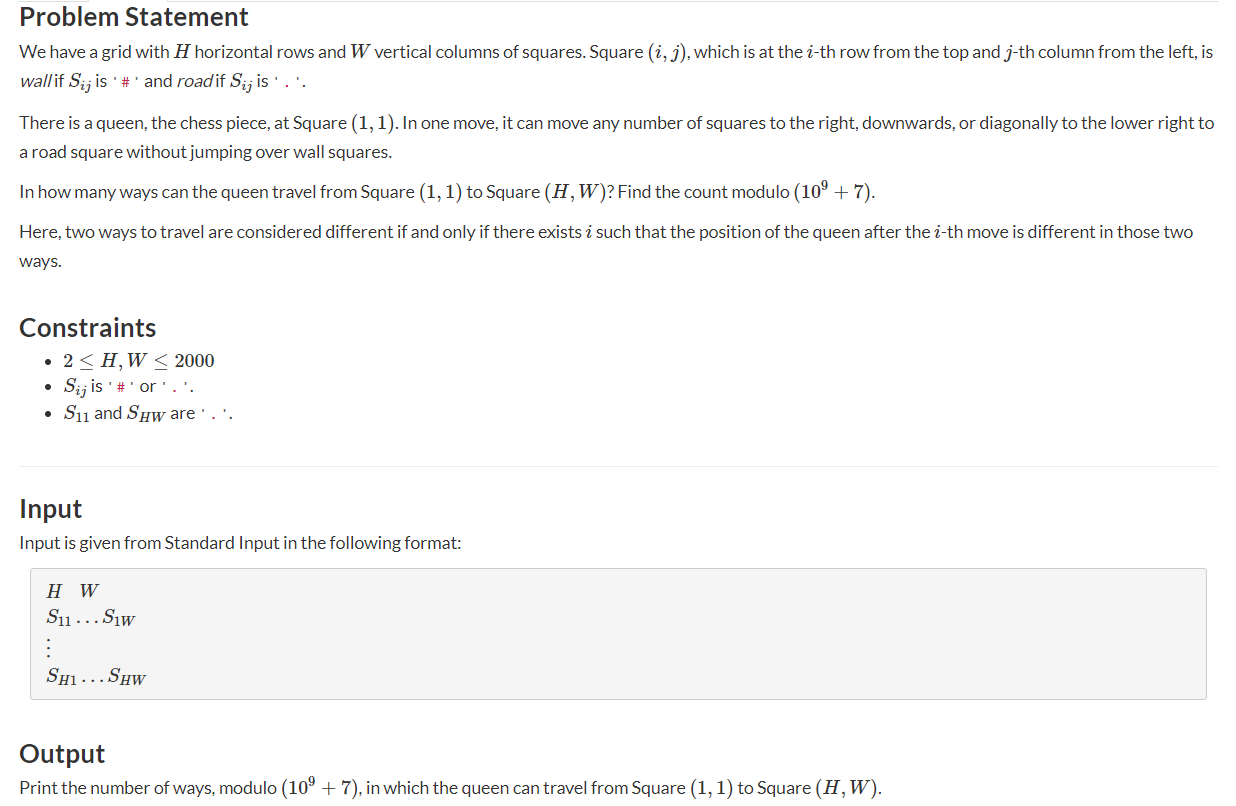
题意:有一个\(n\)x\(m\)的棋盘,你需要从\((1,1)\)走到\((n,m)\),每次可以向右,右下,下走任意个单位,\(.\)表示可以走,#表示一堵墙,不能通过,问从\((1,1)\)走\((n,m)\)的方案数.
-
题解:走棋盘的经典问题的改编,唯一不同的地方在于,棋子可以在某一方向移动任意距离,而某一点的状态可以从上,左上,左三个方向的任意一个\(.\)的点转移而来,所以我们可以记这三个方向的前缀和,然后写出状态转移方程,我们记\(dp[0][i][j]\)为横向的前缀和,同理,\(1\)表示斜向,\(2\)表示纵向,而\(3\)则表示当前点的方案数,假设左方向表示为\(0\),则:\(dp[0][i][j]=dp[0][i-1][j]+dp[3][i-1][j]\),其他两个方向也是同理,求出三个方向的前缀和后再更新当前点的状态,\(dp[3][i][j]=dp[0][i][j]+dp[1][i][j]+dp[2][i][j]\).
-
代码:
#define int long long int n,m; char g[2010][2010]; int dp[4][2010][2010]; signed main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n>>m; rep(i,1,n){ rep(j,1,m){ cin>>g[i][j]; } } dp[3][1][1]=1; rep(i,1,n){ rep(j,1,m){ if(g[i][j]=='.' && i+j!=2){ dp[0][i][j]=(dp[0][i-1][j]+dp[3][i-1][j])%mod; dp[1][i][j]=(dp[1][i-1][j-1]+dp[3][i-1][j-1])%mod; dp[2][i][j]=(dp[2][i][j-1]+dp[3][i][j-1])%mod; dp[3][i][j]=(dp[0][i][j]+dp[1][i][j]+dp[2][i][j])%mod; } } } cout<<dp[3][n][m]<<'\n'; return 0; }
𝓐𝓬𝓱𝓲𝓮𝓿𝓮𝓶𝓮𝓷𝓽 𝓹𝓻𝓸𝓿𝓲𝓭𝓮𝓼 𝓽𝓱𝓮 𝓸𝓷𝓵𝔂 𝓻𝓮𝓪𝓵
𝓹𝓵𝓮𝓪𝓼𝓾𝓻𝓮 𝓲𝓷 𝓵𝓲𝓯𝓮

