动态规划-最长回文串

动态规划：时间复杂度是O(N^2)

Manacher算法，时间复杂度是O(N)

这篇文章主要是想讲怎么样能正确的填二维动态规划的二维表

动态规划比较简单：

　　用一个二维数组，dp[ i ][ j ] 表示 下标 i ~ j 字符串是否是回文的，false or true

　　边界条件是 i - j = 0 , 也就是单个字符必是回文串

　　如果 i - j = 1 ，那么比较 i 和 j 位置上两个字符是否相等，相等的话就是回文的

　　剩余的情况可以根据 如果一个字符串是回文的，那么他两边的字符必定是相等的来推出：
　　dp[ i ][ j ] = dp [ i + 1 ] [ j - 1 ] && (charAt( i ) == charAt( j ))

       即状态转移方程

　

对于长度为N的字符串，需要创建 N * N 大小的数组

但是dp[ i ][ j ] 只有当 i <= j 的情况下才合法（因为总不能逆序得到字符串）

所以只有一半的格子是用到的，而且是以对角线平分

可不可以不使用 Boolean[][] 而使用 boolean[][] 呢？

可以的，只要填表的顺序正确即可

 

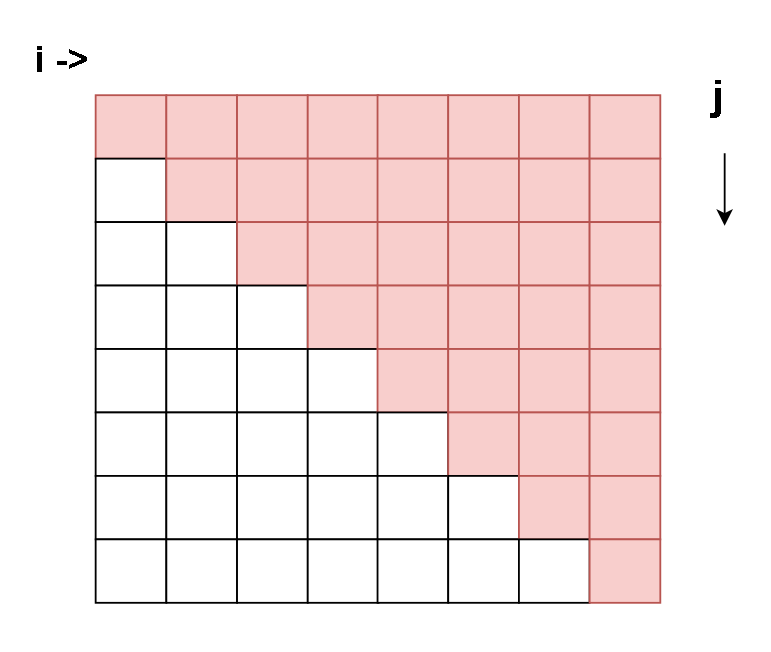
怎么填表呢？

依据状态转移方程， ( i , j ) 位置总是依赖 ( i + 1, j - 1 ) 这个位置，所以只要先把 ( i + 1, j - 1 ) 这个位置先填好就好了

填表路线: 只要是从下往上填就好了，因为如果下一行填好了，上一行一定能使用到左下的格子（空白除外）

 

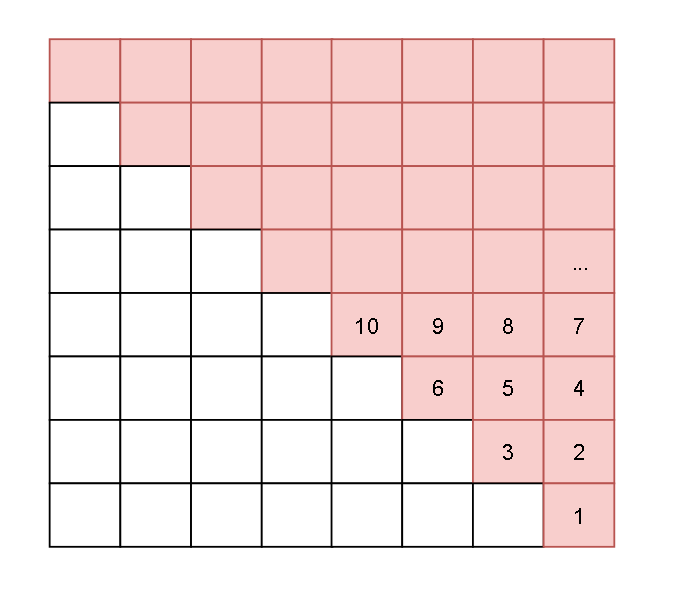
 总结：动态规划的填表顺序可以用二维表格清晰的展示，便于分析