约瑟夫环问题解决方法时间复杂度分析

　　写这篇博客的起因是在牛客上刷到了一道约瑟夫环相关的题。牛客链接

　　在牛客上跑通过了，本着追求机器效率的原则，去leetcode上找到了同样的题，再跑了一遍，发现超时。看了几篇博客并思索许久后打算写这篇博客来探究

约瑟夫环问题在选取不同数据结构和不同处理方法的时候时间复杂度的优劣。leetcode链接

　　关于约瑟夫环及其递推公式请见：https://blog.csdn.net/u011500062/article/details/72855826

　　假设 每数 m 个数就去掉一个人，比如 m = 3，从第一个人开始，则数1,2,3 到第三个人的时候，第三个人消失。

　　公式：当前轮位置为P（P=1，2，3）的人，下一轮的位置 next = (P - m) % 当前轮人数 D

　　　　    有公式： next + k * D  = P - m，所以有 P = m + next + k * D，所以有 P = (m + next + k * D)

　　P % D = ( m + next ) % D，因为 m + next 可能会超出 D，所以需要 % D。以此落到 D 上。其实就是下面的位置+m 然后对上一轮人数取余，就可以得到上一轮的位置

　　需要解释的是为什么受害者之前位置的人在下一轮的下标是（当前下标 - m）% 当前一轮的人数

需要注意的是，当位置P = 0，的时候，代表的是上一轮的最后一个元素。

m = 3

(1 + x) % D 很容易把 x 写成人数 D

 

1 2 3 4 5【（1 + 3）% 5 = 4】

4 5 1 2 【（2 + 3）% 4 = 1】

2 4 5【（2 + 3）% 3 = 2】

2 4 【（1 + 3）% 2 = 0】 这里需要把 0 换成 2，因为当前有两个数，0代表最后一个数

4 

 

 

 

这样算到第

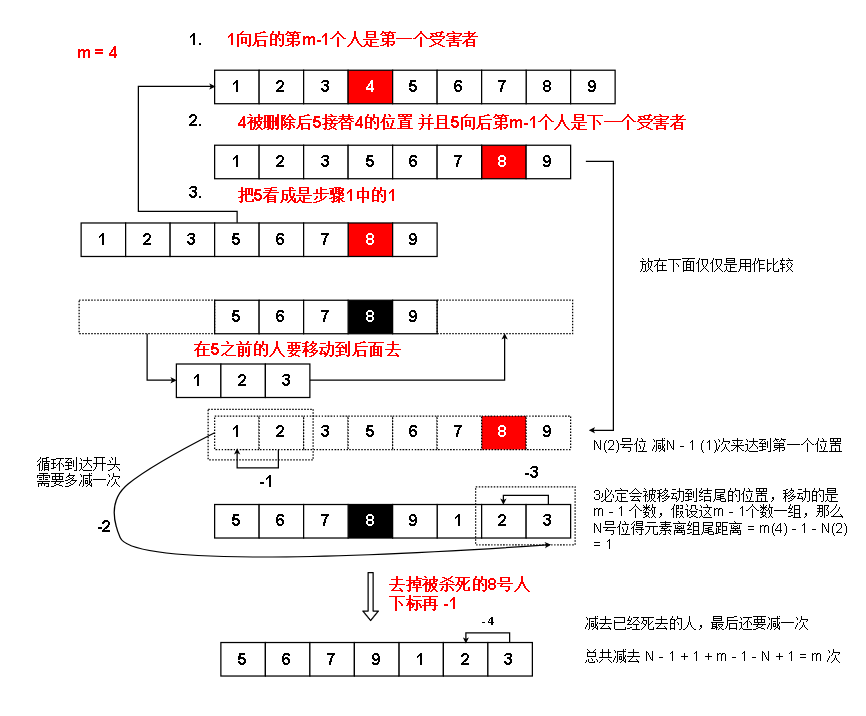
分析时间复杂度：

　　如果要去直接模拟约瑟夫问题的各个环节的话，因为每次都要报数报m次，不考虑具体是什么数据结构实现存储，n个人需要报 n - 1次数，那么问题规模是O(n * m)

　　考虑具体使用的数据结构，比如数组，0号位代表一号人，1号位代表二号人，以此类推，那么有两种方法：

　　　　1.每当有一个人遇害，就把这个人从数组中删去，并且将此人后面的人向前移动。

　　　　2.只是把遇害者的位置标记，不删除该位置，之后访问的时候检查到某个位置的值之前标记过的话就跳过（没有人在这个位置上）

　　第一种情况，总共要挪动多少人 具体是难以推测的，因为每次都是以m为位移在当前数组上找下一个位置，但是可以假设最坏情况，每次移动的人数是当前数组人数 - 1

那么总的移动次数是 ： (n - 1) + (n - 2) + (n - 3) + ...... + 1 = (n - 1) * n / 2 , 是 O（n ^ 2）级的。

　　第二种情况，属于暴力遍历，如果路途中没有遇到之前的遇害者位置，那么访问次数是 m，但是每有一个人遇害，遇害者位置就会 + 1， 所以每次的遍历次数 > m，越遍历下去情况越糟糕，因为人死得越来越多，需要访问-跳过的槽位也越来越多。总次数  > n * m

　　用Java实现：

　　其实第一种情况，对应于使用ArrayList，因为他的底层实现就是数组，并且每次删除元素都会把后面的元素平移。

　　第二种情况，没有什么类似的ADT实现，但是LinkedList有类似之处，LinkedList不能像ArrayList那样直接通过下标找到元素，而是需要一个节点一个节点地next来获取某个

下标位置的元素

　　至于公式推导法......因为是从 2 到 n 遍历，相当于线性时间复杂度 O (n)，真的是数学可以造成降维打击......