分治思想 : 并归排序与其时间复杂度
最近读了吴伟民老师的《数据结构》,学习有感,在此记录
当我们面对规模庞大的问题的时候,往往会一头雾水不知所措
但是如果我们能把这个大问题分解成小一点的问题,再把小一点的问题分解成更小的问题
最终分解成不能再分解的原子问题(Primitive Problem)
如果我们能找到一个通用的方法适用于所有原子问题,那么我们的大问题就迎刃而解了。
这种把大问题分解成小问题来解决(治理) [ Divide And Conquer 我觉得Conquer应该翻译成解决比较好 ] 的方法被称为 ‘ 分治 ’
分治的思想有助于我们解决困难的问题
比如我们要解决一个问题 : 桌子上有八颗大小不同的球,我们要怎么做才能快速地让所有球从小到大(左到右)排序呢?

常规的想法是找到最小的球,和最左边的球交换位置,在找到第二小的球,和左边第二个换位置......
但是,如果采用分治的思想,我们把8颗球看成两组,每组4颗,我们先把每组的顺序排好,再把排好的每一组合并这样,问题小了,好像我们做起来会比较轻松。
把对8颗球排序变为对两组4颗球排序,然后把两组排序后的结果合并,得到我们想要的全部球都有序的结果。
那么对于一组4颗球,我们是否也可以使用同样的思想呢?
把对4颗球排序看成是对两组球,每组2颗球排序,合并两组排序的结果得到4颗球排序的结果
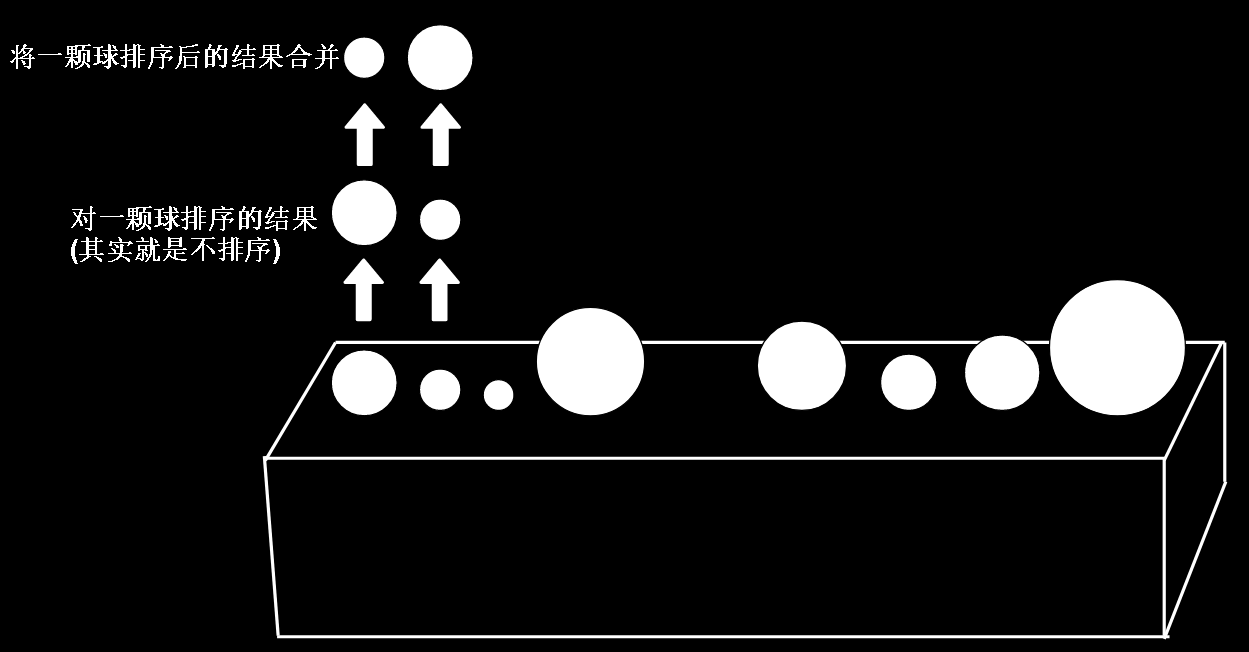
类似的,把对2颗球的排序看作是对两组球,每组一颗球的排序,合并两组排序结果得到2颗球排序结果
最后,只有一颗球了,对一颗球的排序,实际上就是不排序,不会再分解出新的问题,那么,回到上一级问题,也就是对2颗球排序
我们把两组球(每组一颗)的排序结果合并,得到的结果是两颗球有序
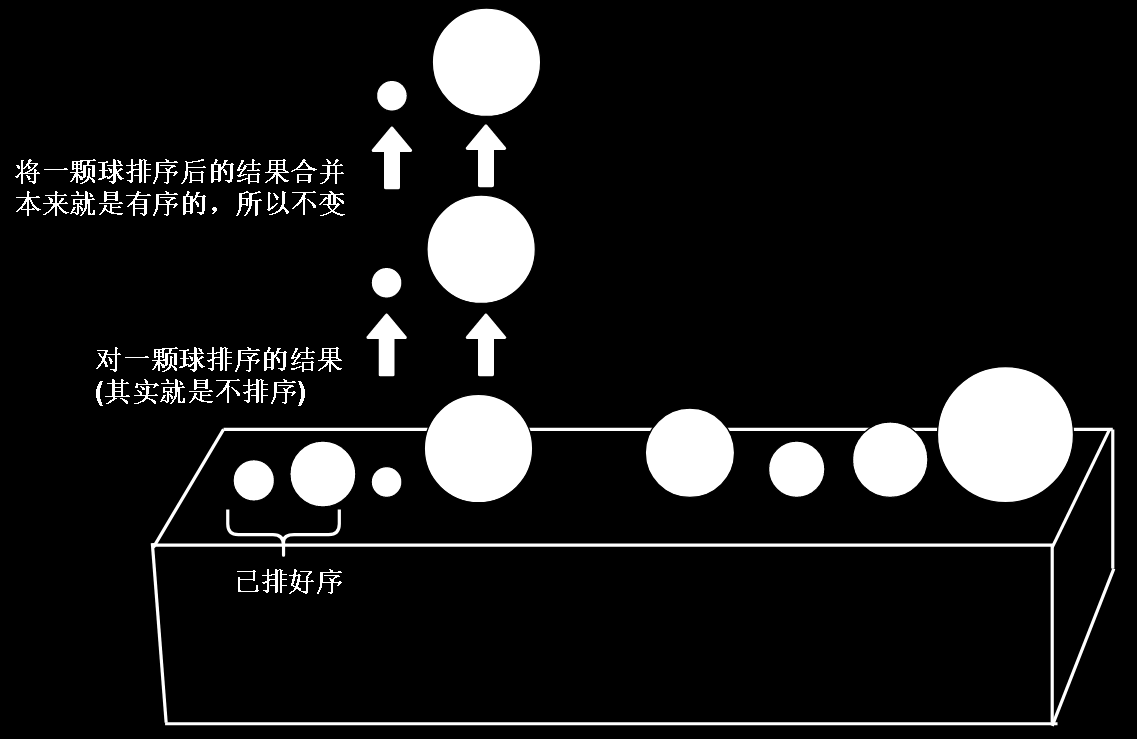

以上就是对两组球(每组两颗)的排序结果,如果我们把这个结果合并起来,就是左边4颗球的排序结果
那么,怎么合并呢?
现在让我们想像一下,有4个槽位,我们要把这两组排好序的球放到这四个槽位里,达成我们给4颗球排序的效果,要怎么放置呢?
也就是要怎么合并这两组球排好序的效果呢?(两颗球排好序 + 两颗球排好序 = 四颗球排好序)

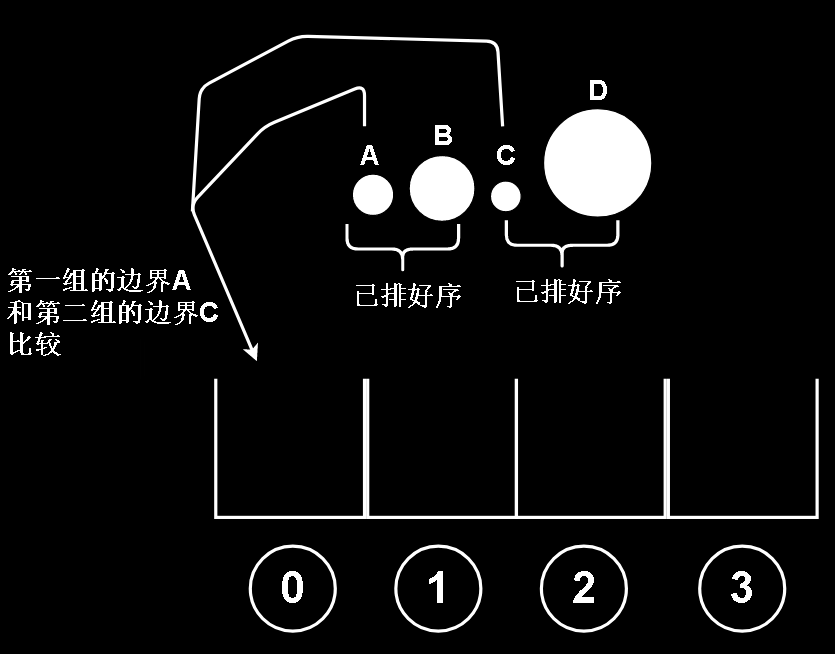
容易想到,我们把两组球的最左边分别比较,为了让描述方便,给这4颗球添加字母识别

因为两组球,组内是有序的,所以只用比较两组的左边界就好了,就能找出两组加起来的所有球中最小的球
并且把这颗球填到最左边还空着的槽里

同理 A 和 D 比较, A 比较小,放入1槽里
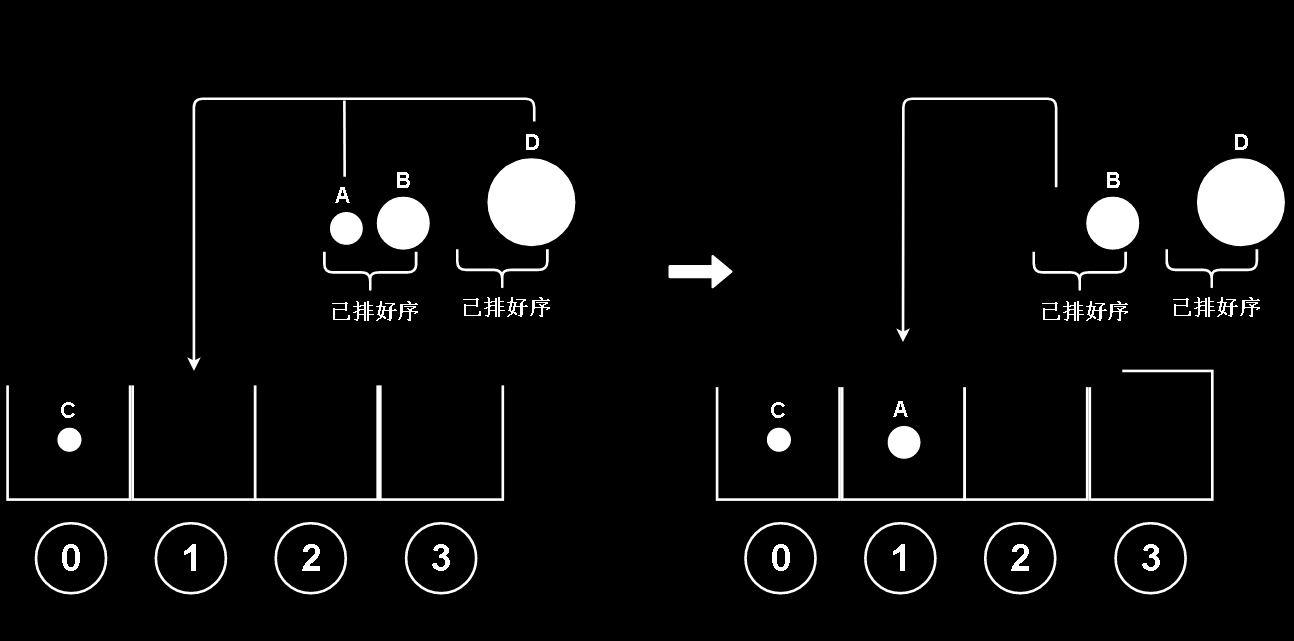
B和D比较也是一样
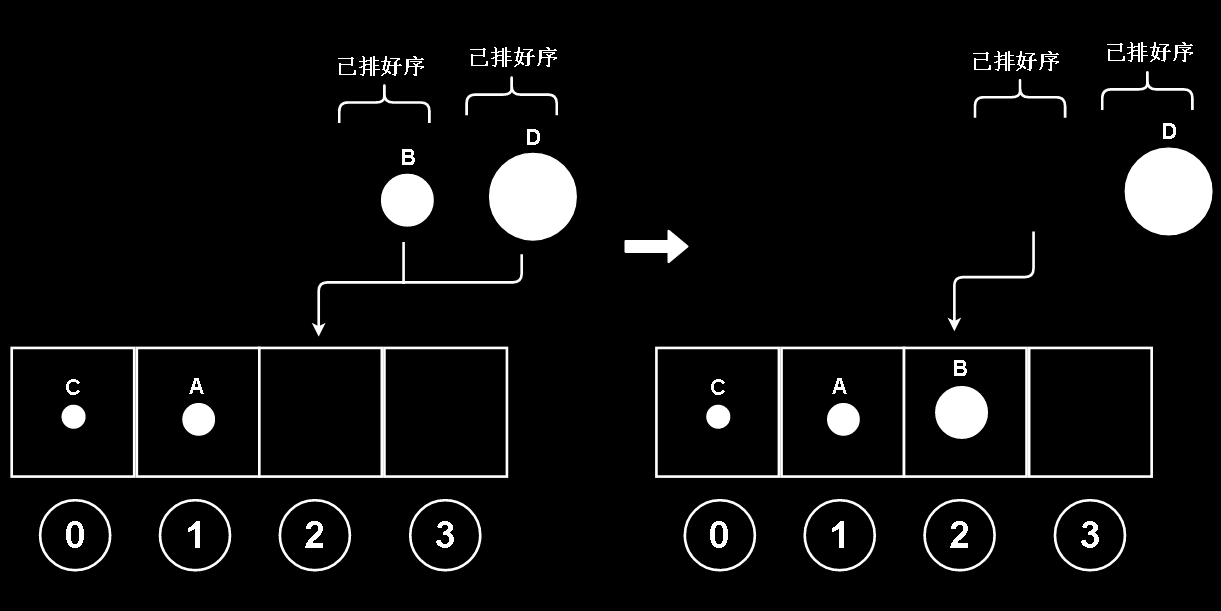
这时,已经有一个组是空的了(左边那一组),没有了最左边界的球可以比较(如果是组里有一个球的话,这个球就是最左边界)
那就把另一组非空的组按左到右顺序加入槽中,当然,因为这里非空组里只剩下D,D理所应当地放入3下标位置
对排序后的两组球(每组两颗)的合并完成,也就是我们得到了4颗球的排序结果

同理地,用上述方法合并两组球(每组4颗)的排序结果,可以得到8颗球的排序结果
基于这个思想,正式引出我们今天要讲的排序算法 , deng deng deng deng ! 归并排序 !
如果我们把刚刚的球换成数字呢?而且是数组中的数字,我们要对数组的排序结果合并。如果刚刚的球和数字等同
那么我们刚刚能放球的空槽等价于什么呢?

显然我们需要一个目标数组来和他等价,用来把排好序的两组数放进去,得到我们想要的结果

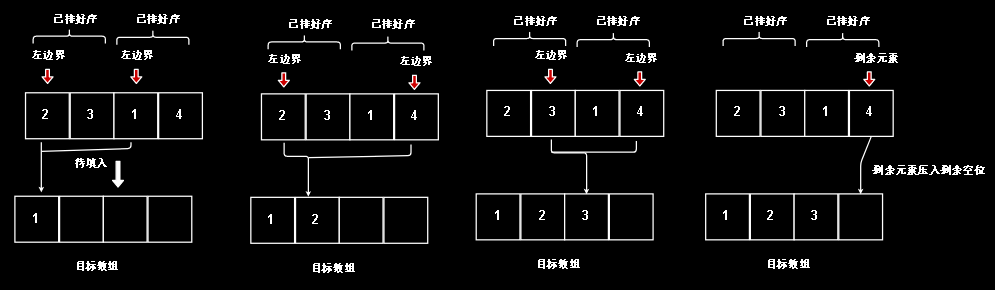
这么一看,好像我们只用把上面那个数组合并到下面那个就够了。合并一次就能达到目的。但如果数据的数量更多,我们会发现不只移动一次
但实际上我们需要在两个数组间进行多次移动
比如我们有一个容量为8的数组,我们想用归并排序对他排序 :

整个过程如下图
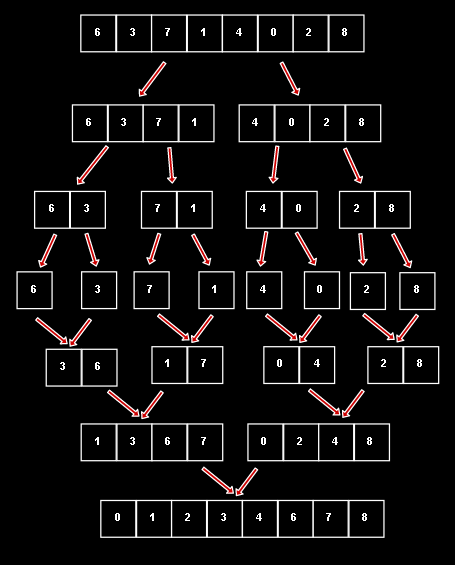
其中合并的过程 :
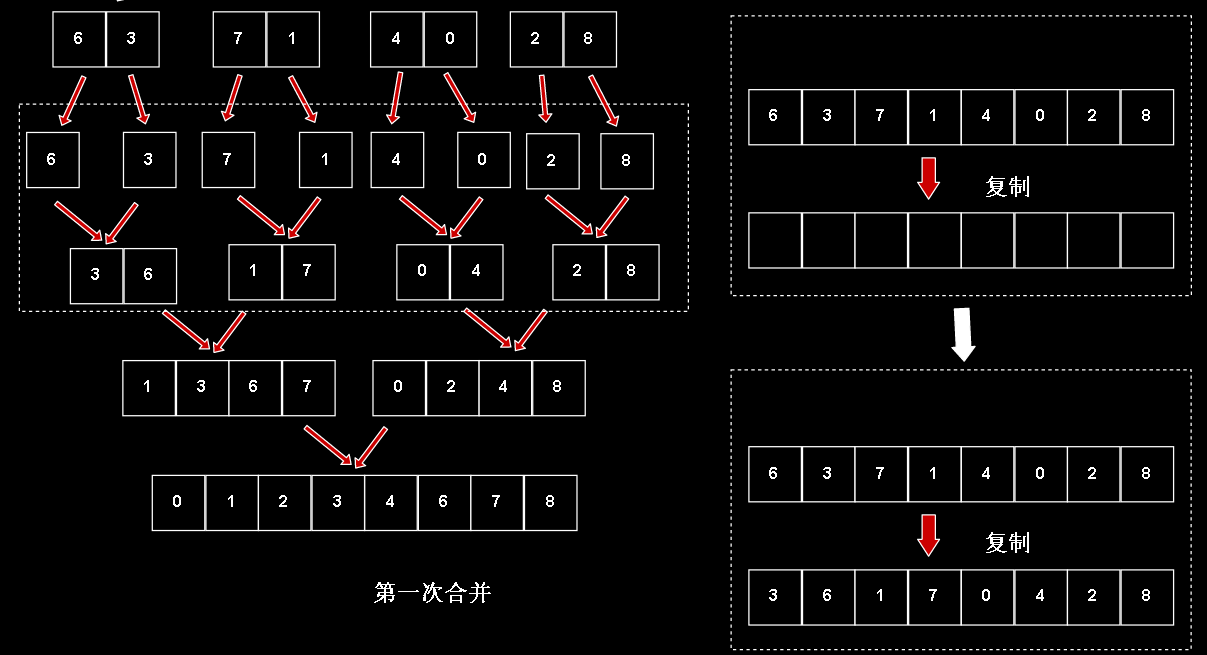


我们发现数据是在上下两个数组间来回复制的,最终合并的结果落在目标数组上,因为我们本来就是想把原数组分成两半,对两半进行排序后
合并到目标数组里。
但有特殊的情况,也就是我们的数组元素个数是奇数的情况
比如说我们对以下数组进行拆分

我们会发现在半分的过程中,有的组拆分次数不一样。
如果我们把整个过程逆过来看,一步一步分析,因为我们希望最后排序完的结果是在目标数组上的的,也就是第一行的数组是在目标数组上的
所以第二行一定是在原数组上,这才符合“把原数组分半,两半的排序结果合并到目标数组”的思想

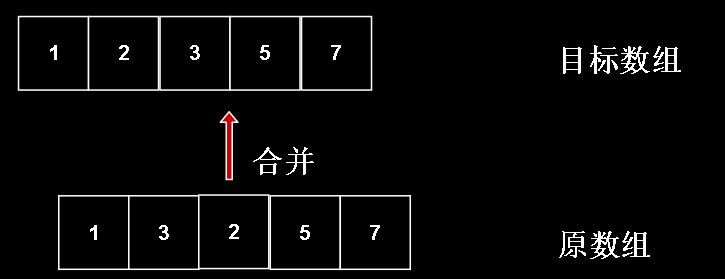
而第二行与第三行则反之,第二行应该是在原数组上,第三行应该是在目标数组上

同理,第四行是原数组,第三行是目标数组,比较特别的是因为第四行只有2和7合并,其他元素还没进行操作,所以我们不画他们
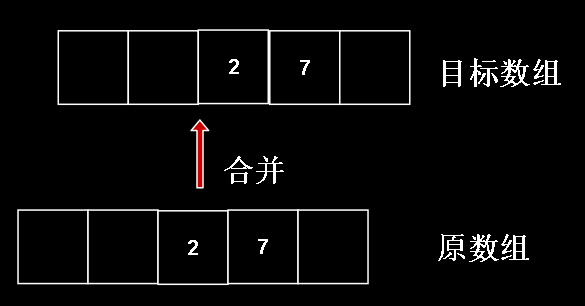
直观一点,我们用手稿画一下,左边被正方形括起来的是‘组’
而没有括起来的是原子(如最后一行的10和-1)

我们发现原子操作 : 对一个数字的排序和合并 就是直接将他复制到另一边,成为一个组
而对原子的复制有两种情况,一种是从原数组到目标数组,也就是倒数第二行
还有一种是从目标数组到原数组,也就是倒数第一行
但是我们发现,从目标数组到原数组的操作实际是空操作,因为原子本来就在我们的原数组里(这时候还没有进行任何操作,原数组还是原来的样子,目标数组处于原始状态),而从原数组到目标数组的原字复制才是实际有操作的,也就是把原子从原数组复制到目标数组对应位置上(倒数第二行)
整个操作只有从上到下合并(原数组到目标数组)和从下到上合并两种操作,如果我们把从上到制标记为0,从下到上标记为1
那么我们一开始的合并(第一行的合并)要标记为0
当我们对原子合并(也就是将原子复制到另一边对应位置),此时的操作标记是0的话,说明确实要复制
而为1的时候,不用复制(对应倒数最后一行)
废话了一大堆,终于要讲代码部分了
如果按照我们刚刚的说法,我们可以先写一下伪代码,伪代码只是一种语义的表示
我们刚刚提到的重要操作有 : 1.合并 2.排序
对这两个操作赋予语义 : 1.Merge 2.Sort
刚刚我们提到,一个大组的排序结果,就是把他分成两个小组,两个小组排序结果的合并
语义 : Sort(Big) = Merge( Sort(Big/2), Sort(Big/2) )
我们想把一个大组从中间分开,而且对分出来的两个组先进行排序,然后合并
语义 :
伪代码 :
Sort(int[] arr, int left, int right){ int mid = (left + right) / 2; Sort(arr, left, mid); Sort(arr, mid + 1, right); Merge(arr, left, mid, right); }
引入目标数组tar
Sort(int[] arr, int[] tar, int left, int right){ int mid = (left + right) / 2; Sort(arr, left, mid); Sort(arr, mid + 1, right); Merge(arr, tar, left, mid, right); }
引入操作标志tag
Sort(int[] arr, int[] tar, int tag, int left, int right){ int mid = (left + right) / 2; Sort(arr, left, mid); Sort(arr, mid + 1, right); Merge(arr, tar, left, mid, right); }
引入对原子的判断
Sort(int[] arr, int[] tar, int tag, int left, int right){ if(left == right){} // 左边界 == 右边界 , 表示当前组只有一个元素,也就是原子 int mid = (left + right) / 2; Sort(arr, left, mid); Sort(arr, mid + 1, right); Merge(arr, tar, left, mid, right); }
引入操作的判断,如果tag是0表示要从原数组复制到目标数组
Sort(int[] arr, int[] tar, int tag, int left, int right){ if(left == right){ if(tag == 0){ tar[left] = arr[left]; }
return; } int mid = (left + right) / 2; Sort(arr, left, mid); Sort(arr, mid + 1, right); Merge(arr, tar, tag, left, mid, right); }
引入操作转换,比如说现在我们的tag是0,那么下一次tag就应该为1
Sort(int[] arr, int[] tar, int tag, int left, int right){ if(left == right){ if(tag == 0){ tar[left] = arr[left]; }
return; } int mid = (left + right) / 2; Sort(arr, tar, tag ^ 1,left, mid);//这里的^ : 0^1 = 1, 1^1 = 0, 起到取反作用,从而使得操作上下交替 Sort(arr, tar, tag ^ 1,mid + 1, right); Merge(arr, tar, tag, left, mid, right); }
这里我们特别注意 : mid = (left + right) / 2;
为什么我们用的是 left, mid mid + 1, right 这种边界分组,而不是 left, mid - 1 mid, right 这种边界分组呢?
假设一下我们的left = a, right = a + 1
也就是 left 和 right 左右边界是相邻的
那么,(left + right) / 2 = (2*a + 1) / 2 = a + 1/2
按照整型省略原则 a + 1/2 = a
那么 如果我们使用 left, mid - 1的话,实际用的是 a, a - 1
mid,right 实际是 a, a + 1 相对我们刚刚的 left, right 边界根本没有变,而且a , a - 1 会让右边界小于左边界!
如果我们使用 left, mid 实际上用的是 a, a
mid + 1, right 实际上是 a + 1, a+ 1 正好满足我们期望中的 left == right 的条件!
这是我们常见的,对线性结构分区时的边界细节。
上述就是我们的并归排序的大体伪代码,可以看出来是一个递归实现
但是还有一点,我们的Merge函数还没实现呢!
其实很简单,也就是把一个数组两个连续区域的元素按顺序加入到另一边的数组里
也就是我们上面讲过的一个图 :
回顾一下 :

Merge函数的arr参数就是上面的那个数组,原数组,而tar则是下面的数组,目标数组,而left指的是左边小组的左边界(2所在位置),mid指的是中间

因为我们刚刚指明了

左边小组是从 left 到 mid,右边小组是从 mid + 1 到right
所以mid 指的是上述的 3元素所在位置下标,而 mid + 1 则是1元素所在位置下标
mid 是左边小组的右边界,而mid + 1是左边小组的左边界
tag 用来判断并轨操作是要从上到下还是从下到上
那么我们来实现一下图中的过程:
首先要用两个变量来遍历左右两个小组,比较左右两个小组当前元素的大小,小的放到另一边的数组里
定义左边小组的边界变量为 j,右边小组的边界变量为 k,变量 i 用来记录现在我们要放东西进去的数组放到第几个位置了
因为我们上面讨论了,元素是在两个数组间复制来复制去的,所以要放东西过去的数组不一定是我们的原数组,也不一定是目标数组
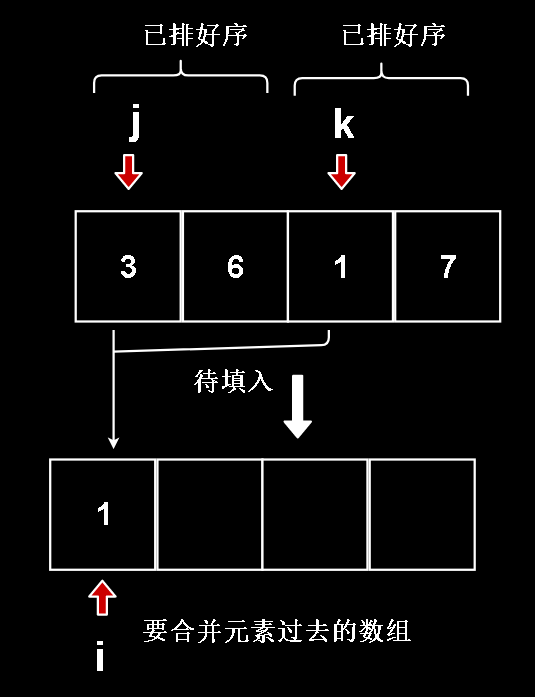
Merge(int[] arr, int[] tar, int tag, int left, int mid, int right){ int i, j, k; }
接着,既然我们知道数组之间复制来复制去,那么直接按照 tag 来判断到底谁是要被放元素进去(也就是把并归结果放进去)
Merge(int[] arr, int[] tar, int tag, int left, int mid, int right){ int i, j, k; if(tag == 1){ int[] temp = arr; arr = tar; tar = temp; } }
函数头中
Merge(int[] arr, int[] tar, int tag, int left, int mid, int right)
arr 是MergeSort放进来的,只能是原数组,而 tar 只能是目标数组
但是我们为了方便直接认定 arr 是被并归的数组,而 tar 是要被放并归结果的数组,反正函数的引用形参交换不会影响外部引用实参(如果是JAVA )
并且直接用 tag 来认定谁是 arr , tar,也就是被并归数组和接受并归结果的数组
如果 tag 是 1,说明是从原本的目标数组 tar 并归到 arr,那么 tar就是被并归的数组,让 arr 指向他
原本的 arr 是接受并归结果的数组,所以把他设置成 tar,这样只是图方便简洁,其实交换还是会降低一定效率的。
再来是,引入两组待合并数组的边界比较部分,两组的边界元素比较后,小的那个会放入 tar 里
Merge(int[] arr, int[] tar, int tag, int left, int mid, int right){ int i, j, k; if(tag == 1){ int[] temp = arr; arr = tar; tar = temp; } for(i = left,j = left, k = mid + 1; j <= mid && k <= right; i ++) { tar[i] = arr[j] < arr[k] ? arr[j ++] : arr[k ++]; } }
最后,是将剩下的元素压入 tar ( 如果一个组已经被移入 tar 移空了,那么另外一组剩下的就可以直接放入 tar 了,反正已经有序了)
Merge(int[] arr, int[] tar, int tag, int left, int mid, int right){ int i, j, k; if(tag == 1){ int[] temp = arr; arr = tar; tar = temp; } for(i = left,j = left, k = mid + 1; j <= mid && k <= right; i ++) { tar[i] = arr[j] < arr[k] ? arr[j ++] : arr[k ++]; } while(j <= mid){ tar[i ++] = arr[j ++]; } while(k <= right){ tar[i ++] = arr[k ++]; } }
上面这些不像伪代码的伪代码,写成Java的形式:
//调用 mergeSort 对 arr 数组排序后,arr 并不是有序的, 而 tar 才是有序
public void mergeSort(int[] arr, int[] tar, int tag, int left, int right){ if(left == right){ if(tag == 0){ tar[left] = arr[left]; } return; } int mid = (left + right) / 2; mergeSort(arr, tar, tag ^ 1,left, mid);//这里的^ : 0^1 = 1, 1^1 = 0, 起到取反作用,从而使得操作上下交替 mergeSort(arr, tar, tag ^ 1,mid + 1, right); merge(arr, tar, tag, left, mid, right); } public void merge(int[] arr, int[] tar, int tag, int left, int mid, int right){ int i, j, k; if(tag == 1){ int[] temp = arr; arr = tar; tar = temp; } for(i = left,j = left, k = mid + 1; j <= mid && k <= right; i ++) { tar[i] = arr[j] < arr[k] ? arr[j ++] : arr[k ++]; } while(j <= mid){ tar[i ++] = arr[j ++]; } while(k <= right){ tar[i ++] = arr[k ++]; } }
现在我们可以计算一下并归排序的时间复杂度
归于递归实现的算法,时间复杂度一般可以用消去法得出
首先,对于一个规模为 n 的问题,我们知道我们主要做了三件事

1.左半边小组归并排序
2.右半边小组归并排序
3.并归
那么对于规模 n 的问题 并轨排序耗时的表达式为 :
T ( n ) = 2 * T ( n / 2 ) + Tm( n )
其中 T ( n ) 是归并排序对规模为 n 的问题的耗时 , Tm ( n )是归并操作对一个规模为 n 的问题的耗时
其实容易得出 Tm ( n ) = n 因为整个归纳操作只是线性的扫描两个数组,让后把他们线性地放入到接受并归结果的数组,真正耗时可能为 k * n , 但是
算时间复杂度一般把常数 k 省略, 因为当 n 极大时,k << n , 可以忽略
则 T ( n ) = 2 * T ( n / 2 ) + n
我们把 两边同时除以 n,会发现等式两边出奇对称
T ( n ) / n = [ 2 * T ( n / 2) / n ] + 1 =[ T ( n / 2) / ( n / 2 ) ] + 1
设 An = T(n) / n
则 An = A(n/2) + 1
A(n/2) = A(n/4) + 1
A(n/4) = A(n/8) + 1
A(n/8) = A(n/16) + 1
......
A(2) = A(1) + 1
把上述所有公式的左边全部加和等于右边全部加和
我们发现 第一行右边的 A(n/2) 可以和第二行左边的 A(n/2) 消去,第二行右边的 A(n/4) 可以和第三行左边的 A(n/4) 消去 ......
最后可以得出 An = A(1) + (log2)(n) = T(1)/1 + (log2)(n) = T(n)/n
最终把 T(n)/n 的 n 乘到左边,得到 T(n) = n*T(1) + n * (log2)(n) = n * 1 + n * (log2)(n)
从极限的角度看,可以把 n 约去
也即 T(n) = n * (log2)(n) ,
可以看出归并排序的时间复杂度是 n * logn 级别
实际上,我们整个排序过程的耗时操作几乎都花在并归上,因为我们的 MergeSort() 总是将排序委托给下一组
而且到了最后的 MergeSort 直接对原子进行复制就好了,根本没有排序
而每将数组分一半都要进行一次并归,如果我们的数组能分成两半,那么只要并归一次
如果我们的数组能分成四半,那么要并轨两次,如果我们的数组是大小接近 2 ^ n , 那么要并归 n 次
反过来,如果我们的数组大小是 n,那么要并归 (log2)(n) 次,而每次并轨的都是线性操作,也就是每次并轨的长度总是总长度的 n / k
如果 n >> k ,那么我们可以近似地认为每次并归的长度都是 n ,这样最后的时间复杂度是 n * (log2)(n) 级别, 也就是 n * logn 级别
但是实际上,并归排序需要一个额外的数组,一个额外的存储空间,对于小内存机器,这无疑是致命的,尤其是对单片机之类的没有磁盘,无法内存换页IO的机器
当数据量十分庞大,整个机器可能因为没有足够的内存而瘫痪,所以在实际应用中,我们一般不会使用归并排序,而是使用 时间复杂度同时 n * logn(一般情况下),而空间复杂度
是 O(1) 的快速排序




