算法复习 : 插入排序原理,记忆,时间复杂度 (7行java实现)
最近啃了一遍吴伟民老师的《数据结构》,记录一些心得。
一种简洁的插入排序 :
1.重要概念 : 哨兵
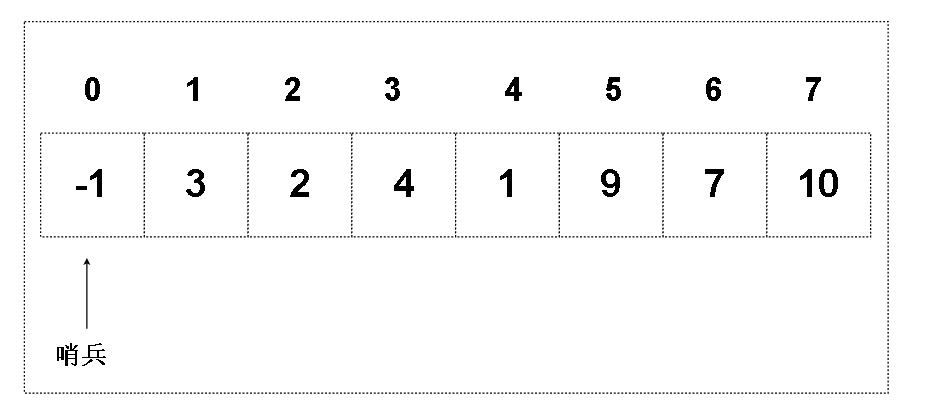
1.在我们要排序的数组中,哨兵做为一个辅助的位置,一般是0下标的槽位做为哨兵
2.哨兵位置上记录的数据不是有效的数据,而是临时的数据,比如上面的 ‘ -1 ’就是一个临时数据,具体的怎么个‘临时’法,请看等下的排序过程分析
3.用哨兵的好处 : 在比较过程中,可以减少边界判断条件,无需判断下标是否小于0,书上的解释也将哨兵称为‘监视边界的哨兵’(请看稍后下方的演示)
4.坏处 : 占用了一个槽位的空间,这个槽位除了排序平时是没有用的,但如果我们的数据量远大于1的话,这个空间其实也不是那么重要,尤其是在内存容量较大的情况下
排序过程 :
1.首先我们定义一个遍历 i 来控制数组的遍历,因为0下标是哨兵,所以我们的 i 从 1 开始
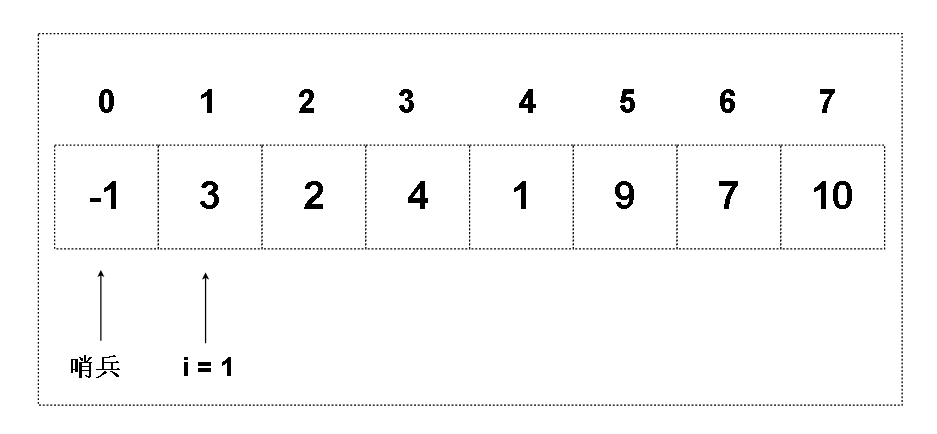
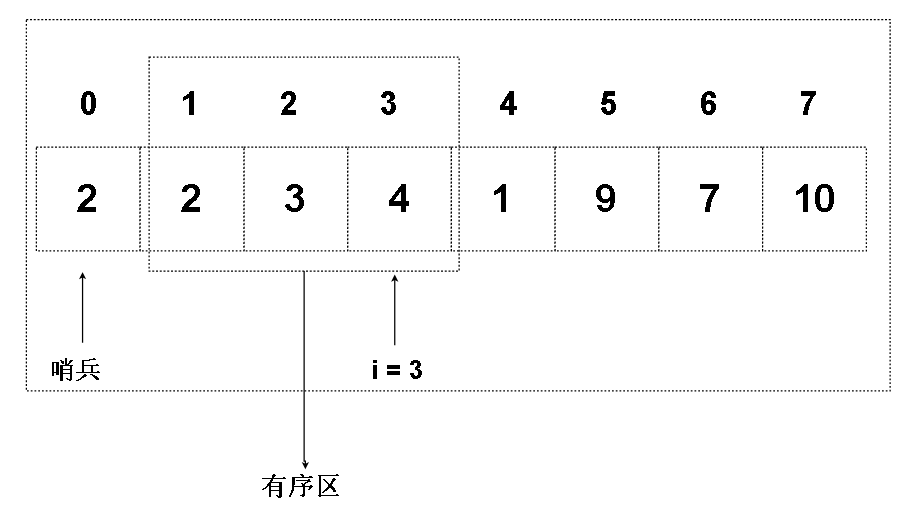
我们需要做到的是,i 遍历的过程中,i 指向的下标位置及其左边区域必须都是有序的(除了哨兵),这一片左边的区域被称为有序区。
比如我们遍历过程中, i = 3时,3下标位置及其左边的区域(1, 2下标区域, 哨兵的0下标位置不算)已经是有序的了,我们的目标就是扩大这个有序区,最终让整 个数组有序
按照我们刚刚说的,我们需要先定义一个 i 变量去遍历数组,并且这个遍历从1开始(因为0是哨兵)
public void insertionSort(int[] arr){ for(int i = 1;){ } }
假想我们手里有一副牌,我们知道我们想把手上的牌整成顺序的话,4比9小,比有序的区域小,所以我们知道要把它插入到左边某个位置
但如果不是4而是10呢,我们发现它比9大,所以不移动,有序区加上我们这张10也是有序的。
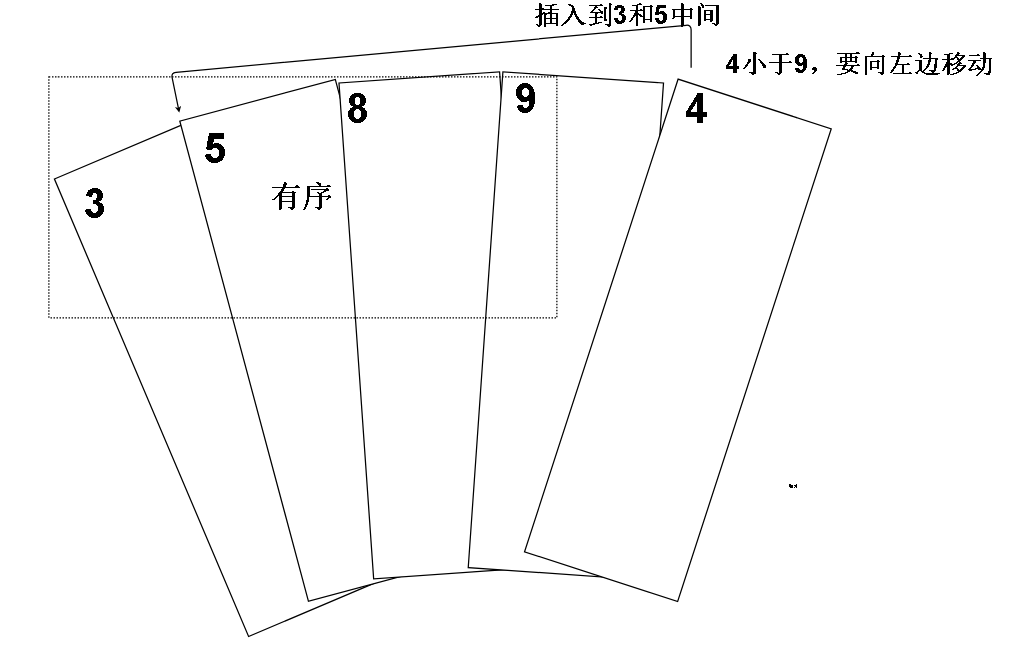
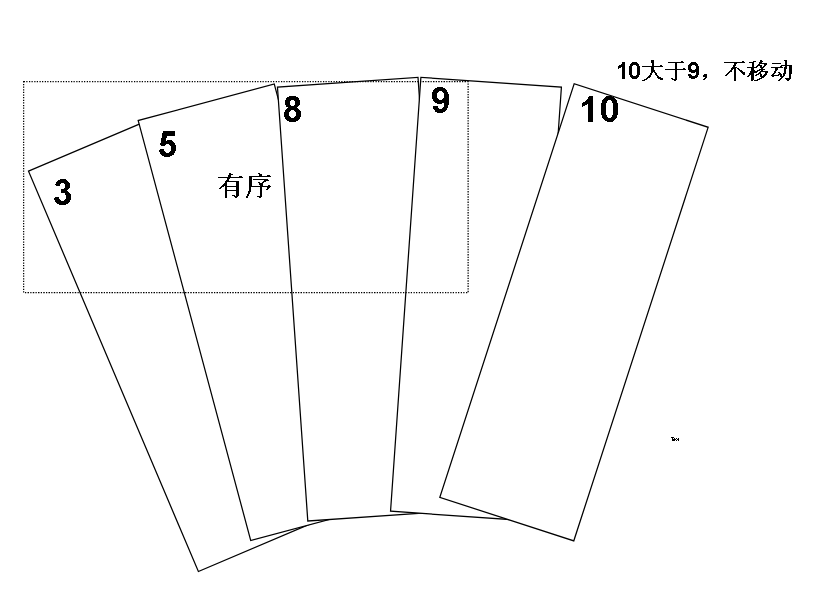
类似的,每次 i + 1 下标的元素都会和 i 下标的元素比较(也就是无序区的左边界和有序区的右边界比较),如果 i 下标元素比较大,那么说明有序区的最大值(假设有序区从小到大),比将要加入有序区的元素大,说明要加入的元素必须往前插。
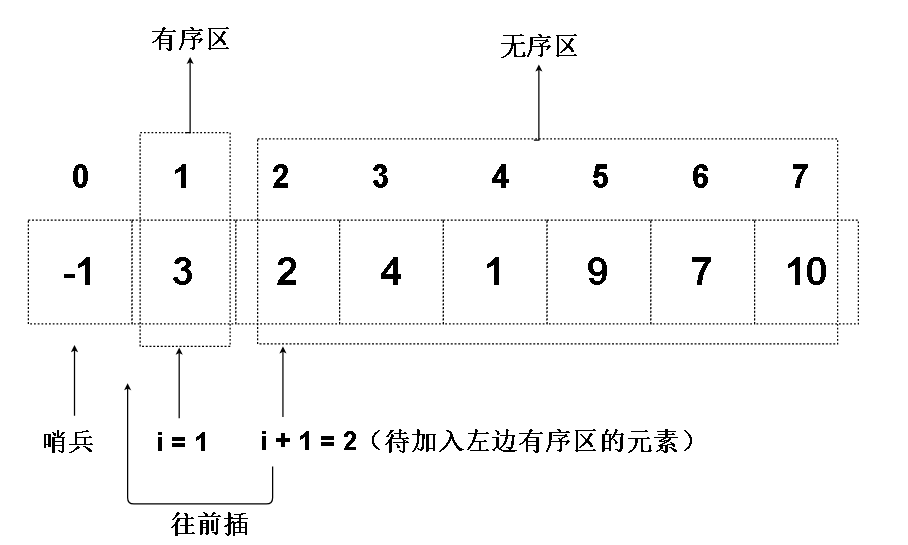
丰富我们的代码 :因为用到 i + 1, 而 i + 1 <= length - 1 , 所以 i <= length - 2
public void insertionSort(int[] arr){
//i < arr.length - 1 也就是 i <= arr.length - 2 for(int i = 1; i < arr.length - 1; i ++){ } }
接下来是加入比较部分 :
public void insertionSort(int[] arr){ //其中的j是临时变量用来保留 i + 1,以及之后标记空位,请向下看
int j;
//i < arr.length - 1 也就是 i <= arr.length - 2 for(int i = 1; i < arr.length - 1; i ++){ if(arr[(j = i + 1)] < arr[i]){ } } }
这时候哨兵的功能就要发挥了,我们把 i + 1 位置的元素存在哨兵里
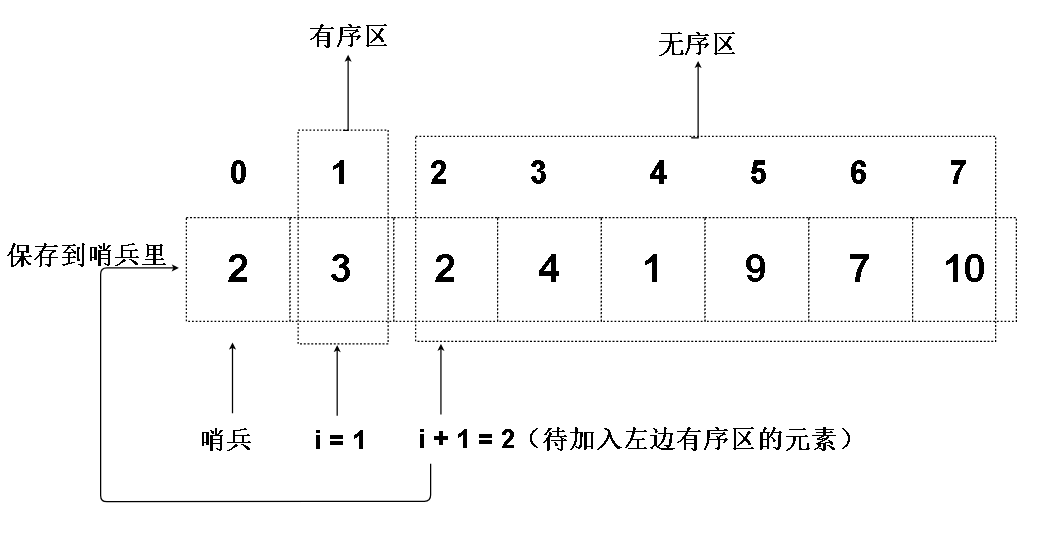
代码添加如下 :
public void insertionSort(int[] arr){ int j;
//i < arr.length - 1 也就是 i <= arr.length - 2 for(int i = 1; i < arr.length - 1; i ++){ if(arr[(j = i + 1)] < arr[i]){ //设置哨兵 arr[0] = arr[j]; } } }
哨兵位置的元素(也就是原来i + 1 位置的元素),比 i 位置的元素小,所以 我们确定了 应该是哨兵在左边,i 位置元素在右边 ,所以 i 位置元素先覆盖 i + 1 位置,但是哨兵元素插不插入到 i 位置还不知道,因为 i 位置后面的元素可能比哨兵大。

代码先加入覆盖部分,上述的描述可能比较复杂,下面有对应的图解
public void insertionSort(int[] arr){ int j;
//i < arr.length - 1 也就是 i <= arr.length - 2 for(int i = 1; i < arr.length - 1; i ++){ if(arr[(j = i + 1)] < arr[i]){ //设置哨兵 arr[0] = arr[j]; do { //j = i + 1, j - 1 = i arr[j] = arr[j = j - 1]; //覆盖后 j = i } } } }
图解 :
就像我们的一副牌,我们知道4要往左边插,那我们先把他放在一边
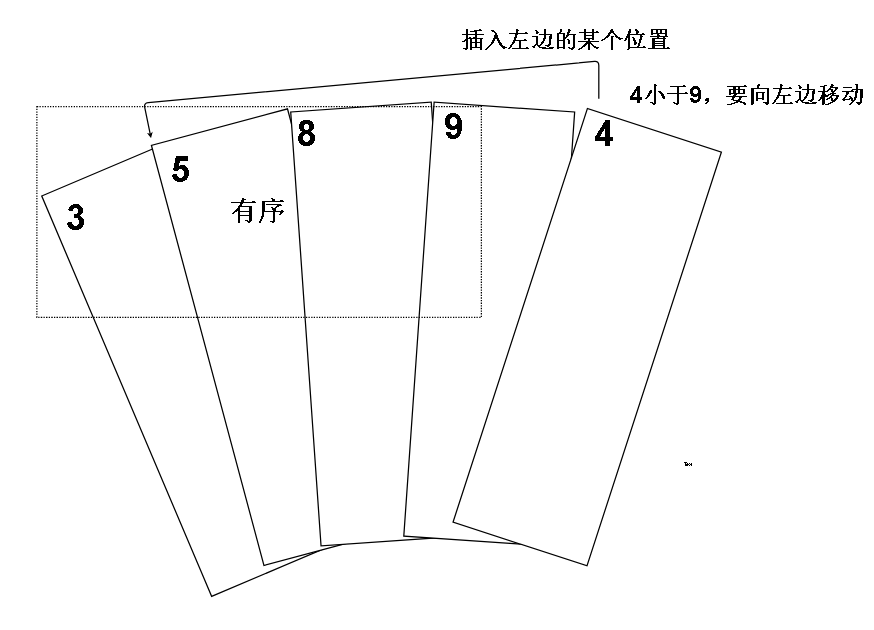

我们发现9比4大,那么把9往右边挪一挪,也就是上述的 i 位置元素覆盖了 i + 1 位的元素
但是4能直接插入到8和9中间(也就是 i 下标位置)吗?答案是不能,因为右边的8,5还比4大!所以我们的4,也就是哨兵,还要和左边继续比较
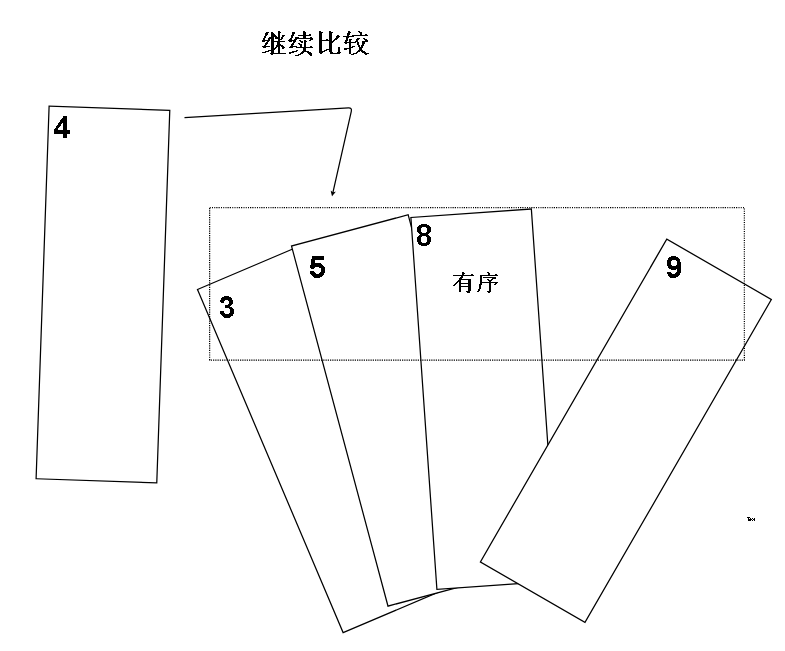
什么时候停止比较呢?

假如我们设上述的空位下标为 j,那么空位后面那个需要和哨兵(也就是上图我们抽出来的牌4)位置就是(j - 1)
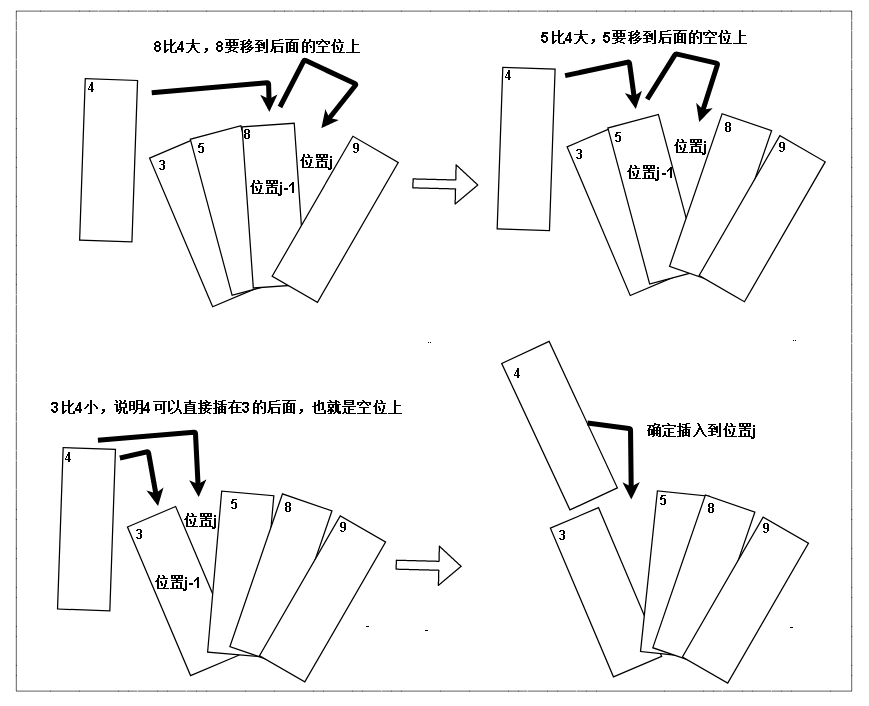
我们发现,只要抽出来的牌,不小于 j - 1 位置的牌的大小,那么他就可以插到位置 j 上,也就是空位上
同时我们发现,j 是不断往前移动的(减小),而且仔细观察一下,是较大的牌挪动到后一个位置(也就是空位 , 位置 j )之后
j 才要向前移动,因为 j 代表的是空位, 而刚刚我们把大的牌挪到后面了,所以 j 理所应当就是大牌移走之后,大牌留下的那个空位
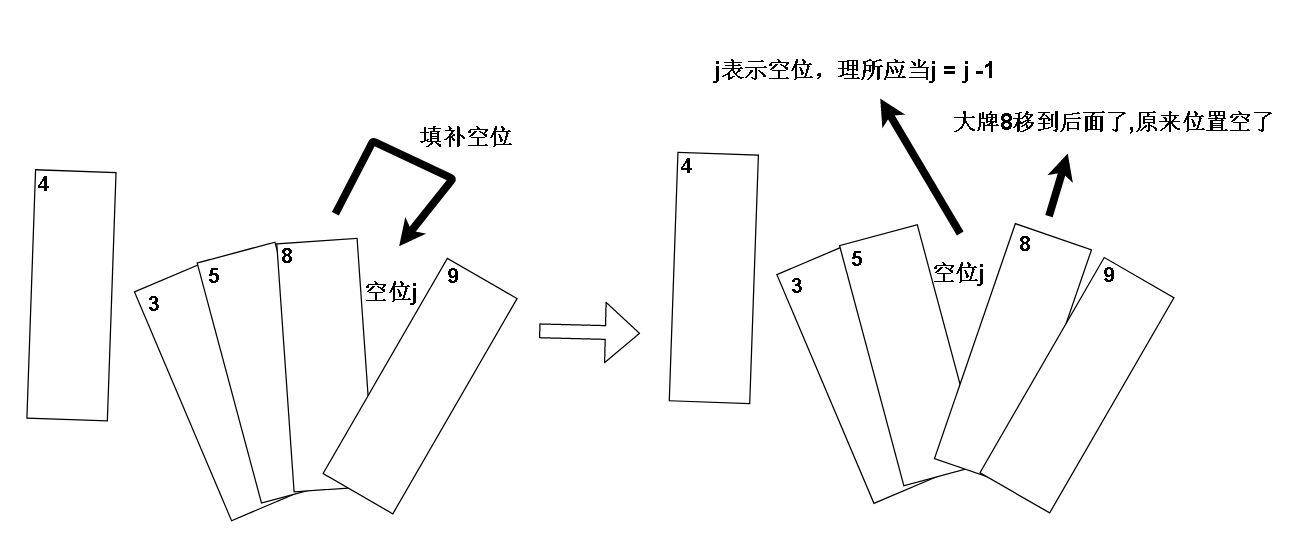
于是我们摸清楚了 4(哨兵) 是怎么插入到有序区的,表示空位位置的变量 j 是怎么变化
1. 当空位 j 之前的位置 (j - 1) 上的元素,大于哨兵的话,j - 1 位置上的元素就要继续往后挪,挪到空位 j 上
2.第1步,挪完后,空位 j 需要往前挪,也就是 j = j - 1
3.当 j - 1 的元素不大于哨兵元素,我们就要把哨兵插入到空位 j 上
按照上面的思想,我们来完善代码 :
public void insertionSort(int[] arr){ int j; for(int i = 1; i < arr.length - 1; i ++){
//触发比较 if(arr[(j = i + 1)] < arr[i]){ //设置哨兵 arr[0] = arr[j]; do { //空位的前一个元素(arr[j - 1])挪到空位(arr[j])上 //以及挪动后空位 j 往前挪, 也就是j = j - 1 arr[j] = arr[j = j - 1]; //比较空位前一个元素(arr[j - 1])和哨兵谁大 //当前一个元素大的时候,他将继续往后挪 }while(arr[j - 1] > arr[0]); //哨兵插入空位上 arr[j] = arr[0]; } } }


以上就是我们的直接插入排序,可能有人会问 j - 1 的位置会不会越界,看代码会发现 i 从 1 开始,而 j 从 i + 1开始,也就是至少 2 开始,而 j 每减一次 1 ,总是
要和 arr[0], 比较,当 j - 1 = 0,arr[ j - 1 ] > arr[0] 比不可能成立,while循环结束,所以 j - 1 不会有小于0访问数组的危险
算上有用的行,整个排序有7行,但是实际上JIT将这个排序编译成本地机器码之后的操作次数不见得比行数多几行的其他写法要少,当然也不能说一定多,因为基 本操作也就这些 : 比较,移位,插入,所用的寄存器和机器指令应该是没有多大数量的区别的。
分析一下时间复杂度 :
最坏情况下 : 所有元素逆序
假如我们有 n 个元素(不算哨兵),问题规模为n,那么我们的外层循环下标会从 1 遍历到 n - 1, 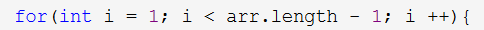
每一次都需要触发比较,并且置哨兵

第 i 趟在循环内部需要比较 i 次
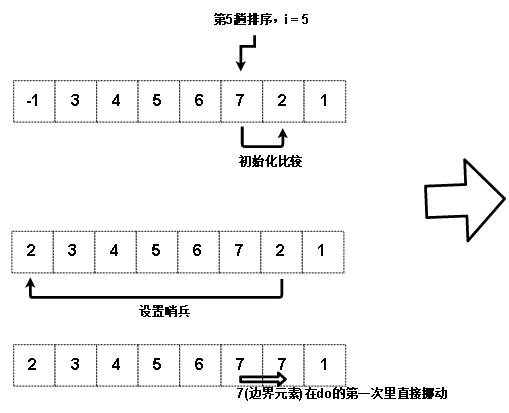
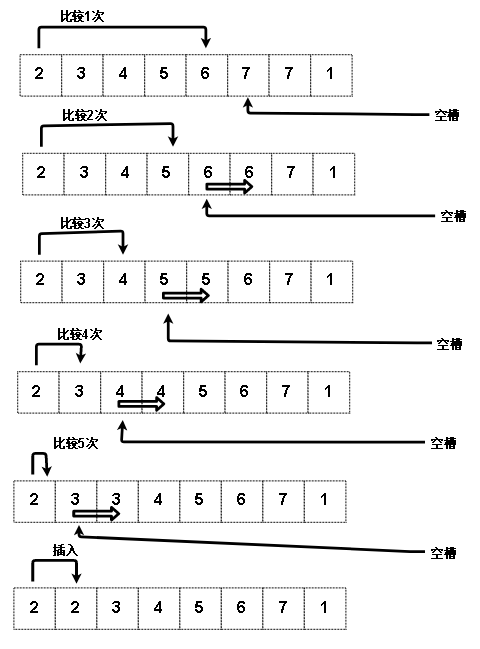
总比较次数 = 触发比较 + 内部循环比较 = i + 1
移动次数 (图中空心粗箭头)= i 次
如果把设置哨兵和最后的插入也算成移动,那么移动了 i + 2 次
Sum(1, n - 1) [( i + 1)] + Sum(1, n - 1) [( i + 2)] = [(n+2)(n - 1) + (n + 4)(n - 1)] / 2 (通过等差数列 S = n * (a1 + an) / 2得出)
如果n 无穷大,最终会趋向于 n ^ 2, 所以最坏情况下直接插入排序时间复杂度是 n^2
虽然是指数级的算法,但是他却为我们更有效的算法 : Shell (希尔)排序奠定了基础。将在下一章讲解。




