Booth算法: 补码一位乘法公式推导与解析

以下讲解内容出自《计算机组成原理(第三版)》（清华大学出版社）

大二学生一只，我的计组老师比较划水，不讲公式推导，所以最近自己研究了下Booth算法的公式推导，希望能让同样在研究Booth算法的小伙伴少花点时间。

 

 

 

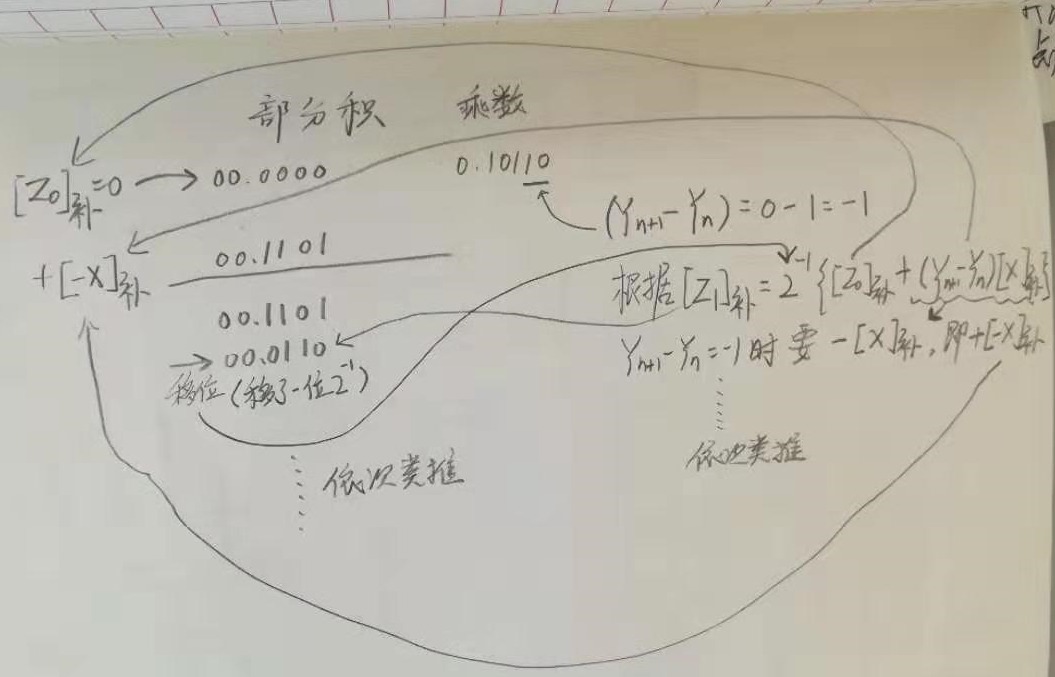
下面将对上图公式方框中部分进行讲解。

 

首先要摆明一个公式。

**公式X**： - [B]补 = [-B]补 ; [B]补 = - [-B]补

 

意思是 一个数A的补码，等于该补码的机器负数 （机器负数的定义可以见书P85 简单理解一个数Y的机器负数 = [-Y]补）

前加负号的数

比如:
 01100 (12) - [00101(5)]补 = 01100(12) + 10101(-5的补码) = (01100 + 11011)(补码) = 00111 （7的原码和补码）

 

解释1框框:
因为乘数为小数，0.ABCD = A*(2^(-1)) +  B*(2^(-2)) + C*(2^(-3)) + D*(2^(-4))。就和1111 = 1 + 2 + 4 + 8 一个道理。

 

解释2框框内容:
根据公式X， 第二行的 + [-X] 补 * Ys = - [X]补 * Ys

由此得第三行的 -Ys * [X]补

 

解释3框框中的图:
这个框中的意思是一个二进制小数，向左移动一位(乘2)，再减去原来的自己，还是等于自己。利用了二进制 高一位 是 低一位两倍的关系。
看上图中，Y1本来是表示Y1*（2^（-1））次方的大小的 ，但是在3框框中却变成了 1 * Y1（左移了一位）， 其他位以此类推。并且减去了表示原来的自己的 Y1*（2^（-1）），结果还是 Y1*（2^（-1））,所以等于原来的自己，其他位以此类推。

 

下图的Zn是部分积，并且把部分积从原式中拆解出来后，可以根据这些拆解式分析出Booth算法一位乘法补码运算时的过程

 

 

 

 

蓝色框框里的 Y(n+1) - Yn 就是乘数的末两位了(被乘数移位之后)，当 Y(n+1) - Yn  = - 1 的时候，

（Y(n+1) - Yn）* [X]补 * 2^(-n) =  (-1) * [X]补 * 2^(-n) = + [-X]补码 * 2^(-n) , X是被乘数，这也可以解释为什么Booth里末两位为10时，要加[-X]补 （因为 Y(n+1) = 0, Yn = 1）。 为什么 Y(n+1) - Yn  = 1 (末两位01)的时候 要加[X]补。而Y(n+1) - Yn  = 0 (末两位为11 或者 00)的时候什么都不做(1 - 1 = 0， 0 - 0 = 0)。而 2^(-n) 中的n则是当前部分积相对原来开始时右移的位数，所以（Y(n+1) - Yn）* [X]补 * 2^(-n) 解释起来就是 （Y(n+1) - Yn） 根据乘数末两位来确定 -1，0 , 1。也就是加还是减或者什么都不做。[X]补是原来被乘数的补码，因为乘数Y是1和0组成的，所以整个乘法X*Y的过程就是在决定要不要加X，或者不加的过程，当然补码运算比较特殊，还有减去操作。而2^(-n)的n则是表示当前乘法部分积移动的位数。

 

下图是部分积拆解结果和运算过程的对应关系分析