[全部章节]栈论 : 递归与栈式访问,如何用栈实现所有递归操作 (内附幼儿园题目,要笑着做完)
长文预警,可以先上个厕所,然后在桌子上放杯白开,静下心来看。
虽然文章长,但看完文章相信会为聪明得你带来不少收获。
重大错误说明 : 栈顶的指针始终是指向最后一个入栈元素的位置的,而不是最后一个入栈元素的位置上面!请读者留意(PS : 后来又看了一下,好像也不是什么大问题...)
1.基础知识
先回顾一下关于栈的最简单知识;
本文主要涉及线性栈
假如我们不考虑栈底,栈底是固定不动的,只考虑栈顶,那么栈就像一只放在桌子上的空杯,杯底固定贴在桌子上。
而如果我们往这个杯子里放方糖,先放进去的方糖总是被后放进去的方糖压在下面,也就是说要先取出后放进去的方糖才能取出先放进去的方糖。
这就是栈所谓的 “先进后出” 特性。
再想象一下,我们把手指压在最后放进去的方糖上面,每次取出方糖的时候用手指把方糖剔出去,之后压在下一块方糖上 。这根手指就像一个标志,标志着我们当前能剔出哪块方糖。
杯子上面还能有刻度,而且每两个刻度条之间的距离正好是一块方糖的高度。
现在把水杯,方糖和手指都抽象一下。把手指抽象成一根指向杯顶(栈顶)的指针,把方糖抽象成我们要放进去的元素(element), 把水杯抽象成一个U字型的边框,来约束我们的长方形方糖只能向上堆叠。

以下的内容都会以此数据结构作为基础,讲解递归和栈的联系
可能你写过某道题目,说要用栈来实现某某功能,不能用递归。但实际上,递归用到的数据结构本质上就是栈。所以说,递归只是在你看不到的地方用了栈,完成了你的操作。
为什么那么说呢?
我们来浅浅地了解一下在内存中函数调用的过程。
众所周知,内存是的抽象模型是一串线性的单元格。
在函数调用过程中,每个函数的开始,都会在内存中一段被称为栈区的空间内创建栈帧(稍后解释)
这片栈区 就好像我们上面说的水杯,而栈帧就是上面所说的方糖
内存被编址成一个个存储单元,上面所说的两个刻度条间的空间就可以当成一个存储单元,并且每个存储单元对应一个唯一的数字(地址)
但实际上,函数调用过程中,在内存中是用两根指针确定一个元素的,就像杯子里装了沙,你用食指和大拇指那么一捏,表示这是一个方糖高的沙。
而在函数调用中,有两个叫寄存器的东西,一个相当于大拇指,一个相当于食指,指明了两个位置,明确了一个栈帧的范围是从哪个数字到哪个数字,也就是明确了栈帧的高度和位置。
ebp 是栈底 ,esp是栈顶。 (记住 ebp 的 b = ‘base’ 基,即底的意思 )如果你没有读到这里我觉得你会读不下去。
栈帧 :
上面提到,在函数调用过程中,每个函数对应一个栈帧。那么
1.栈帧里面包含什么呢?
2.栈帧和栈帧间有什么联系呢?
3.栈帧什么时候创建和销毁呢?
以下将以简单函数调用的形式介绍

一开始,main函数没有调用add之前他的栈帧如下图,当然,下面只是简略介绍,实际上内存布局比下面更复杂(省略了寄存器等)。
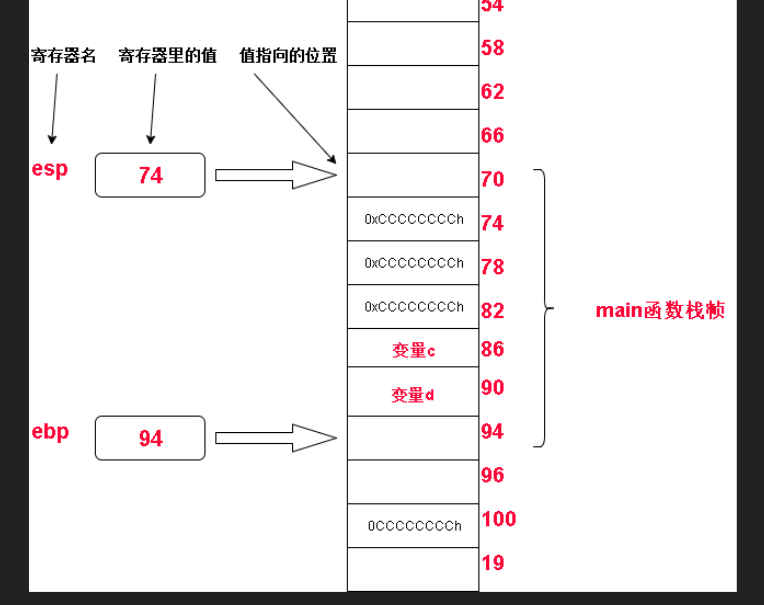
当要调用add函数的时候main 将 自己的变量拷贝后压入栈中,我们称之为“形参”
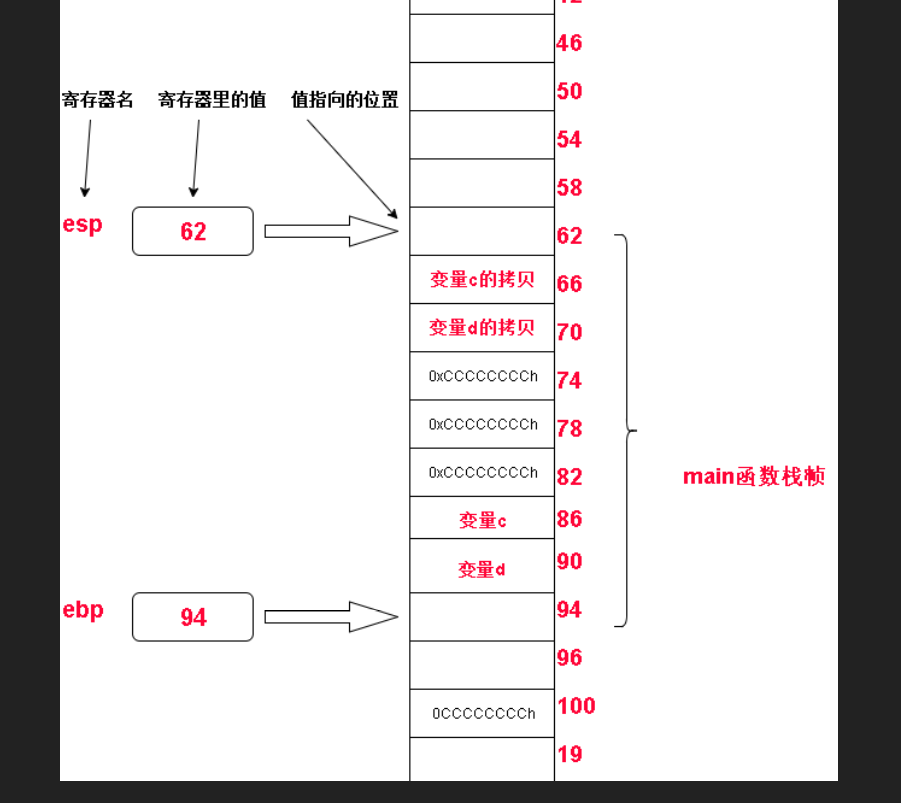
上图中变量c 和变量d的拷贝就是所谓的”形参“
接下来将main函数的ebp地址压入栈中保存,以便add函数调用完之后恢复main在内存中的栈帧

接着 就是重要的环节,add函数的栈帧创建,add函数的栈帧创建在add函数自己的操作里。
没想到吧?add函数的栈帧是add函数自己创建的。一般的思维都是父对象为子对象创建空间,再让子对象自己发挥,可能这是比较袒护孩子的行为吧,你看函数调用却是让自己的孩子去开创天地,值得学习。(当然 这是win10下汇编的得出的结果,可能不同系统不一样)
add函数本身操作 :
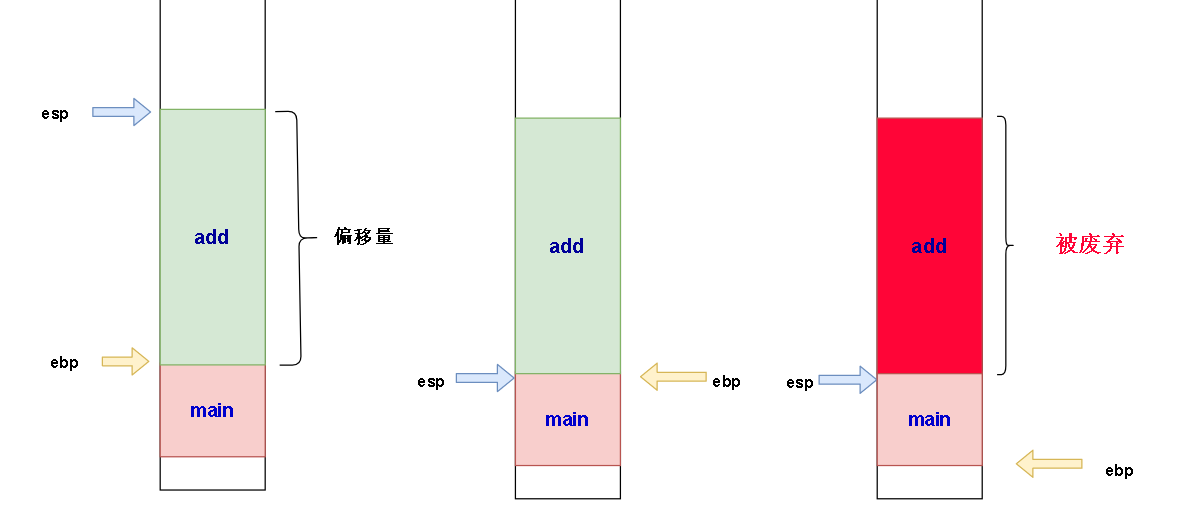
1.将esp 的值赋给ebp,这里的ebp就是add函数自己栈帧的栈底了。
2.让esp = esp - X ; X是一个位移量,表示esp要上移,esp上移的这个位移量差不多是add函数栈帧的大小。(还有一些寄存器之类的会占用空间,忽略不计)
如图:
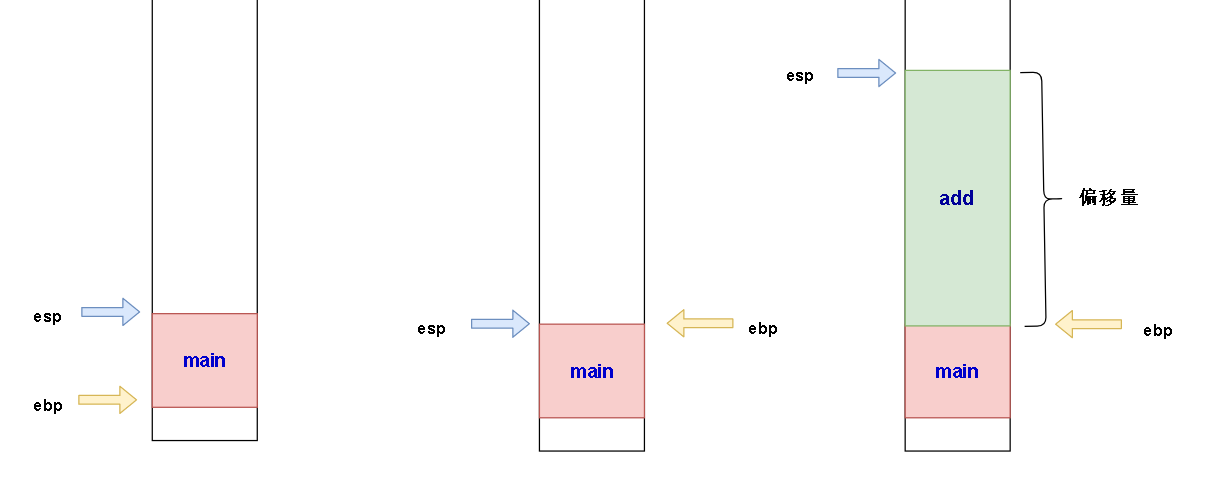
这时候的栈应该是这样的
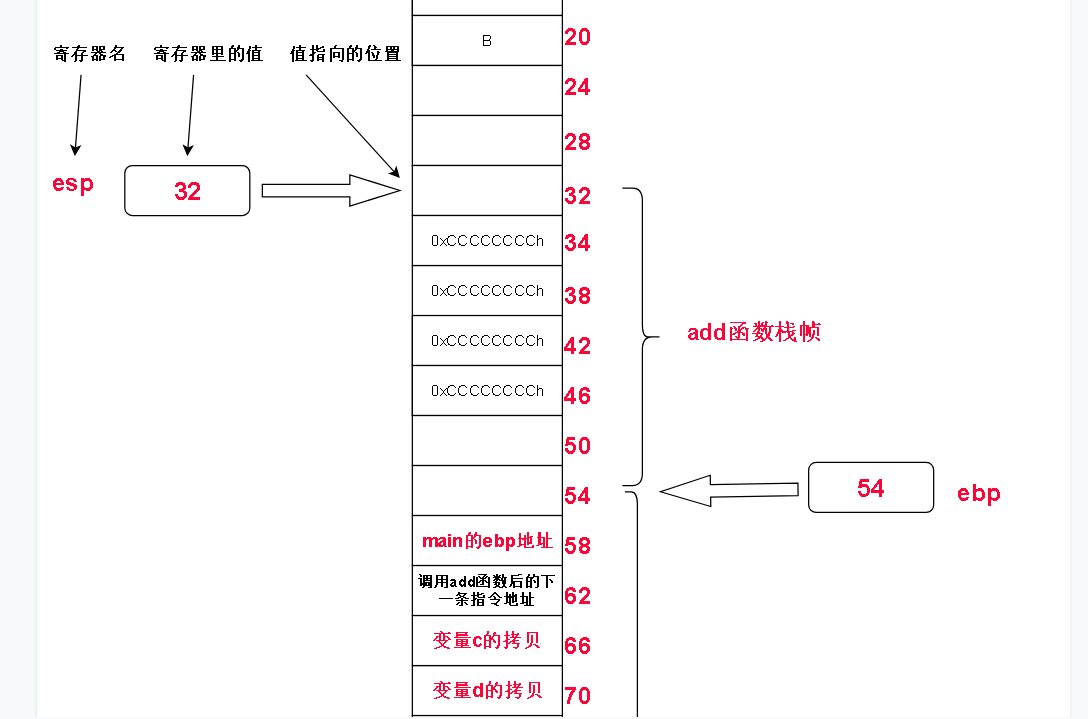
接下来,涉及到最重要环节!栈帧之间的通信
add函数的内部操作是 两个数相加,这两个数是形参,难道在add函数的栈帧中要访问在main函数栈帧中的形参吗?没错,就是直接访问。
我们来看看a + b 的汇编过程

对汇编不了解的同学可以先把 eax理解成一个变量,这个变量不在内存中(当然也就不在我们的栈区中)。mov是放进去的意思,理解把逗号右边的值放到(赋给)左边变量上(eax)去。 add是把逗号左右两边的数加起来,放到左边去。
我们发现,a + b 无非是把 ebp + 8, ebp + 12(十六进制数0Ch的十进制数)读取到的值加起来并且放到eax变量里而已。
而从 ebp + 8 和 ebp + 12 读取到的正好是main函数栈帧中的形参
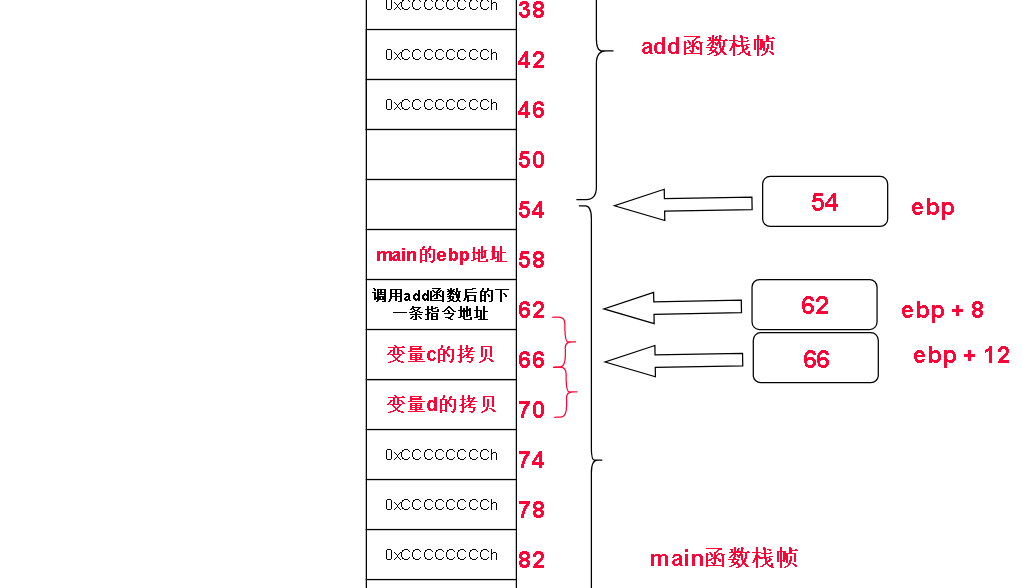
栈帧通信总结1.
子函数直接调用父函数栈帧内的形成,访问父函数
这是子向父索求信息,那么父向子索取信息呢?聪明的你可能已经猜到了,返回值!
子函数返回过程:
子函数完成之后,子函数的栈帧会被废弃掉
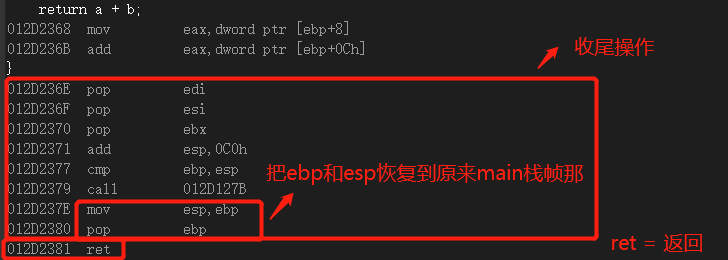
上面大圈里的小圈,两句汇编就是把栈顶和栈底移动回原来的main栈帧处。
在我们刚刚看到的a+b之后,子函数已经没什么大动作了,也就是说我们操作完之后的数是放在eax里的。
父函数就是通过访问子函数结束后遗留在eax中的数来和子函数通信,也就是说,eax里的是子函数的返回值!
从汇编也可以看到main在调用完add函数之后,为e赋值的时候直接访问了eax;

add esp,8
这句还是要好好说一说的,子函数返回之后esp还在形参的上面,既然子函数完成了,形参也没必要存在,于是需要把他们废弃掉,废弃的方法是把他们移除esp和ebp之间,也就是让esp下降就好了。
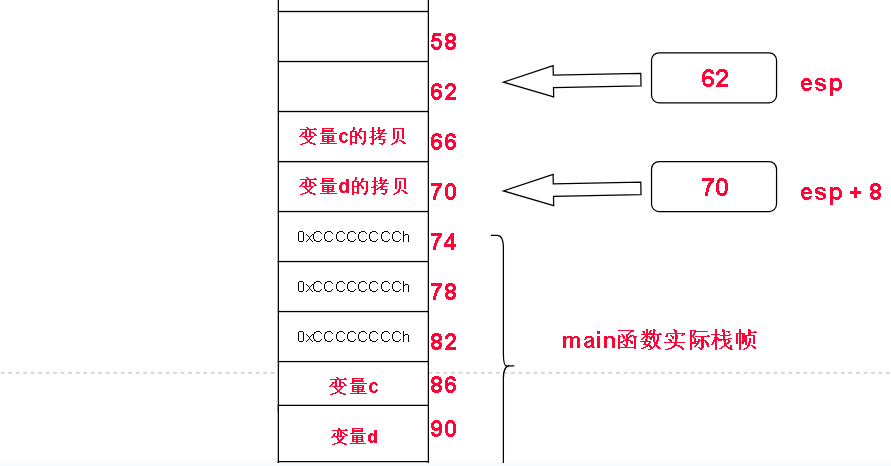
栈帧通信总结2.
父函数直接访子函数在EAX中遗留的返回值
综上,我们得出以下几点结论。
1.子函数直接调用父函数栈帧内的形成,访问父函数
2.父函数直接访子函数在EAX中遗留的返回值
3.父函数调用子函数,子函数创建栈帧,子函数完成后子函数的栈帧销毁
2.用基础知识实现递归转栈式访问
基于以上几点,我们怎么把所有的递归都用栈这个数据结构实现呢?
想必聪明的你已经有想法了吧!
例题 : (请先自己思考尝试一下怎么实现)
先给出二叉树节点定义 :
typedef struct BiTNode{
char data;
BiTNode* lchild,*rchild;
} *BiTree;
访问二叉树使用的函数 :
void visit(BiTNode * node)
如果觉得上述节点定义眼熟,那同学恭喜你,你可能是和我同一个学校的。
题1.难度等级: C
使用栈实现二叉树的先序遍历
函数头:
void preOrderRead(BiTree tree);
题2.难度等级: B
使用栈实现二叉树的后续遍历
void postOrderRead(BiTree tree);
题3.难度等级: A
二叉树的节点含有成员变量M
找出二叉树中成员变量M为a 和 b 的节点的最小祖先节点(假设a b 只出现一次)
BiTNode* findNearestAncestor(BiTree tree, char a, char b);
解析 :
题目1
首先我们需要写出大概的使用递归实现功能的代码。
题1:
void preOrderRead(BiTree tree){
if(tree == NULL){
return;
}
visit(tree);//3
preOrderRead(tree -> lchild); //1
preOrderRead(tree -> rchild);//2
}
怎么转换成栈实现呢?
从之前我们分析中知道,对函数的调用实际上是创建栈帧的过程,那么上图1,2处我们调用了两次函数,那么在这两处我们应该都要
用创建栈帧来代替。
问题是创建的栈帧里面应该包含什么内容呢?
应该包含这个栈帧创建到销毁过程中所有需要的信息。而这里的信息可能不是直接获得的,例如可能我们的栈帧中包含了一个指向父栈帧的指针,那么我们就可以和父栈帧
通信,而无需要把父栈帧中的某些变量之类的信息冗杂地包含到栈帧里来。
严谨一点地说,栈帧应该包含本栈帧创建到销毁过程中需要的所有信息的 “来源或者信息本身”。
还有更重要的一点,递归函数的方法体只有一个,也就是说,对说有的栈帧都要进行同一个操作,无论这个栈帧包含的信息有多么不一样!
所以,方法中对栈帧的处理至关重要,他将作用于所有栈帧。
要能够根据栈帧内包含的信息对信息不同的栈帧做出合理的操作。
返回我们的题目1。除去1和2这两个创建栈帧的过程。如果把当前方法的调用想成一个栈帧,那么我们在栈帧里需要执行的操作只是判断本栈帧的节点是否为空,不空就读取,仅此而已。
对应的,设计我们的函数实现.
在这里,我们把栈的元素直接设计为节点,因为节点的信息已经够我们完成所有操作(只有visit操作而已);
1.如果把栈帧的入栈想成函数调用,出栈想成函数返回,那么当栈为空的时候,函数调用就结束了。于是有了下面1处的判断栈是否是空的
2.你可能会问:子函数都没调用完,2处怎么就把父函数的栈帧出栈了呢?因为如果我们在把子函数栈帧入栈(调用子函数)前将父函数的所有操作都做了,并且子函数的栈帧不需要和父函数栈帧通信的话,那么父函数的栈帧没有存在在栈中的意义了,因为该执行的都执行完了,子函数也不需要他,子函数在栈中的顺序也不会变,好一可怜的老父亲。
在下面需要对栈帧做的所有操作只有visit,也就是访问他的节点,子函数栈帧入栈前(调用子函数)就可以把父函数的所有操作在3处完成了,没有其他操作要等待子函数栈帧出栈(返回)接着做,而且子函数的栈帧已经包含所有操作需要的信息了(BiTree),所以2处父栈帧直接出栈。
4,5两处子函数栈帧入栈,表示父函数递归调用子函数。注意要放右孩子 rchild先,因为栈是先入后访问,而且左孩子总是先于右孩子访问
void preOrderRead(BiTree tree){
Stack stack;
init(stack);
stack.push(tree);
while( ! empty(stack)){ // 1
BiTNode* node = stack.pop(); // 2
if(node == NULL){
continue;
}
visit(node); // 3
stack.push(tree -> rchild); // 4
stack.push(tree -> lchild); // 5
}
}
题目2
题目2和题目1最大的不同点是访问顺序变了。
我们对应的伪代码应该如下:
1,2,3表示的是先递归读取左子树,再是右子树,最后读取自己
void postOrderRead(BiTree tree){
if(tree == NULL){
return;
}
preOrderRead(tree -> lchild); //1
preOrderRead(tree -> rchild);//2
visit(tree);//3
}
看完上一道题的解析,应该熟能生巧了吧~
首先,我们列出每个栈帧应该具有的信息 :
1.当前节点
其次,我们理一下逻辑思路
下面的左子函数 = 左节点的子函数
首先,因为父函数中对节点的读取是在子函数退出之后的(3在1和2之后),所以父函数的栈帧在子函数栈帧入栈时不能出栈(不能退出),要等待子函数出栈,
操作完3之后才能出栈。如果我们现在我们从栈中访问了一个节点(注意是访问,不是弹出,因为父栈帧不能随意弹出),因为是后序遍历,所以要访问左子树先
也就是执行1处,所以总是要把包含左子节点的栈帧入栈。只有等到左子树是空才停止。
但是现在有一个问题,当我们访问到一个节点,我们怎么知道他的子函数栈帧该不该创建呢(子函数调用),因为此时可能是子函数调用过并退出,当前栈帧才露出来给我们获取到。另一种是子函数还没有调用,现在的栈帧是刚创建的,需要马上调用子函数。总结来说就是我们在当前节点不知是该调用子函数还是自己退出。造成这种情况的原因是,因为函数是顺序执行的,即使在同一个栈帧中,这段栈帧对应的程序是可以知道当前程序执行到的行号的。也就是说知道是否该调用子函数。而我们从栈帧得到栈帧,如果不带有类似行号的信息,根本不知道是否该调用子函数。
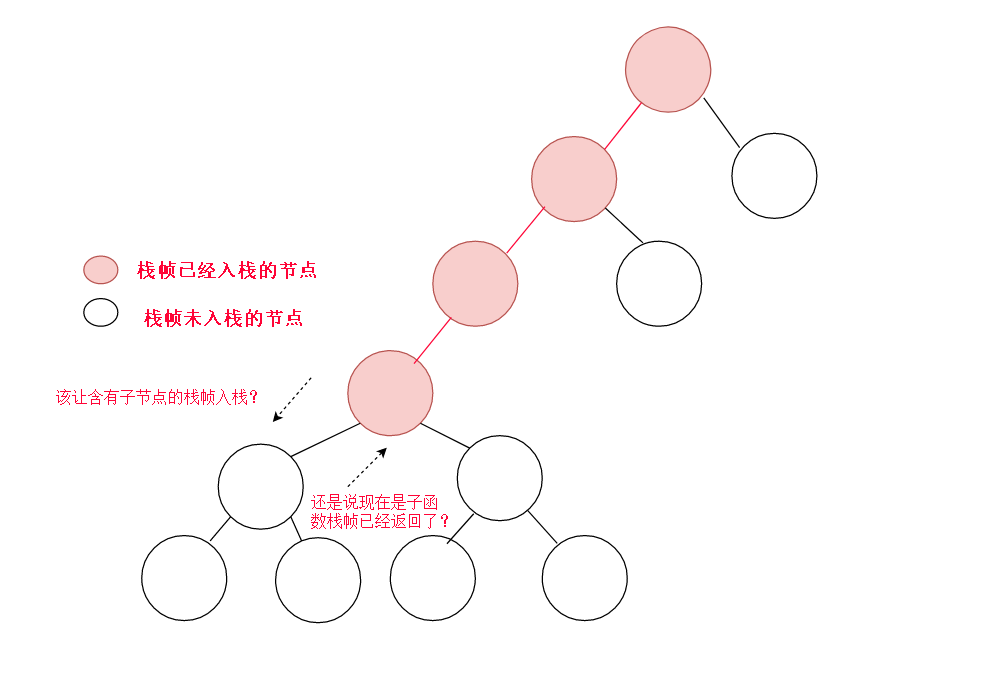
所以,栈帧里的信息,我们需要修改一下。
每个栈帧应该具有的信息 :
1.当前节点
2.当前节点是否已经调用过左/右子函数
第二点和行号有差不多的功能,但我们只需要是否调用过子函数的信息,行号太细了,可以但是没必要。
那么用什么来存储这个信息呢?
我的想法是用一个int型的变量,一个int型的变量一般是32位,也就是说他可以存储32个“是与否的信息”。
我用最低位为1表示还需要将左子函数栈帧入栈(还没调用过),为0表示已经把左子函数栈帧入栈了。
依次类推,第二位来对应右子函数。

你可能会问我这样选是否合理,我个人觉得还是相对合理的。
原因如下:
1.首先存储信息的载体体积较小,只用一个变量,充分利用每一位的信息。
2.其次是虽然每次获取信息都需要进行与掩码的操作(例如 A | (00000000 00000000 00000000 00000001) = 是否左子函数栈帧入栈),但是这样的操作耗时还是相对较少的。相比之下,如果我们用了很多个变量,频繁读取这些变量的时候,高速缓存的cache line 可能就会被提前填满,导致我们缓存的优势发挥效能降低,CPU运行速度下降。而且 | 操作在硬件层面讲是时间复杂度为O(1)的操作,因为每一位的信号都可以并行通过与门。而移位则需要等待下一位的触发器接受到上一位的触发器信息,上一位的触发器才能接受上上一位的触发器信息,存在等待问题,所以硬件层面的时间复杂度是O(n)。选与操作还是比较好的。当然,这只是从我有限的硬件知识推理分析的,如果有说错的地方请赐教。当然你也可以不运算,直接将这个int的不同值对应不同的情况,比如0表示调用左子函数,1不是不要,2表示调用右子函数,3表示不要......但是这样没有了0和1这样相反的思维逻辑条理性,而且情况一多处理麻烦。

实现代码如下 :
栈帧定义 :
typedef struct FunctionFrame {
BiTNode * node;
int tag; // 标志是应该往右走还是往左走
};
具体实现
Stack stack;
FunctionFrame frame;
int initial;
initial = 0b0011; //初始值 表示两边都还要调用
init(stack);
frame = {&node, initial};
push(stack, &frame);
while (!stackEmpty(stack)) { //栈不空表示还有函数在调用中
FunctionFrame* frame = getTop(stack); //不是弹出的访问
if (frame -> tag & 0b0001) { //如果最低位是1
if (frame ->node ->lchild != NULL) { //左孩子节点不为空
FunctionFrame* lc = (FunctionFrame*) malloc(sizeof(FunctionFrame)); //创建左子节点的函数栈帧
lc->node = frame->node->lchild;
lc->tag = initial;
push(stack, lc); // 左子函数栈帧入栈
frame->tag = frame->tag & 0b0010; //将最低位(调用左子函数的标志)抹除掉
continue; //左子函数栈帧入栈 右子函数就不要入了,因为要等待左子函数调用完右边才能调用
}
}
//如上,以此类推
if (frame ->tag & 0b0010) {
if (frame->node->rchild != NULL) {
FunctionFrame* rc = (FunctionFrame*)malloc(sizeof(FunctionFrame));
rc->node = frame->node->rchild;
rc->tag = initial;
push(stack, rc);
frame->tag = frame->tag & 0b0001;
continue;
}
}
visit(frame -> node);
pop(stack);
}
题目3
这一题,乍一看和之前题目间明显的区别是什么呢?没错,聪明的你可能已经想到了,子函数要和父函数通信了,子函数需要告诉父函数a或b在不在自己这里,自己有没有找到a或b。
如果我们把二叉树的每个节点都抽象成一个节点带着左边一大片的左子树,和右边一大片的右子树

那么我们只用分以下几种情况讨论
1.如果节点的左子树找到了a或b中的一个值,而右子树中找到另一个值,那么当前节点就是我们要找的最近祖先节点了。
2.如果其中一颗子树找到了a或b中的一个值,但是另一颗树没有找到另一个值,说明另一个值可能在另一颗子树里 ( 例: 左子树找到了a 但是右子树没找到b 说明b可能在左子树里)
3.左右子树都没找到任一一个值,说明当前节点需要被排除
4.比较特殊的情况
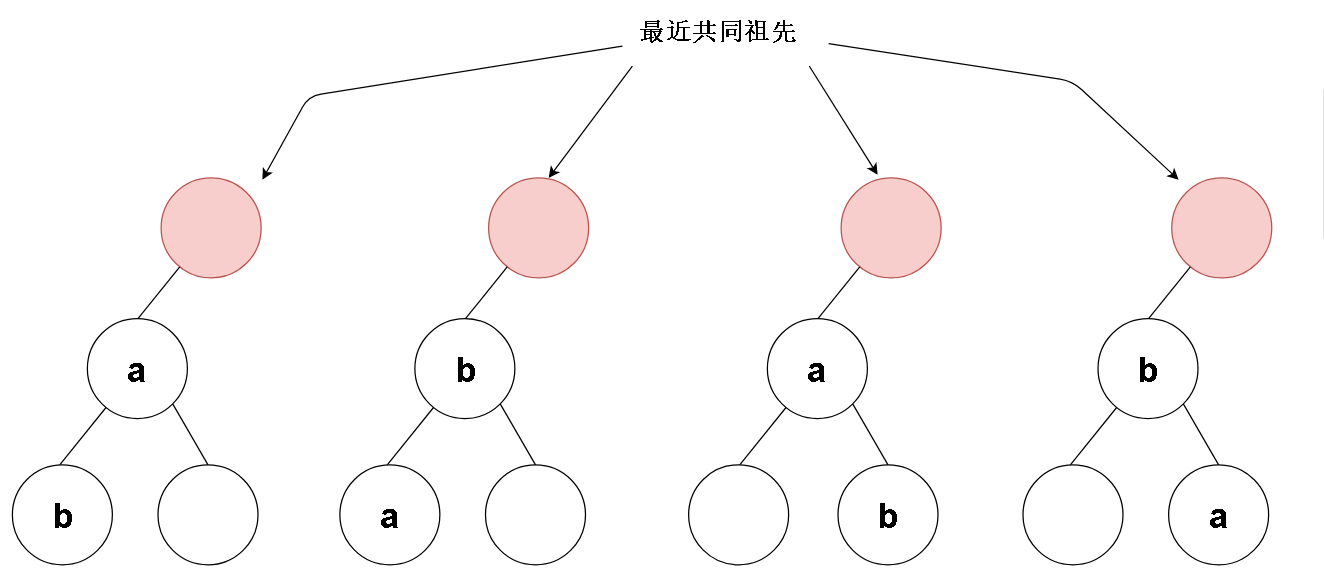
把思维反转一下,从低向上地思考,好像处了特殊情况4外其他情况都是下图这种 。有待查找值的节点最终会向中间交叉汇聚,得到我们的目标节点
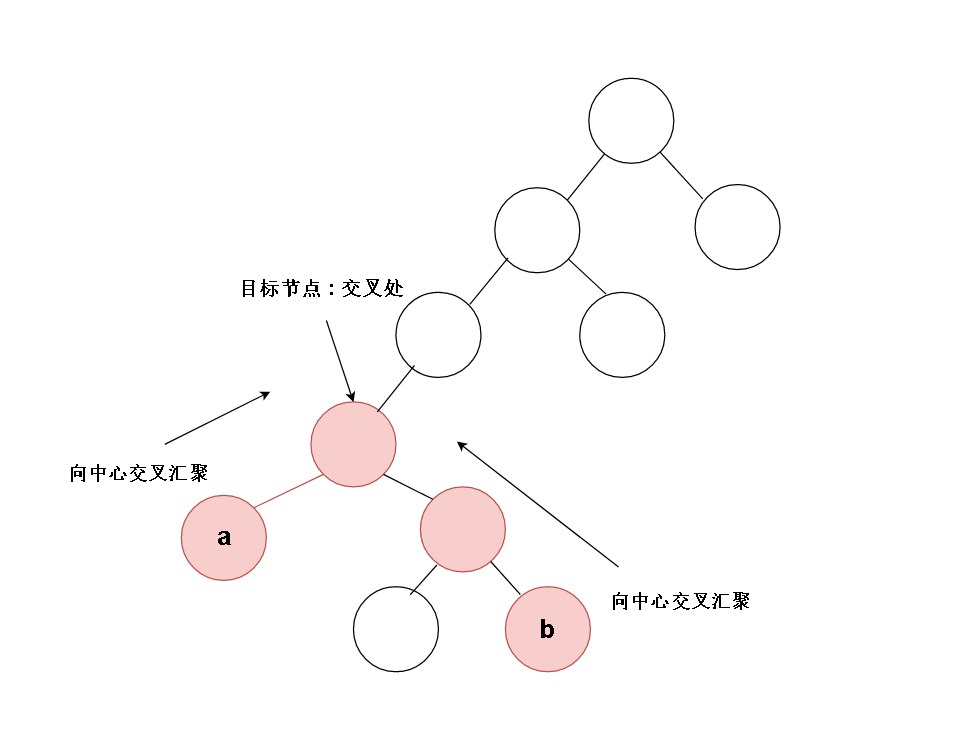
如果我们在递归中把对子函数的调用放在最前面,把对自己的处理放在最后边(正如后序遍历)。那么对二叉树的访问,总是会呈现自底向上的访问效果,而访问子节点的子函数和父函数之间是能通过返回值进行信息传递的,那么左右节点找到的信息会自底向上地交汇到我们地目标节点那,目标节点知道了一切,于是他确定自己是最近地共同祖先。
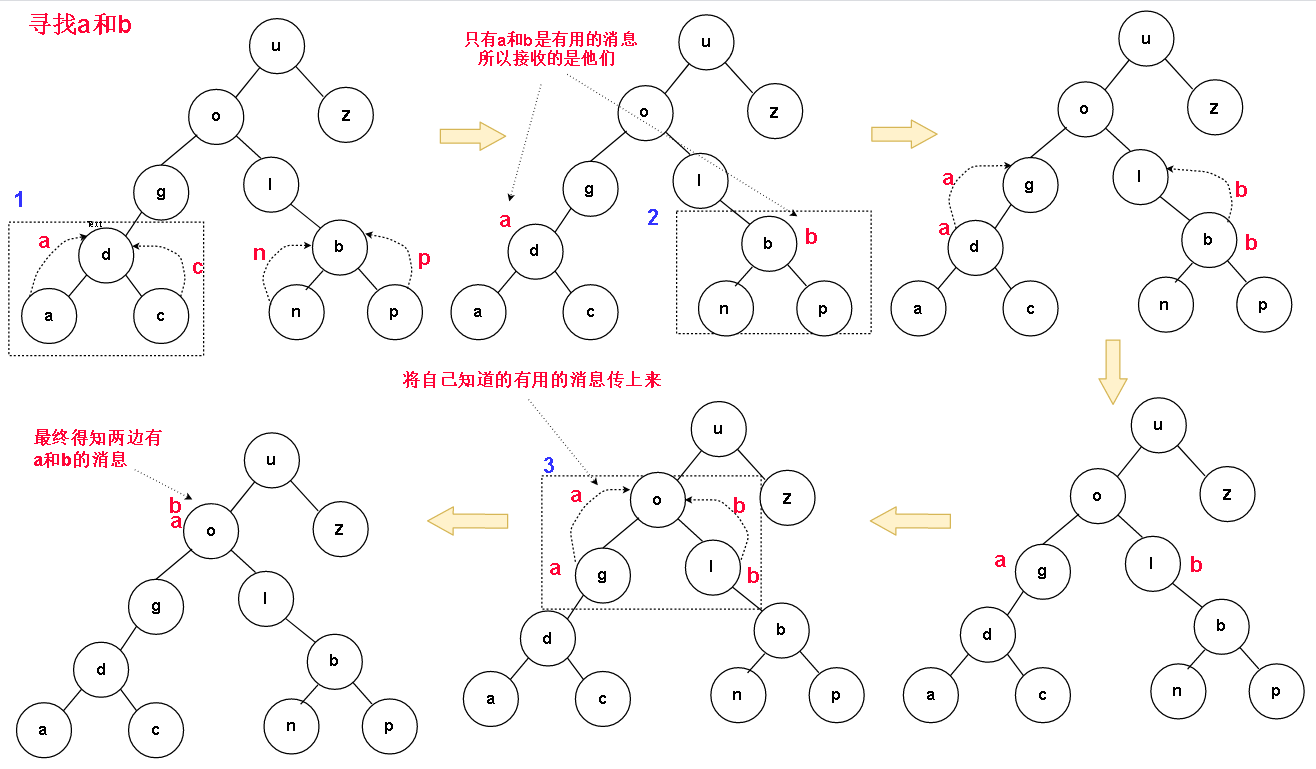
但是要时刻注意,无论是递归还是我们的栈式实现,最终只能有一套方法处理栈帧,我们的父子栈帧交流也只有一套。怎么设计这一套交流机制呢?
1.一个节点需要为他的父节点汇报消息
2.一个节点需要问他的左右孩子节点,有用的信息
节点间交流的信息应该是一个值,而且是和a,b同类型的值(char)就够了,用来告诉父节点是否找到了。
对于点1
1.节点自己的值就是一个待查找的其中一个值
查看左右两个孩子传来的值,如果其中有另一个值,那么当前节点的父节点就是我们的目标节点(对应特殊情况的配图)。如果左右孩子中不存在另一个值,那么就将自己的值传上去(上图框2中的值为p的节点)。
2.如果自己节点的值根本就不是查找的目标值:
左右孩子传来的值正好是那对我们查找的值(上图中值为o的节点),说明当前节点是我们的目标节点。而如果左右字节的传来的值中只有一个是目标值的话,就将这个值传上去给当前节点的父节点(上图框1中值为d的节点)。如果左右传来的值里没一个是要找的值,那么也不知道传什么,把自己的节点值传上去吧,反正也不是要找的值,就表示没找到。
有思路吗?如果没有的话可以先试试写下递归来实现。
char,BiTree findNearestAncestor(BiTree tree, char a, char b){
if(tree == NULL){
return -1;
}
char lv = findNearestAncestor(tree->lchild);
char rv = findNearestAncestor(tree->rchild);
if(tree -> data == a || tar -> data == b){
if(lv == a || lv == b || rv == a || rv == b){
return parent;//直接返回父节点,这里写的是伪代码,所以假设可以直接找到当前节点的父节点,实际上在递归的栈帧通信中要把父节点作为形参才能这么做。
}
return tar -> data;
}
if(lv ^ a ^ rv ^ b){ // 如果(lv,rv)是(a,b)或者(b,a) 那么 a^b^a^b = b^b^a^a = 0 , 也就是lv 和 rv 一对值和 a ,b一对值对应的时候 结果是0,所以走的是else分支 //以下是a b 不对应 lv rv 的结果 if(!((lv ^ a) & (lv ^ b))){ // lv和其中a b 其中一个相同 : ( lv ⊙ a) + (lv ⊙ b) = !!(( lv ⊙ a) + (lv ⊙ b)) = !((lv ⊕ a) * (lv ⊕ b)) return lv; } if(!((rv ^ a) & (rv ^ b))){ // rv和其中a b 其中一个相同 : ( rv ⊙ a) + (rv ⊙ b) = !!(( rv ⊙ a) + (rv ⊙ b)) = !((rv ⊕ a) * (rv ⊕ b)) return rv; } }else{ return tree; //如果左右子传来lv rv 和 a b 对应上,那么目标节点找到了 就是当前节点 } }
你可能会问,嗯???怎么会有两个返回值???是的,就是两个,记得之前我们研究方法栈帧间父子函数通信的方式么?是的,子函数在寄存器eax上遗留值,让父函数去捡,这就是一个返回过程,那么我们为什么不能安排两个寄存器呢?把两个值分别仍在两个寄存器那里,让他们成为两个返回值给父函数捡。
下面我们来安排栈帧该有的信息:
从函数调用的参数(BiTree tree, char a, char b)大概可以总结为
1.当前节点
2.待查找的a的值
3.待查找的b的值
另外还需要一个值作为方向舵,判断当前节点是否将左子函数栈帧,右子函数栈帧入栈以及当前栈帧是否弹出。
而且我们发现每个栈帧要查找的值是不变的,也就是a和b的值是不变的,所以a 和 b 可以提取出来,不作为栈帧信息,而是作为全局信息存在(类似eax寄存器)。
最重要的一点是,父函数的栈帧需要保存子函数在eax中留给自己的值,因为其他的子函数会把eax的值覆盖掉!
平时我们看到的类似如下的代码,好像是两个东西返回值值加相加,但实际上是一个返回值要先暂存起来,等另一个返回值覆盖了eax之后,再加在一起
int a = add(1, 2) + add(3, 4);
return a;

而类似我们的 char lv = findNearestAncestor(tree->lchild);
这种形式,如同下面,也是要一个变量的内存空间存储的。

我们直接把返回值存储在栈帧中,改正一下,我们的栈该有的信息:
1.当前节点
2.方向变量
3.左/右子函数返回的值
相比之前 栈帧多了成员lret,rret 分别表示左函数返回值和右函数返回值:
typedef struct FunctionFrame {
BiTNode * node;
char lret, rret; //一开始都设置为 -1,表示还没有赋值过
int tag;
};
实现代码 : 请深吸一口气,平复一下心情再看。
BiTree findNearestAncestor(BiTree tree, char a, char b) {
Stack stack;
init(stack);
FunctionFrame frame;
int initial;
int original;
initial = 0b0011; //初始值 表示两边都还要调用
original = -1;
init(stack);
frame = { tree, (char)original, (char)original, initial };
push(stack, &frame);
char ret = original; //相当于eax
while (!stackEmpty(stack)) {
FunctionFrame* frame = getTop(stack); //不能随便弹出,因为父子函数栈帧之间需要进行通信
if (frame->tag & 0b0001) { //如果最低位是1
if (frame->node->lchild != NULL) { //左孩子节点不为空
FunctionFrame* lc = (FunctionFrame*)malloc(sizeof(FunctionFrame)); //创建左子节点的函数栈帧
lc->node = frame->node->lchild;
lc->tag = initial;
lc->lret = lc->rret = original; //一开始都设置为 -1,表示还没有赋值过
push(stack, lc); // 左子函数栈帧入栈
frame->tag = frame->tag & 0b0010; //将最低位(调用左子函数的标志)抹除掉
continue; //左子函数栈帧入栈 右子函数就不要入了,因为要等待左子函数调用完右边才能调用
}
}
//因为有调用左边的continue阻挡,所以到了这里表示已经从左子函数返回了
if (frame->lret == original) {
frame->lret = ret; // 这时候就该把左子函数返回的值保存起来
}
//右边情况和上边的左边类似
if (frame->tag & 0b0010) {
if (frame->node->rchild != NULL) {
FunctionFrame* rc = (FunctionFrame*)malloc(sizeof(FunctionFrame));
rc->node = frame->node->rchild;
rc->tag = initial;
rc->lret = rc->rret = original;
push(stack, rc);
frame->tag = frame->tag & 0b0001;
continue;
}
}
if (frame->rret == original) { //其实也可以不用加 rret这个变量的,因为到了这一步直接用右子函数返回的值就可以了,不用保存
frame->rret = ret;
}
char mine = frame->node->data;
char lv = frame->lret;
char rv = frame->rret;
if (lv ^ a ^ rv ^ b) { //如果(lv,rv)和(a,b)或者(b,a)不相同
if (!((lv ^ a) & (lv ^ b))) { //lv和a或b之中一个相同 当前节点返回lv
ret = lv;
}
if (!((rv ^ a) & (rv ^ b))) { //rv和a或b之中一个相同 当前节点返回rv
ret = rv;
}
if (mine == a || mine == b) { //如果当前节点的值是要查找值中的一个
if (lv == a || lv == b || rv == a || rv == b) { //如果左边或者右边传来的值是要找的另一个
pop(stack); //当前节点直接出栈 直接去找他的父节点
if (stackEmpty(stack)) { //如果栈是空的 表示根节点的值是我们要查找的值,根节点无祖先,返回空
return NULL;
}
else {
return pop(stack)->node; //直接返回当前节点的双亲节点
}
}
ret = mine; // 如果左右传来的值中没有要找的,那么就返回自己的值
}
}
else {
return frame->node; // 左右传来的值正好都是要查找的值 当前节点就是目标节点
}
pop(stack); // 调用完成后出栈
}
return NULL; // 栈空了都没找到,表示两个节点不全在树种
}
从题目可以看到。
1.我们的栈实现方式,可以以局部变量模拟寄存器的形式,在逻辑上返回多个返回值
相当于我们有这样的函数:
char,int,bool get(){ //相当于有了return + 返回编号 这样的形式
return1 'c'; //作为第1种返回类型返回
return2 3; //作为第2种返回类型返回
return3 false; //作为第3种返回类型返回
}
2.另外,一般栈的大小是小于堆的,我们把栈帧的开辟转移到了堆上,可能访问速度有所下降,但对于处理数据大的函数,可能可以防止栈溢出,但不能防止堆溢出。
3.可以让子函数强行和父函数通信,获得父函数的某些信息,如上面直接就把父函数栈帧出栈并且返回父函数栈帧里的节点了。
4.减少栈帧中的变量,如果这些变量在递归函数的调用中作为形参时不会变,或者变得很少。
当然缺点也不少:
1.代码复杂,烧脑
2.如果栈是建立在堆上的话,访问速度会下降
3.我们是用软件来模拟硬件层次的操作,所以效率多多少少会下降
更多幼儿园题目还在上线中......
护眼绿:
没人看的结语:
首先很感谢你看到这里,辛苦了。
文章中某些地方可能不正确或不准确,代码也可能不够高效可读,希望读者能够帮忙指正,共同学习进步。
(PS : 后来又看了一下,好像也不是什么大问题...)



