图

图

　　图是一种用顶点和边来表示关系的数据模型，一般用来表示多对多关系。图分为无向图和有向图两种。例如：

　　

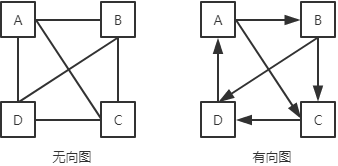
　　无向图中“A — B”表示A可以直接到达B，B也可以直接到达A；有向图中“A —> B”表示A可以直接到达B，而B不能直接到达A。即无向图的边是双向可达的，有向图的边是单向可达的。

图的表示

　　图可以用一个二维数组表示，其中0表示不能直接到达，1表示可以直接到达。例如：

　　

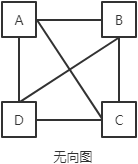
　　可以表示为：

	A	B	C	D
A	0	1	1	1
B	1	0	1	1
C	1	1	0	1
D	1	1	1	0

　　 

　　可以表示为：

	A	B	C	D
A	0	1	1	0
B	0	0	1	1
C	0	0	0	1
D	1	0	0	0

---

　　图还可以用一个链表数组表示，链表中的元素为该顶点可以直接到达的顶点。例如：

　　

　　可以表示为：

A	B -> C -> D
B	A -> C -> D
C	A -> B -> D
D	A -> B -> C

　　 

　　可以表示为：

A	B -> C
B	C -> D
C	D
D	A

　　用链表表示图的代码如下：

public class Graph {

    private ArrayList<String> vertices;
    private ArrayList<LinkedList<String>> edges;

    public Graph() {
        vertices = new ArrayList<String>();
        edges = new ArrayList<LinkedList<String>>();
    }

    public void addVertices(String ... vertices) {
        for (String vertice : vertices) {
            this.vertices.add(vertice);
            edges.add(new LinkedList<String>());
        }
    }

    public boolean addEdge(String from, String to, boolean isDirected) {
        if (! vertices.contains(from)) {
            System.err.println("起点不存在！");
            return false;
        }
        if (! vertices.contains(to)) {
            System.err.println("终点不存在！");
            return false;
        }
        edges.get(vertices.indexOf(from)).add(to);
        if (! isDirected) edges.get(vertices.indexOf(to)).add(from);
        return true;
    }

    @Override
    public String toString() {
        String str = "";
        for (int i = 0; i < vertices.size(); i++) {
            str += vertices.get(i) + ": ";
            for (String edge : edges.get(i)) {
                str += edge + " ";
            }
            str += "\n";
        }
        return str;
    }

}

　　其中，vertices表示顶点，edges表示边。

图的遍历

　　图有两种遍历方式：深度优先遍历（Depth First Search，DFS）和广度优先遍历（Broad First Search，BFS）。

　　深度优先遍历的步骤如下：

　　a. 判断当前顶点是否遍历，如果没有则遍历当前顶点。

　　b. 若当前顶点有可以到达的顶点，则按顺序递归遍历所有可以到达的顶点。

　　c. 若还有没有遍历的顶点，则返回步骤a，直到遍历完所有结点。

　　深度优先遍历的代码如下：

public void dfs() {
    System.out.print("深度优先遍历：");
    boolean[] isVisited = new boolean[vertices.size()];
    for (int i = 0; i < vertices.size(); i++) dfs(i, isVisited);
    System.out.println();
}

private void dfs(int start, boolean[] isVisited) {
    if (isVisited[start]) return;
    System.out.print(vertices.get(start) + " ");
    isVisited[start] = true;
    for (String edge : edges.get(start)) dfs(vertices.indexOf(edge), isVisited);
}

　　例如，从顶点A开始进行深度优先遍历：

　　

　　a. 遍历顶点A，顶点A有可到达的顶点B和C。

　　b. 遍历顶点B，顶点B有可到达的顶点C和D。

　　c. 遍历顶点C，顶点C有可到达的顶点D。

　　d. 遍历顶点D。

　　输出结果为：

　　

---

　　广度优先遍历的步骤如下：

　　a. 判断当前顶点是否遍历，如果没有则遍历当前顶点。

　　b. 若当前顶点有可到达的顶点，则按顺序遍历所有可到达的顶点。

　　c. 按顺序判断当前顶点可到达的顶点是否有可到达的顶点，如果有则返回步骤b。

　　d. 若还有没有遍历的顶点，则返回步骤a，直到遍历完所有结点。

　　广度优先遍历的代码如下：

public void bfs() {
    System.out.print("广度优先遍历：");
    boolean[] isVisited = new boolean[vertices.size()];
    Queue<Integer> q = new LinkedList<Integer>();
    for (int i = 0, index; i < vertices.size(); i++) {
        if (! isVisited[i]) {
            q.add(i);
            while (! q.isEmpty()) {
                index = q.poll();
                System.out.print(vertices.get(index) + " ");
                isVisited[index] = true;
                for (String edge : edges.get(index)) {
                    index = vertices.indexOf(edge);
                    if (! isVisited[index] && ! q.contains(index)) q.add(index);
                }
            }
        }
    }
    System.out.println();
}

　　例如，从顶点A开始遍历：

　　

　　a. 遍历顶点A。

　　b. 顶点A有可到达的顶点B和C，遍历顶点B和C。

　　c. 顶点B有可到达的顶点C和D，顶点C已经遍历过，直接遍历顶点D。

　　输出结果为：