链表
链表
链表是采用链式结构存储的线性表。链表中的元素在存储空间中的位置不一定是连续的,所以链表使用结点来存储元素,每个节点中还存储了相邻节点位置信息。由于不是连续存储,存取元素的速度比顺序表差。但是只要存储空间足够,链表就可以动态增加长度,也就是说,相较于顺序表,链表能更快速地进行元素的插入和删除操作。
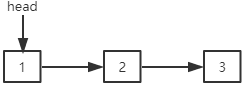
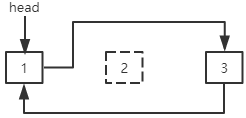
链表需要一个头指针head来表示链表的第一个结点。根据结点中存储的相邻结点信息的不同,链表又可以细分为单向链表和双向链表。若链表的第一个结点和最后一个结点相连,则该链表又可以称为循环链表。
单向链表
单向链表的结点中只保存了直接后继结点的位置信息。也就是说,每一个结点中都有一个next指针指向该结点的直接后继结点,若该结点是最后一个结点,则next取null。
单向链表的结点结构定义如下:

1 public class LNode<E> { 2 3 public E data; 4 5 public LNode<E> next; 6 7 public LNode(E data) { 8 this.data = data; 9 } 10 11 }
查找
单向链表通过遍历来找到指定位标的结点:从head指向的结点(第一个结点)开始遍历,遍历到next取值为null的结点(最后一个结点)时结束。

1 public LNode<E> getNode(int index) { 2 if (index < 0) throw new ListException("位标不能为负!"); 3 if (isEmpty()) throw new ListException("链表为空!"); 4 // 从head指针指向的结点开始 5 LNode<E> node = head; 6 // index == 0表示当前结点为待查询结点,node.next == null表示当前结点为最后一个结点 7 while (index > 0 && node.next != null) { 8 node = node.next; 9 index--; 10 } 11 return node; 12 }
可以根据指定元素来查找结点是否存在。

1 public LNode<E> getNodeByElem(E e) { 2 if (isEmpty()) throw new ListException("链表为空!"); 3 // 从head指针指向的结点开始 4 LNode<E> node = head; 5 // node == null表示查找不到指定的结点 6 while (node != null) { 7 if (e.equals(node.data)) break; 8 node = node.next; 9 } 10 return node; 11 }
插入
单向链表的插入分为三种情况:
在前面插入结点:插入结点的next指针指向第一个结点,head指针指向插入结点。

在后面插入结点:最后一个结点的next指针指向插入结点。

在中间插入结点:指定位置的前一个结点的next指针指向插入结点,插入结点的next指针指向指定位置的结点。


1 public void add(int index, E data) { 2 LNode<E> node = new LNode<E>(data); 3 // head == null表示链表为空,index == 0表示在前面插入结点 4 if (head == null || index == 0) { 5 node.next = head; 6 head = node; 7 } else { 8 // 获取指定位置的前一个结点 9 LNode<E> n = getNode(index - 1); 10 // n.next == null表示在后面插入结点,n.next != null表示在中间插入结点 11 node.next = n.next; 12 n.next = node; 13 } 14 }
删除
单向链表的删除也分为三种情况:
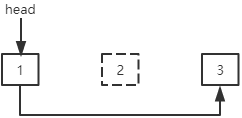
删除第一个结点:head指针指向下一个结点。
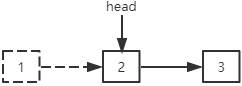
删除最后一个结点:倒数第二个结点的next指针置为null。
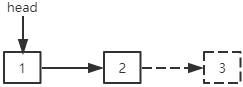
删除中间的结点:指定结点前一个结点的next指针指向指定结点下一个结点。

1 public E remove(int index) { 2 // head != null表示链表不为空 3 if (head != null) { 4 E e; 5 // index == 0表示删除第一个结点 6 if (index == 0) { 7 e = head.data; 8 head = head.next; 9 } else { 10 LNode<E> node = head; 11 // index == 1表示当前结点是指定结点的前一个结点,node.next.next == null表示当前结点是倒数第二个结点 12 while (index > 1 && node.next.next != null) { 13 node = node.next; 14 index--; 15 } 16 e = node.next.data; 17 node.next = node.next.next; 18 } 19 return e; 20 } 21 return null; 22 }
反转
实现单向链表的反转可以通过将第一个结点与之后的结点断开,之后每一个结点在前面插入,最后head指针指向最后一个结点。

1 public void reverse() { 2 // head == null表示链表为空,head.next == null表示链表中只有一个结点 3 if (head != null && head.next != null) { 4 LNode<E> node = head.next; 5 head.next = null; 6 while (node != null) { 7 LNode<E> n = node.next; 8 // 在前面插入当前结点 9 node.next = head; 10 head = node; 11 // 走向下一个结点 12 node = n; 13 } 14 } 15 }
单向循环链表
单向循环链表是第一个结点和最后一个结点相连的单向链表。单向循环链表最后一个结点的next指针指向第一个结点。
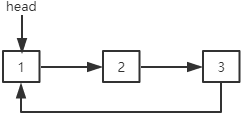
在单向循环链表中可以添加一个size变量来存储结点个数。
查找
单向循环链表可以通过循环查找指定位标的结点。指定位标可以通过对size求模来减少循环次数。

1 public LNode<E> getNode(int index) { 2 if (index < 0) throw new ListException("位标不能为负!"); 3 if (isEmpty()) throw new ListException("链表为空!"); 4 index %= size; 5 LNode<E> node = head; 6 while (index > 0) { 7 node = node.next; 8 index--; 9 } 10 return node; 11 }
可以通过指定元素来查找结点是否存在。

1 public LNode<E> getNodeByElem(E e) { 2 if (isEmpty()) throw new ListException("链表为空!"); 3 LNode<E> node = head; 4 do { 5 if (e.equals(node.data)) return node; 6 node = node.next; 7 } while (node != head); // node == head表示node已经走完一圈 8 return null; 9 }
插入
单向循环链表的插入分为两种:
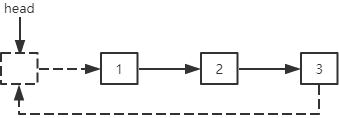
在前面插入结点:插入结点的next指针指向第一个结点,最后一个结点的next指针指向插入结点,head指针指向插入结点。
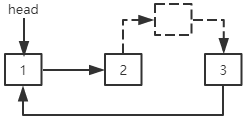
在中间插入结点:插入结点的next指针指向指定位置的结点,指定位置的前一个结点的next指针指向插入结点。

1 public void add(int index, E data) { 2 if (index < 0) throw new ListException("位标不能为负!"); 3 LNode<E> node = new LNode<E>(data); 4 if (isEmpty()) { 5 // 链表为空表,则创建一个自成环形的结点 6 node.next = node; 7 head = node; 8 } else { 9 // 对size求模减少循环次数 10 index %= size; 11 LNode<E> n; 12 if (index == 0) { 13 // 在前面插入结点,获取的是最后一个结点 14 n = getNode(size - 1); 15 head = node; 16 } else { 17 // 在中间插入结点,获取的是前一个结点 18 n = getNode(index - 1); 19 } 20 node.next = n.next; 21 n.next = node; 22 } 23 size++; 24 }
删除
单向循环链表的删除也分为两种:
删除第一个结点:最后一个结点的next指针指向第二个结点,head指针指向下一个结点。
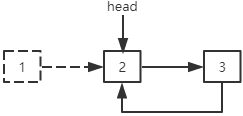
删除其他结点:指定结点前一个结点的next指针指向指定结点下一个结点。

1 public E remove(int index) { 2 if (index < 0) throw new ListException("位标不能为负!"); 3 if (isEmpty()) return null; 4 E e = null; 5 if (size == 1) { 6 e = head.data; 7 head = null; 8 } else { 9 index %= size; 10 LNode<E> node; 11 if (index == 0) { 12 // 获取最后一个结点 13 node = getNode(size - 1); 14 head = head.next; 15 } else { 16 // 获取前一个结点 17 node = getNode(index - 1); 18 } 19 e = node.next.data; 20 node.next = node.next.next; 21 } 22 size--; 23 return e; 24 }
反转
单向循环链表的反转与单向链表类似,不过需要先定义一个辅助结点保存反转后的最后一个结点,最后一步需要让最后一个结点的next指针指向反转后的第一个结点(head指针指向的结点)。

1 public void reverse() { 2 // size == 0表示链表为空,size == 1表示链表只有一个结点 3 if (size <= 1) return; 4 // 反转后的最后一个结点为现在的第一个结点 5 LNode<E> tail = head; 6 // 从第二个结点开始遍历 7 LNode<E> node = head.next; 8 while (node != tail) { 9 LNode<E> n = node.next; 10 // 在前面插入结点 11 node.next = head; 12 head = node; 13 // 走向下一个结点 14 node = n; 15 } 16 // 最后一个结点的next指针指向第一个结点 17 tail.next = head; 18 }
双向链表
双向链表的结点中保存了直接前驱结点和直接后继结点的位置信息。也就是说,每一个结点中都有一个next指针指向直接后继结点,一个prior指针指向直接前驱结点。

双向链表的结点结构定义如下:

1 public class DuLNode<E> { 2 3 public E data; 4 5 public DuLNode<E> prior; 6 7 public DuLNode<E> next; 8 9 public DuLNode(E data) { 10 this.data = data; 11 } 12 13 }
查找
双向链表也是通过遍历找到指定位标的结点。

1 public DuLNode<E> getNode(int index) { 2 if (index < 0) throw new ListException("位标不能为负!"); 3 if (isEmpty()) throw new ListException("双向链表为空!"); 4 DuLNode<E> node = head; 5 while (index > 0 && node.next != null) { 6 node = node.next; 7 index--; 8 } 9 return node; 10 }
可以通过指定元素来查找结点是否存在。

1 public DuLNode<E> getNodeByElem(E e) { 2 if (isEmpty()) throw new ListException("双向链表为空!"); 3 DuLNode<E> node = head; 4 while (node != null) { 5 if (e.equals(node.data)) return node; 6 node = node.next; 7 } 8 return null; 9 }
插入
双向链表的插入与单向链表一样,只不过在插入结点时除了设置next指针外,还要设置prior指针。

1 public void add(int index, E data) { 2 DuLNode<E> node = new DuLNode<E>(data); 3 if (index < 0) throw new ListException("位标不能为负!"); 4 if (head == null) { 5 head = node; 6 } else { 7 // index == 0表示在前面插入结点 8 if (index == 0) { 9 node.next = head; 10 head.prior = node; 11 head = node; 12 } else { 13 DuLNode<E> n = getNode(index - 1); 14 node.next = n.next; 15 // n.next == null表示在后面插入结点,n.next != null表示在中间插入结点 16 if (n.next != null) n.next.prior = node; 17 n.next = node; 18 node.prior = n; 19 } 20 } 21 }
删除
双向链表的删除也是在单向链表的基础上多一步对prior指针的设置。

1 public E remove(int index) { 2 if (isEmpty()) return null; 3 E e = null; 4 if (head.next == null) { 5 e = head.data; 6 head = null; 7 } else { 8 if (index == 0) { 9 e = head.data; 10 head.next.prior = null; 11 head = head.next; 12 } else { 13 DuLNode<E> node = getNode(index - 1); 14 if (node.next != null) { 15 node = node.next; 16 e = node.data; 17 node.next.prior = node.prior; 18 node.prior.next = node.next; 19 } 20 } 21 } 22 return e; 23 }
双向循环链表
双向循环链表是第一个结点和最后一个结点相连的双向链表。双向循环链表最后一个结点的next指针指向第一个结点,第一个结点的prior指针指向最后一个结点。
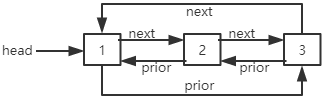
在双向循环链表中可以添加一个size变量来存储结点个数。
查找
双向循环链表可以通过循环查找指定位标的结点。指定位标可以通过对size求模来减少循环次数。

1 public DuLNode<E> getNode(int index) { 2 if (index < 0) throw new ListException("位标不能为负!"); 3 if (isEmpty()) throw new ListException("链表为空!"); 4 index %= size; 5 DuLNode<E> node = head; 6 while (index > 0) { 7 node = node.next; 8 index--; 9 } 10 return node; 11 }
可以通过指定元素来查找结点是否存在。

1 public DuLNode<E> getNodeByElem(E e) { 2 if (isEmpty()) throw new ListException("链表为空!"); 3 DuLNode<E> node = head; 4 do { 5 if (e.equals(node.data)) return node; 6 node = node.next; 7 } while (node != head); 8 return null; 9 }
插入
双向循环链表的插入是在单向循环链表的基础上多一步对prior指针的设置。

1 public void add(int index, E data) { 2 DuLNode<E> node = new DuLNode<E>(data); 3 if (head == null) { 4 node.prior = node.next = node; 5 head = node; 6 } else { 7 index %= size; 8 if (index == 0) { 9 node.prior = head.prior; 10 node.next = head; 11 head.prior.next = node; 12 head.prior = node; 13 head = node; 14 } else { 15 DuLNode<E> n = getNode(index - 1); 16 node.prior = n; 17 node.next = n.next; 18 n.next.prior = node; 19 n.next = node; 20 } 21 } 22 size++; 23 }
删除
双向循环链表的删除是在单向循环链表的基础上多一步对prior指针的设置。

1 public E remove(int index) { 2 if (index < 0) throw new ListException("位标不能为负!"); 3 if (isEmpty()) return null; 4 E e = null; 5 if (size == 1) { 6 e = head.data; 7 head = null; 8 } else { 9 index %= size; 10 if (index == 0) { 11 e = head.data; 12 head.next.prior = head.prior; 13 head.prior.next = head.next; 14 head = head.next; 15 } else { 16 DuLNode<E> node = getNode(index); 17 e = node.data; 18 node.next.prior = node.prior; 19 node.prior.next = node.next; 20 } 21 } 22 size--; 23 return e; 24 }
约瑟夫问题
据说著名犹太历史学家约瑟夫有过这样一个故事:在罗马人占领乔塔帕特后,39个犹太人与约瑟夫及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式:41个人排成一个圆圈,由第1个人开始报数,每报到3的人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而约瑟夫和他的朋友并不想遵从,于是约瑟夫要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,最终逃过了这场死亡游戏。
这个故事演化来的问题就是著名的约瑟夫问题:由n个人围成一个圈,从1开始报数,报到m的人就出圈,由下一个人继续从1开始报数......求出出圈的人的顺序。
例如编号分别为1~5的5个小朋友围成一个圈,从1号小朋友开始报数,每次报到2的小朋友出圈:
a. 1号报1,2号报2,所以2号出圈。此时圈内剩下1-3-4-5。
b. 3号报1,4号报2,所以4号出圈。此时圈内剩下1-3-5。
c. 5号报1,1号报2,所以1号出圈。此时圈内剩下3-5。
d. 3号报1,5号报2,所以5号出圈。此时圈内剩下3。
综上所述,出圈的顺序为2-4-1-5-3。
解决方案
约瑟夫问题的特点是:
1. 所有人围成一个圈。也就是说,最后一个人的下一个人是第一个人。所以,可以使用单向环形链表来表示。
2. 从当前的人开始报数,报到m的人出圈。也就是说,出圈的人是当前的人之后的第m - 1个人。所以,如果假设当前人的编号为i,那么下一个出圈的人就是(i + m - 1) % size(i + m - 1可能大于size,所以需要通过对size求模),即删除(i + m - 1) % size结点。
所以,求解约瑟夫问题方法的定义如下:

1 /** 2 * 求解约瑟夫问题 3 * @param m 报到m的出圈 4 * @return 按出圈的顺序排列的数组 5 */ 6 @SuppressWarnings("unchecked") 7 public static <E> E[] josephus(E[] datas, int m) { 8 if (datas == null || datas.length == 0) throw new ListException("没有数据!"); 9 E[] result = (E[]) Array.newInstance(datas[0].getClass(), datas.length); 10 CirLinkedList<E> l = new CirLinkedList<E>(); 11 l.addAll(datas); 12 int i = 0; // 从第一个人开始报数 13 int j = 0; 14 while (! l.isEmpty()) { 15 i = (i + m - 1) % l.size(); 16 result[j++] = l.remove(i); 17 } 18 return result; 19 }
对该方法进行测试,输入人数n=5,报数m=2,输出结果为:
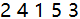
可以看到该结果与原先分析得出的结果一致。
输入人数n=41,报数m=3,输出结果为:
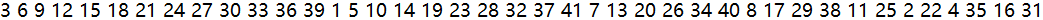
可以看到,结果的最后两个编号为16和31。这就是约瑟夫将朋友与自己安排在第16个与第31个位置,最终逃过了死亡游戏的原因。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号