逻辑回归---梯度下降法

前言：

线性关系主要解决一类事物的特点，而逻辑回归注重于解决分类问题，试图寻找多种事物的边界所在，因此掌握逻辑回归是十分必要的！

正文：

#老朋友
import matplotlib.pyplot as plt
import numpy as np
#做模型评估的，正确率，召回率等
from sklearn.metrics import classification_report
#数据是否需要标准化，可以做也可以不做
from sklearn import preprocessing
#False代表不做,True代表做
#做标准化会使数据变得更加准确更加平滑，推荐做
scale = True

#载入数据
data = np.genfromtxt("LR-testSet.csv",delimiter = ",")
#切分数据，从第1列到最后一列但不包括最后一列
x_data = data[:,:-1]
#最后一列
y_data = data[:,-1]
#定义画图函数
def plot():
    x0 = []
    x1 = []
    y0 = []
    y1 = []
    #切分不同类别的数据
    #有多少数据，循环多少次
    for i in range(len(x_data)):
        #如果数据属于y=0这个类别
        if y_data[i] == 0:
            #把每行第一个数据送给x0
            x0.append(x_data[i,0])
            #把每行第二个数据送给y0
            y0.append(x_data[i,1])
        #如果这个数据属于y=1这个类别
        else:
            #把每行第一个数据送给x0
            x1.append(x_data[i,0])
            #把每行第二个数据送给y0
            y1.append(x_data[i,1])
    #开始画图
    #把属于0的点画成点
    scatter0 = plt.scatter(x0,y0,c = 'b',marker = 'o')
    #把属于1的点画成叉
    scatter1 = plt.scatter(x1,y1,c = 'r',marker = 'x')
    #画图例
    #handles表示你要画图例的数据，labels是图例的名称，loc=‘best’表示自动适配
    plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')
plot()
plt.show()

执行效果如下：

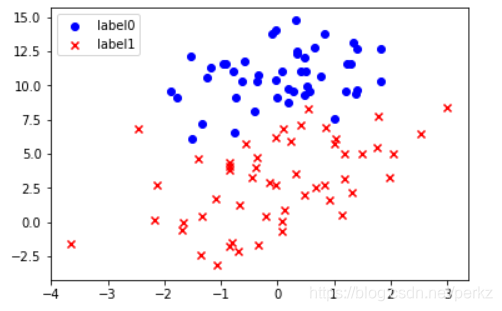
#数据处理，添加偏置项
x_data = data[:,:-1]
#这里注意要给y_data增加维度，让他也变成二维数据来适配函数mat
y_data = data[:,-1,np.newaxis]

print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
#给样本添加偏置项
#concatenate函数可以改变axis的值来进行数据拼接
#axis的值为0时，不改变列数，将数据向下拼接
#axis的值为1时，不改变行数，将数据向右拼接
X_data = np.concatenate((np.ones((100,1)),x_data),axis=1)
print(X_data.shape)

打印出来的data格式如下：

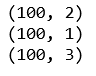
#预测函数
def sigmoid(x):
    return 1.0/(1+np.exp(-x))
 
#代价函数
def cost(xMat,yMat,ws):
    #函数multiply是按位相乘
    left = np.multiply(yMat,np.log(sigmoid(xMat*ws)))
    right = np.multiply(1-yMat,np.log(1-sigmoid(xMat*ws)))
    #返回公式
    return np.sum(left + right) / -(len(xMat))
    
 def gradAscent(xArr,yArr):
    if scale == True:
        xArr = preprocessing.scale(xArr)
    #将数据变成矩阵形式
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    #定义学习率
    lr = 0.001
    #定义循环次数
    epochs = 10000
    #将代价函数的值定义在一个列表
    costList = []
    #计算数据的行列数
    #行代表数据个数，列代表权值个数
    m,n = np.shape(xMat)
    #初始化权值
    ws = np.mat(np.ones((n,1)))
    
    for i in range(epochs+1):
        #xMat和weights矩阵相乘
        h = sigmoid(xMat*ws)
        #计算误差
        #给xMat的矩阵进行转置，才能进行正常的矩阵乘法
        #h-yMat的格式是100*1，xMat.T的矩阵的格式是3*100
        ws_grad = xMat.T*(h-yMat)/m
        #更新ws的值
        ws = ws-lr*ws_grad
        #循环每进行50次，就将更新好的代价函数值代入
        if i%50 == 0:
            costList.append(cost(xMat,yMat,ws))
    return ws,costList

#训练模型，得到权值和cost值的变换
#注意这里的X_data是大写字母
ws,costList = gradAscent(X_data,y_data)
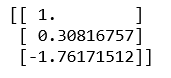
print(ws)

训练后的权值如下：

#不进行数据标准化时
if scale == False:
    #画图决策边界
    plot()
    x_test = [[-4],[3]]
    y_test = (-ws[0]-x_test*ws[1])/ws[2]
    plt.plot(x_test,y_test,'k')
    plt.show()

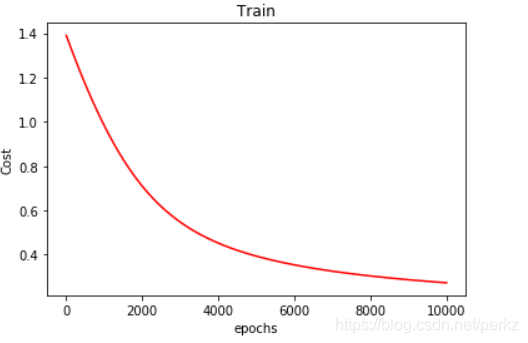
#画图 loss值的变化
#定义图像范围
x = np.linspace(0,10000,201)
#给图像起名贴标签
plt.plot(x,costList,c = 'r')
plt.title('Train')
plt.xlabel('epochs')
plt.ylabel('Cost')
plt.show()

图片展示如下：

#预测
def predict(x_data,ws):
    if scale == True:
        x_data = preprocessing.scale(x_data)
    xMat = np.mat(x_data)
    ws = np.mat(ws)
    return [1 if x>=0.5 else 0 for x in sigmoid(xMat*ws)]
predictions = predict(X_data,ws)
#classification_report计算准确率，召回率
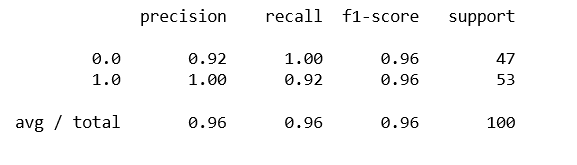
print(classification_report(y_data,predictions))

三种率运算如下：

总结：

可以看出工作量很高，检查很频繁，容易报错，尤其要求对参数格式的转化，期待sklearn库能使工作变得轻松愉悦！