线回与非线回---线性回归标准方程法
前言:
解决线性回归问题不仅可以使用梯度下降法,还可以使用标准方程法,今天我将尝试用标准方程法来解决问题
正文:
#老朋友就不介绍了
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
#载入数据
data = np.genfromtxt("data.csv",delimiter = ",")
#增加维度
x_data = data[:,0,np.newaxis]
y_data = data[:,1,np.newaxis]
#描点画图
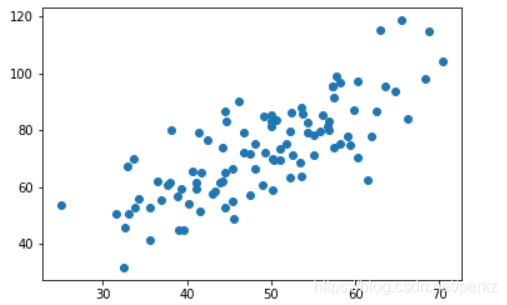
plt.scatter(x_data,y_data)
plt.show()
图片展示:
#np.mat函数用来把数据转化为数组矩阵
print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
#给样本添加偏置项
#用concatenate函数来合并项
#np.ones函数来创建全为1数组矩阵
x_data = np.concatenate((np.ones((100,1)),x_data),axis = 1)
print(x_data.shape)
图片显示如下:
可以看到x_data修改后的格式

#用标准方程来求参数
def weights(xArr,yArr):
#用mat函数来生成矩阵
xMat = np.mat(xArr)
yMat = np.mat(yArr)
xTx = xMat.T*xMat
#矩阵乘法
#用linalg.det函数来计算矩阵的值,如果值为0.说明该矩阵没有逆矩阵
if np.linalg.det(xTx) == 0.0:
print("this matrix cannot do innverse")
return
#xTx.I是xTx的逆矩阵
#xtx.T是xTx的转置矩阵
#通过公式计算出ws,也就是方程各个参数的值
#ws的值应为多个数值,即方程中未知参数的总量
ws = xTx.I*xMat.T*yMat
return ws
#代入我们的数据,并用写好的函数来计算ws的值
ws = weights(x_data,y_data)
print(ws)
结果如下:

#把x_data的范围固定20~80
x_test = np.array([[20],[80]])
#用ws中求出来的参数值,计算y的值
y_test = ws[0] + x_test*ws[1]
#描点描线
plt.plot(x_data,y_data,'b.')
plt.plot(x_test,y_test,'r')
#画图
plt.show()

总结:
通过标准方程法同样可以解决问题,且较为简单,但对于多参数问题,则梯度下降法比较合适!




