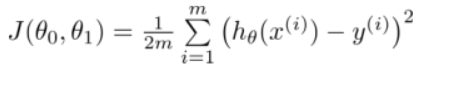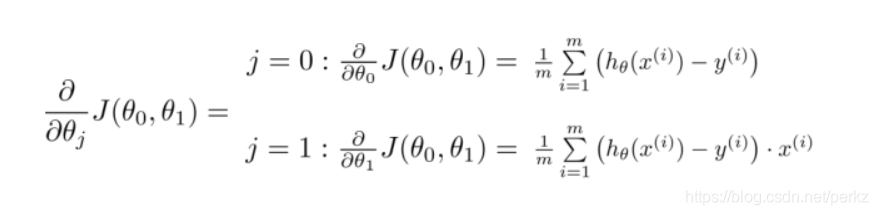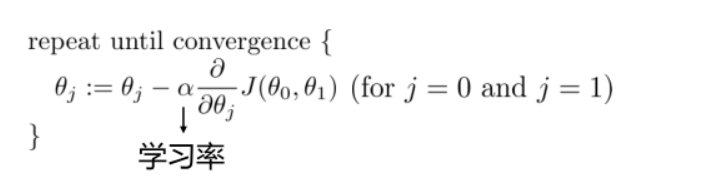线回与非线回---梯度下降法--多元线性回归
前言:
这次我来使用梯度下降法来解决多元线性回归问题,实际问题中每个事物都带有很多属性,一个参数往往只出现于理想情况,因此解决多元问题是很重要的。
正文:
import numpy as np
from numpy import genfromtxt
#genfromtxt使用的比较频繁
#就把他拉出来单独用了,不用次次都调用np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#mpl_toolkits.mplot3d是用来画3d图的
#参数多了,就需要多维平面来解决问题了
#读入你需要使用的数据
data=genfromtxt("Delivery.csv",delimiter=',')
print(data)
数据展示如下:
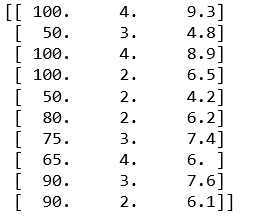
#切分数据
#这里我希望y_data代表的是theta0
#x_data代表除theta0以外的参数
#因此切分数据时把第一和第二列给x_data,最后一列给y_data
#代表了最后一列是theta0的值,其余为其他参数的值
x_data = data[:,:-1]
y_data = data[:,-1]
print(x_data)
print(y_data)
数据切分情况,看得出来成功切成了两部分:

#学习率
lr = 0.0001
#设置参数,只不过参数由一元变成了多元,想要几个就设置几个
theta0 = 0
theta1 = 0
theta2 = 0
#最大迭代次数
epochs = 1000
#最小二乘法,这一步仍然是在算j(theta)
def compute_error(theta0,theta1,theta2,x_data,y_data):
totalError = 0
for i in range(0,len(x_data)):
totalError +=(y_data[i]-(theta1*x_data[i,0]+theta2*x_data[i,1]+theta0))**2
return totalError/float(len(x_data)
#这个函数和一元函数的相似,也是用来求各个参数的值
def gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs):
#计算总数据量
m = float(len(x_data)
#循环开始,epochs的值自己设置
for i in range(epochs):
theta0_grad = 0
theta1_grad = 0
theta2_grad = 0
#下面的循环是来给每个参数进行求偏导
#用已经求好的公式,把数据进行带入即可
for j in range(0,len(x_data)):
theta0_grad += -(1/m)*(y_data[j]-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0))
theta1_grad += -(1/m)*(x_data[j,0])*(y_data[j]-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0))
theta2_grad += -(1/m)*(x_data[j,1])*(y_data[j]-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0))
#上面的循环结束后,再开始更新b和k的值
#符合同步更新的原则,先求值后赋值
#当然这里的参数多了一个,因为是多元函数嘛
theta0 = theta0 - (lr*theta0_grad)
theta1 = theta1 - (lr*theta1_grad)
theta2 = theta2 - (lr*theta2_grad)
return theta0,theta1,theta2
#这里开始写主程序,用上面写好的函数来进行求参数值
print("strating theta0 = {0},theta1 = {1},theta2 = {2},error = {3}"
.format(theta0,theta1,theta2,compute_error(theta0,theta1,theta2,x_data,y_data)))
print("running...")
theta0,theta1,theta2 = gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs)
print("after {0} theta0={1},theta1={2},theta2={3},error = {4}"
.format(epochs,theta0,theta1,theta2,compute_error(theta0,theta1,theta2,x_data,y_data)))
更新后的参数值:

#这个add_subplot函数暂时没有弄清111到底有什么作用
#但是应该和起始位置有关,网上的回答有些模糊
ax = plt.figure().add_subplot(111,projection = '3d')
#scatter函数里,c代表颜色,marker代表标记点的形状,s代表什么暂不清楚,但默认值是20
ax.scatter(x_data[:,0],x_data[:,1],y_data,c = 'r',marker = 'o',s = 100)
#具体细分x轴和y轴的数据,z轴的值用x,y的值来求
x0= x_data[:,0]
x1 = x_data[:,1]
#生成网格矩阵
#meshgrid函数很方便,直接把切割好的数据放进去
#可以帮你自动生成网格图
x0,x1 = np.meshgrid(x0,x1)
z = theta0+x0*theta1+x1*theta2
#用plot_surface函数来画出3d图
ax.plot_surface(x0,x1,z)
#给你的x,y,z轴起名字
ax.set_xlabel('miles')
ax.set_ylabel('num of deliveries')
ax.set_zlabel('time')
#显示你的图像
plt.show()
图片展示如下:
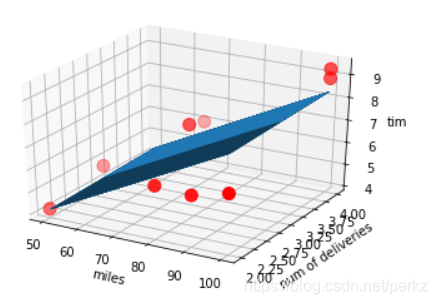
总结:
这次有两个问题没有很明白,一个是add_subplot里的111到底是干什么的,一个是ax.scatter里的s究竟代表什么,网上的解释究竟代表什么不是很清楚,希望有高手看到可以帮忙解决一下,如果我解决处理了会在评论里发出来!
顺便po两个公式图: