60个必备NOIP模板(附超详解释)
不定期更细中。。。。。。
声明1:由于js的问题导致VIEW CODE按钮只能点“I”附近才能展开代码
声明2:为了排版的美观,所有的解释以及需要留意的地方我都放在代码中了
声明3:以下所有代码均是已经AC的,请各位放心食用
杂项
快速读入(包括符号)
long long read(){
long long x=0,f=1;
char c=getchar();
while((c<'0'||c>'9')&&c!='-')c=getchar();
if(c=='-')f=-1,c=getchar();
while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
ST表
//交LG的话记得加快读~~~
#include<bits/stdc++.h>
using namespace std;
int n,m,f[5000005][20];//f[i][j]为从i开始(2^j)-1的最大值
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>f[i][0];
}
for(int k=1;k<=20;k++){
for(int i=1;i<=n-(1<<k)+1;i++){
f[i][k]=max(f[i][k-1],f[i+(1<<(k-1))][k-1]);//将区间拆成两半[i,i+2^j-1]和[i+2^(j-1),j-1]
}
}//如果是先枚举i那么在f[1][2]的时候会不知道f[2][1]的值
for(int i=1;i<=m;i++){
int le,ri;cin>>le>>ri;
int t=log(ri-le+1)/log(2);//换底公式即log以2为ri-le+1的对数,找到最大的k
printf("%d\n",max(f[le][t],f[ri-(1<<t)+1][t]));//左右两半区间查询
//记得+1如1~5:log2(5)=2,f[1][2]为1~4的max而后半段要2~5,5-2^2=1所以要加1!!!
}
}
线段树1
#include<bits/stdc++.h>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m,a[100005];
struct node{
ll sum,add;
ll l,r;
}t[1000005];
ll read(){
ll x=0;char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
void build(ll p,ll l,ll r){
t[p].l=l,t[p].r=r;
if(l==r){t[p].sum=a[l];return ;}
ll mid=(l+r)>>1;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
t[p].sum=t[p*2].sum+t[p*2+1].sum;
}
void spread(ll p){
if(t[p].add){
t[p*2].sum+=(ll)t[p].add*(t[p*2].r-t[p*2].l+1);//ll!!!
t[p*2+1].sum+=(ll)t[p].add*(t[p*2+1].r-t[p*2+1].l+1);
t[p*2].add+=t[p].add;//别忘了
t[p*2+1].add+=t[p].add;
t[p].add=0;
}
}
void add(ll p,ll l,ll r,ll k){
if(t[p].l>=l&&t[p].r<=r){
t[p].add+=k;
t[p].sum+=(ll)k*(t[p].r-t[p].l+1);//不要忘了
return ;
}
spread(p);
ll mid=(t[p].l+t[p].r)>>1;//记得是在这个节点记录的区间的中点
if(l<=mid)add(p*2,l,r,k);//注意是l<=mid否则当修改区间横跨了mid时就不会进行任何操作
if(r>mid)add(p*2+1,l,r,k);
t[p].sum=t[p*2].sum+t[p*2+1].sum;//还要记得修改sum
}
ll ask(ll p,ll l,ll r){
if(t[p].l>=l&&t[p].r<=r){
return t[p].sum;
}
spread(p);
t[p].sum=t[p*2].sum+t[p*2+1].sum;//每次spread之后都要从新统计sum!
ll mid=(t[p].r+t[p].l)>>1;
ll val=0;
if(l<=mid)val+=ask(p*2,l,r);//如果这里修改为l~mid下面改成mid+1~r,则下一次进入ask函数的mid
//就会比这一次的r大了,因为mid是该节点的中间点,mid=(t[p].r+t[p].l)>>1
//后来我想改成mid=(l+r)>>1配套l~mid和mid+1~r,但这样会出现更严重的问题,
//假设询问的区间全部位于整棵树的左子树,这个时候会出现
//到整棵树的右子树中去求询问区间的右半边的情况,找了个寂寞!(感谢mrgg的提醒)
if(r>mid)val+=ask(p*2+1,l,r);
return val;
}
int main(){
8 cin>>n>>m;
for(ll i=1;i<=n;i++){
a[i]=read();
}
build(1,1,n);
for(ll i=1;i<=m;i++){
ll ty=read();
if(ty==1){
ll cn=read(),cm=read(),cw=read();
add(1,cn,cm,cw);
}
else {
ll cn=read(),cm=read();
cout<<ask(1,cn,cm)<<endl;
}
}
}
线段树2
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,m,a[1000005],mod;
struct node{
ll sum,l,r,mu,add;
}t[1000005];
ll read(){
ll x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
void build(ll p,ll l,ll r){
t[p].l=l,t[p].r=r;t[p].mu=1;
if(l==r){t[p].sum=a[l]%mod;return ;}
ll mid=(l+r)>>1;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
t[p].sum=(t[p*2].sum+t[p*2+1].sum)%mod;
}
void spread(ll p){
t[p*2].sum=(ll)(t[p].mu*t[p*2].sum+((t[p*2].r-t[p*2].l+1)*t[p].add)%mod)%mod;
t[p*2+1].sum=(ll)(t[p].mu*t[p*2+1].sum+(t[p].add*(t[p*2+1].r-t[p*2+1].l+1))%mod)%mod;
t[p*2].mu=(ll)(t[p*2].mu*t[p].mu)%mod;
t[p*2+1].mu=(ll)(t[p*2+1].mu*t[p].mu)%mod;
t[p*2].add=(ll)(t[p*2].add*t[p].mu+t[p].add)%mod;
t[p*2+1].add=(ll)(t[p*2+1].add*t[p].mu+t[p].add)%mod;
t[p].mu=1,t[p].add=0;
}
void add(ll p,ll l,ll r,ll k){
if(t[p].l>=l&&t[p].r<=r){
t[p].add=(t[p].add+k)%mod;
t[p].sum=(ll)(t[p].sum+k*(t[p].r-t[p].l+1))%mod;//只要加上增加的就好
return ;
}
spread(p);
t[p].sum=(t[p*2].sum+t[p*2+1].sum)%mod;
ll mid=(t[p].l+t[p].r)>>1;
if(l<=mid)add(p*2,l,r,k);
if(mid<r)add(p*2+1,l,r,k);
t[p].sum=(t[p*2].sum+t[p*2+1].sum)%mod;
}
void mu(ll p,ll l,ll r,ll k){
if(t[p].l>=l&&t[p].r<=r){
t[p].add=(t[p].add*k)%mod;//比较重要的一步,add要在这里乘上k,因为后面可能要加其他的数而那些数其实是不用乘k的
t[p].mu=(t[p].mu*k)%mod;
t[p].sum=(t[p].sum*k)%mod;
return ;
}
spread(p);
t[p].sum=t[p*2].sum+t[p*2+1].sum;
ll mid=(t[p].l+t[p].r)>>1;
if(l<=mid)mu(p*2,l,r,k);
if(mid<r)mu(p*2+1,l,r,k);
t[p].sum=(t[p*2].sum+t[p*2+1].sum)%mod;
}
ll ask(ll p,ll l,ll r){
if(t[p].l>=l&&t[p].r<=r){
return t[p].sum;
}
spread(p);
ll val=0;
ll mid=(t[p].l+t[p].r)>>1;
if(l<=mid)val=(val+ask(p*2,l,r))%mod;
if(mid<r)val=(val+ask(p*2+1,l,r))%mod;
return val;
}
int main(){
cin>>n>>m>>mod;
for(int i=1;i<=n;i++){
a[i]=read();
}
build(1,1,n);
for(int i=1;i<=m;i++){
int ty=read();
if(ty==1){
ll cn=read(),cm=read(),cw=read();
mu(1,cn,cm,cw);
}else if(ty==2){
ll cn=read(),cm=read(),cw=read();
add(1,cn,cm,cw);
}else {
ll cn=read(),cm=read();
cout<<ask(1,cn,cm)<<endl;
}
}
}
悬线法
#include<bits/stdc++.h>
using namespace std;
int n,m,a[1005][1005],l[1005][1005],r[1005][1005],up[1005][1005];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
char ch;cin>>ch;
if(ch=='F')a[i][j]=1;
r[i][j]=l[i][j]=j,up[i][j]=1;
}
}
for(int i=1;i<=n;i++){
for(int j=2;j<=m;j++){
if(a[i][j]==a[i][j-1]&&a[i][j]==1)l[i][j]=l[i][j-1];
}
for(int j=m-1;j>=1;j--){
if(a[i][j]==a[i][j+1]&&a[i][j]==1)r[i][j]=r[i][j+1];
}
}
int ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(i>1&&a[i][j]==a[i-1][j]&&a[i][j]==1){//是>1才进去但是i=1时还是要做的
r[i][j]=min(r[i][j],r[i-1][j]);
l[i][j]=max(l[i][j],l[i-1][j]);
up[i][j]=up[i-1][j]+1;
}
ans=max(ans,(r[i][j]-l[i][j]+1)*up[i][j]);
}
}
cout<<ans;
}
哈夫曼树
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m;
priority_queue<pair<int,int> >dui;
signed main(){
cin>>n>>m;int w;
for(int i=1;i<=n;i++){
cin>>w;
dui.push(make_pair(-w,-1));
}
while((dui.size()-1)%(m-1))dui.push(make_pair(-0,-1));//最后一次合并要满足=0 因为每次合并要减少k-1个节点要将n个节点合并成1个
//题解里的解释:因为每次都是将k个节点合并为1个(减少k-1个),一共要将n个节点合并为1个,如果(n-1)%(k-1)!=0
//则最后一次合并时不足k个。也就表明了最靠近根节点的位置反而没有被排满,因此我们需要加入k-1-(n-1)%(k-1)个空节点
//使每次合并都够k个节点(也就是利用空节点将其余的节点挤到更优的位置上)。
int ans=0;
while(dui.size()>=m){
int re=0,h=-0;
for(int i=1;i<=m;i++){
int x=dui.top().first,y=dui.top().second;dui.pop();
re+=x;
h=min(h,y);
}
ans+=re;
dui.push(make_pair(re,h-1));
}
cout<<-ans<<endl<<-dui.top().second-1;
}
后序遍历
#include<bits/stdc++.h>
using namespace std;
char q[1000005],z[1000005];
int len;
int find(char k){
for(int i=1;i<=len;i++)if(q[i]==k)return i;
}
void dfs(int l1,int r1,int l2,int r2){
int m=find(z[r2]);
cout<<q[m];
if(m>l1)dfs(l1,m-1,l2,r2-r1+m-1);//有左子树
if(r1>m)dfs(m+1,r1,l2+m-l1,r2-1);
}
//r2-(r1-m+1)
//r2-r1+m-1
//l2+(m-r1)
//l2+m-r1
int main(){
scanf("%s",q+1);scanf("%s",z+1);
len=strlen(q+1);
dfs(1,len,1,len);
}
后缀表达式
#include<bits/stdc++.h>
using namespace std;
char a[1005];
int sum,k;
stack <int> stk;
int main(){
gets(a);
for(int i=0;a[i]!='@';i++){
if(a[i]=='.'){
sum=0,k=1;
for(int j=i-1;j>=0&&a[j]>='0'&&a[j]<='9';j--) sum=sum+(a[j]-48)*k,k*=10;
stk.push(sum);
continue;
}
if(a[i]>='0'&&a[i]<='9') continue;
sum=stk.top();
stk.pop();
if(a[i]=='+') sum=stk.top()+sum;
if(a[i]=='-') sum=stk.top()-sum;
if(a[i]=='*') sum=stk.top()*sum;
if(a[i]=='/') sum=stk.top()/sum;
stk.pop();
stk.push(sum);
}
printf("%d",stk.top());
return 0;
}
中缀表达式转后缀表达式
#include<bits/stdc++.h>
#define M 10007
using namespace std;
int n;
char ss[10000005];
stack<char>dui;
int main(){
cin>>n;
scanf("%s",ss +1);
string s=".";
for(int i=1;i<=n;i++){
if(ss[i]=='('||ss[i]=='*'){
dui.push(ss[i]);
}
if(ss[i]=='+'){
while(dui.size()&&dui.top()=='*'){//直到找到优先级更低的符号
s+=dui.top();
dui.pop();
}
dui.push('+');
}
if(ss[i]==')'){
while(dui.size()&&dui.top()!='('){
s+=dui.top();
dui.pop();
}
dui.pop();
}
if(ss[i]!='('&&ss[i]!=')'){
s+='.';
}
}
while(dui.size())s+=dui.top(),dui.pop();
cout<<s<<endl;
}
/* 8
+*+(*+)*
下面的话来自题解区:
转换过程需要用到栈,具体过程如下:
1)如果遇到操作数,我们就直接将其输出。
2)如果遇到操作符,则我们将其放入到栈中,遇到左括号时我们也将其放入栈中。
3)如果遇到一个右括号,则将栈元素弹出,将弹出的操作符输出直到遇到左括号为止。注意,左括号只弹出并不输出。
4)如果遇到任何其他的操作符,如(“+”, “*”,“(”)等,从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后,才将遇到的操作符压入到栈中。有一点需要注意,只有在遇到" ) "的情况下我们才弹出" ( ",其他情况我们都不会弹出" ( "。
5)如果我们读到了输入的末尾,则将栈中所有元素依次弹出。
备注:本题中我们用一个"."来代表数字。扫描整个表达式(读入的字符串),如果当前位置不是括号(既不是左括号也不是右括号),就在后缀表达式里填一个"."表示这里应有一个数字。*/
科学的整数二分模板
int l=0,r=1e6+1,mid;
while(l<r){
mid=(l+r)>>1;
if(check(mid)) r=mid;
else l=mid+1;
}
return l;
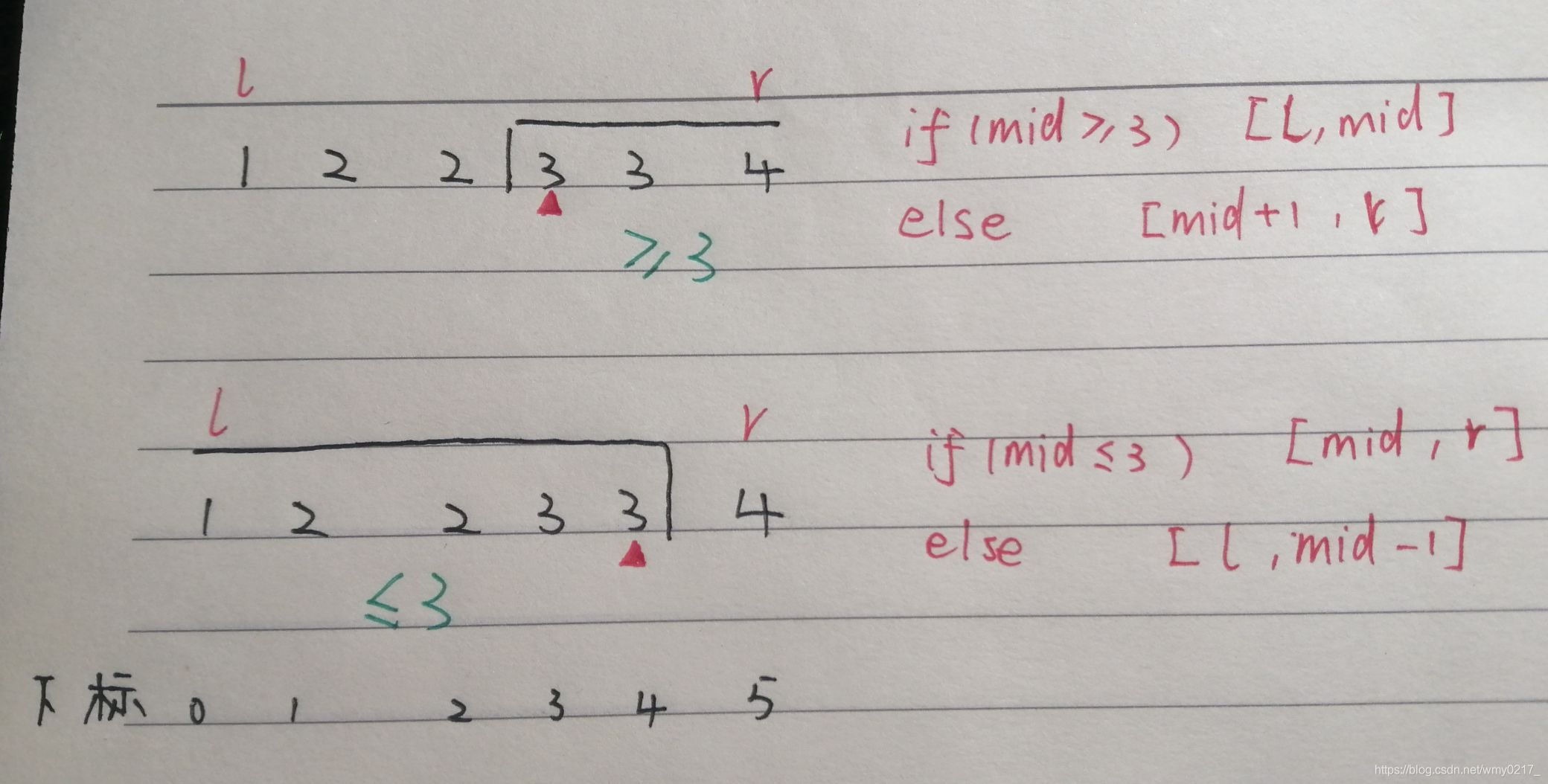
(图片备用链接:https://cdn.luogu.com.cn/upload/image_hosting/jj8qtvuh.png)
小数二分
double l=1,r=2000;
while(r-l>1e-5){
double mid=(l+r)/2;
if(check(mid))l=mid;
else r=mid;
}
printf("%d\n",r);
逆序对
#include<iostream>
using namespace std;
long long t[1000005],ans=0;
long long n,a[1000005];
void merge(int l,int r){//归并大法
if(l==r)
return;
int mid=(l+r)/2;
merge(l,mid);//用分治的思想,先分离,再合并
merge(mid+1,r);
int i=l,j=mid+1,p=l;
while(i<=mid&&j<=r){
if(a[i]>a[j]){
t[p++]=a[j++];
ans+=mid-i+1;//此时两边都是排好序了的,当前面的序列中有一个数大于后面的一个数时,前面序列中剩下的数都大于这个数,共mid-i+1个
}
else
t[p++]=a[i++];
}
while(i<=mid)
t[p++]=a[i++];//把序列中剩下的数存入t
while(j<=r)
t[p++]=a[j++];
for(i=l;i<=r;i++)
a[i]=t[i];//t中的数要回到a中
}
int main(){
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
merge(1,n);//调用merge
cout<<ans<<endl;
return 0;
}
树状数组1
#include<bits/stdc++.h>
using namespace std;
int n,m,a[5000005],sum[5000005];
int read(){
int x=0;char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
int lowbit(int x){return x&(-x);}
void add(int x,int k){while(x<=n)sum[x]+=k,x+=lowbit(x);}
int getsum(int x){
int re=0;
while(x!=0){
re+=sum[x];
x-=lowbit(x);
}
return re;
}
int main(){
n=read(),m=read();
for(int i=1;i<=n;i++)a[i]=read();
for(int i=1;i<=n;i++)add(i,a[i]);
int ty,x,y;
for(int i=1;i<=m;i++){
scanf("%d%d%d",&ty,&x,&y);
if(ty==1)add(x,y);
else cout<<getsum(y)-getsum(x-1)<<endl;
}
}
//单点修改区间查询
树状数组2
#include<bits/stdc++.h>
using namespace std;
int n,m,a[500005],sum[500005];
int lowbit(int x){return x&(-x);}
void add(int x,int k){while(x<=n)sum[x]+=k,x+=lowbit(x);}
int getsum(int x){int re=0;while(x)re+=sum[x],x-=lowbit(x);return re;}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
int ty,x,y,k;
for(int i=1;i<=m;i++){
cin>>ty;
if(ty==1){
cin>>x>>y>>k;
add(x,k);
add(y+1,-k);
}else {
cin>>x;
cout<<a[x]+getsum(x)<<endl;
}
}
}
//区间修改单点查询,我们不可能一个个去修改,于是考虑差分,想到这问题迎刃而解,区间修改时只需修改x和y+1即可,最后求个sum+a[x]即为答案
A*
#include<bits/stdc++.h>
using namespace std;
int lim,mp[10][10];
const int n=5;
const int dx[10]={0,1,1,-1,-1,2,2,-2,-2};
const int dy[10]={0,2,-2,2,-2,1,-1,1,-1};
const int st[7][7]={
{0,0,0,0,0,0},
{0,1,1,1,1,1},
{0,0,1,1,1,1},
{0,0,0,2,1,1},
{0,0,0,0,0,1},
{0,0,0,0,0,0}
};
int diff(){
int re(0);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(mp[i][j]!=st[i][j])++re;
}
}
return re;
}
bool ans;
bool pen(int x,int y){
if(x<1||x>n||y<1||y>n)return 0;
return 1;
}
void dfs(int dep,int x,int y){
if(ans)return ;
if(dep==lim){//必须是==,否则就成正常的搜索了......
if(!diff()){
ans=1;
printf("%d\n",lim);
}
return ;
}
for(int i=1;i<=8;i++){
int xx=x+dx[i],yy=y+dy[i];
if(pen(xx,yy)){
swap(mp[x][y],mp[xx][yy]);
int now=diff();
if(now+dep<=lim)dfs(dep+1,xx,yy);
swap(mp[x][y],mp[xx][yy]);
}
}
}
int main(){
int tt;
cin>>tt;
while(tt--){
int stax,stay;
char ch;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>ch;
if(ch=='*')stax=i,stay=j,mp[i][j]=2;
else mp[i][j]=ch-'0';
}
}
if(!diff()){printf("-1\n");continue;}
for(lim=1;lim<=15;lim++){
dfs(0,stax,stay);
}
if(!ans)printf("-1\n");
ans=0;
}
}
DP
DD大牛的背包九讲(原版找不到了,将就一下)
https://blog.csdn.net/qq_41267618/article/details/89403294
01背包
不要求正好装满
#include<iostream>
using namespace std;
int n,V,w[1000000],v[1000000],dp[1000000];
int main(){
cin>>n>>V;
for(int i=1;i<=n;i++){
cin>>w[i]>>v[i];
}
for(int i=1;i<=n;i++){
for(int j=V;j>=w[i];j--){
dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
}
}
cout<<dp[V]<<endl;
}
如果要求正好装满。。。
//其实两种做法的区别仅仅是初始化的不同,当要求正好装满时,仅将dp[0]赋值为0,其它都是-INF
//因为只有dp[0]合法(什么都不装相当于装了一个体积为0的物品)
//比如现在有v[i]=3的一个物品,则dp[3]可以正好装下它
//所以dp[3]此时不再是-INF,最后只要检查一下是否dp[V]>0即可
//这个小技巧完全可以推广到其它类型的背包问题
//下文未作说明默认不必放满
#include<iostream>
using namespace std;
int n,V,w[1000000],v[1000000],dp[1000000];
int main(){
cin>>n>>V;
for(int i=1;i<=n;i++){
cin>>w[i]>>v[i];
}
for(int i=1;i<=V;i++)dp[i]=-0x7fffffff
for(int i=1;i<=n;i++){
for(int j=V;j>=w[i];j--){
dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
}
}
cout<<dp[V]<<endl;
}
完全背包
//完全背包与01背包的区别是完全背包的物品有无限个,但01背包仅有一个
//考虑01背包的转移为什么是倒序,因为正序转移有可能造成同一个物品被考虑多次
//这正是完全背包要求的,比如w[3]=3,dp[1]=5,则在dp[4]、dp[7]都会考虑一遍3号物品
#include<iostream>
using namespace std;
int n,V,v[1000000],w[1000000],dp[1000000];
int main(){
cin>>n>>V;
for(int i=1;i<=n;i++){
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++){
for(int j=w[i];j<=V;j++){
dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
}
}
cout<<dp[V]<<endl;
}
多重背包
//多重背包在完全背包的基础上更近一步给出了物品的个数
//多重背包可以将每件物品拆成单个的物品跑01背包,但数据上规模会TLE
//这个时候考虑二进制优化,因为任何数都可以用二进制表示,如6件拆成2^0,2^1,3(surplus)
#include<iostream>
using namespace std;
int n,V,w[1000000],v[1000000],cnt,dp[1000000];
int main(){
cin>>n>>V;
int cv,cw,c,k;
for(int i=1;i<=n;i++){
cin>>cv>>cw>>c;
k=1;
while(k<=c){
w[++cnt]=cw*k;
v[cnt]=cv*k;
c-=k;
k=k<<1;//就是k*=2,进行二进制拆分
}
if(c){
w[++cnt]=cw*c;
v[cnt]=cv*c;
}
}
for(int i=1;i<=cnt;i++){
for(int j=V;j>=w[i];j--){//倒序跑01背包
dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
}
}
cout<<dp[V];
}
二维费用背包
#include<iostream>
using namespace std;
int n,V,M,v[1000000],m[1000000],w[1000000],dp[10000][10000];
int main(){
cin>>n>>V>>M;
for(int i=1;i<=n;i++){
cin>>m[i]>>v[i]>>w[i];
}
for(int i=1;i<=n;i++){
for(int j=M;j>=m[i];j--){//可以与下面的for交换位置
for(int k=V;k>=v[i];j--){
dp[j][k]=max(dp[j][k],dp[j-m[i]][k-v[i]]+w[i]);
//二维费用背包有两个限制条件,只需增加一维即可,当发现题目是由熟悉的动态规划题目变形得来的时
//在原来的状态中加一纬以满足新的限制是一种比较通用的方法
}
}
}
cout<<dp[V][M];
}
分组背包
#include<iostream>
using namespace std;
int n,V,m,dp[1000000];
struct node{
int cnt,v[1000],w[1000];
}bag[10000];
int main(){
cin>>n>>m>>V;
for(int i=1;i<=m;i++){
cin>>bag[i].cnt;
for(int j=1;j<=bag[i].cnt;j++){
cin>>bag[i].v[j]>>bag[i].w[j];
}
}
for(int i=1;i<=m;i++){
for(int j=V;j>=1;j--){//显然是01背包~
for(int k=1;k<=bag[i].cnt;k++){//分组枚举(注意先枚举空间)
if(j<bag[i].v[j])continue;
dp[j]=max(dp[j],dp[j-bag[i].v[k]]+bag[i].w[k]);
}
}
}
cout<<dp[V]<<endl;
}
有依赖的背包问题(树形DP)
//将主件视为根,将附件视为儿子,直接树形DP(金明的预算方案)
#include<bits/stdc++.h>
using namespace std;
int n,m,v[100000],ji,head[100000],dp[1000][100000],w[100000];
struct node{
int to,next;
}ed[100000];
int add(int p,int q){
ed[++ji].to=q;
ed[ji].next=head[p];
head[p]=ji;
}
void tree_dp(int k,int le){
for(int i=head[k];i;i=ed[i].next){
int y=ed[i].to;
tree_dp(y,le-v[k]);
for(int j=le;j>=v[k];j--){
for(int t=j-v[k];t>=0;t--)
dp[k][j]=max(dp[k][j],dp[k][j-t]+dp[y][t]);//枚举花去金额t来寻找最大满意度
}//dp[i][j]为主件为i时剩余金钱为j时的满意度(v*w)
}
for(int i=le;i>=v[k];i--)dp[k][i]+=w[k];//k为主件当然要算入k贡献的满意度
}
int main(){
cin>>m>>n;
m/=10;
int q;
for(int i=1;i<=n;i++){
cin>>v[i]>>w[i]>>q;//价格,重要程度,对应的主件
v[i]/=10;
w[i]*=v[i];//预处理w为买i所贡献的满意度
add(q,i);
}
tree_dp(0,m);
cout<<dp[0][m]*10<<endl;
}
LIS(最长上升子序列)
//维护一个单调上升的序列,如果当期的数比序列最后一个元素大则加入末尾
//否则二分一个合适的位置替换掉那个元素,这种替换不会增加序列的长度,但是这一步的意义
//在于记录最小序列,代表了一种“最可能性”。注意数组中的序列并不一定是正确的最长上升子序列
//例1,4,7,2,5,9,10,3 序列:1->1,4->1,4,7->1,2,7->1,2,5->1,2,5,9->1,2,5,9,10->1,2,3,9,10
#include<bits/stdc++.h>
using namespace std;
int n,a[100005],f[100005];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];f[i]=0x7ffffff;
}
int len=0;f[0]=0;
for(int i=1;i<=n;i++){
if(f[len]<a[i])f[++len]=a[i];
else {
int l=1,r=len;
while(l<r){
int mid=(l+r)>>1;
if(a[i]<f[mid])r=mid;
//因为要将a[i]插入到f中,且插入位置保证f[mid]>=a[i],所以>a[i]也可能是答案
else l=mid+1;
}
f[l]=a[i];
}
}
cout<<len;
}
LCS(最长公共子序列)
#include<bits/stdc++.h>
using namespace std;
int n,f[100001],a[100001],b[100001],ma[100001];//ma为编号序列
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];ma[a[i]]=i,f[i]=0x7fffffff;
}
for(int i=1;i<=n;i++)cin>>b[i];
f[0]=0;
int len=0;
for(int i=1;i<=n;i++){
if(f[len]<ma[b[i]])f[++len]=ma[b[i]];//比队尾还大
else {
int l=1,r=len;
while(l<r){
int mid=(l+r)>>1;
if(f[mid]<ma[b[i]])l=mid+1;
else r=mid;
}
f[l]=ma[b[i]];
}
}
cout<<len;
}
/*由于数据过大我们在时间和空间上都不能像下面那样做,那怎么办呢
我们发现既然是1到n的排列,那就可以把A离散化,得到B在A序列中的编号,找到一段编号序列的子序列
他是单调递增的,那么就表明对应元素在A和B中是从前往后排列的
这就是我们要的答案,找这段单调递增的序列其实就是LIS哦*/
#include<bits/stdc++.h>
using namespace std;
int n,m,a[2005],b[2005],f[2005][2005];//fij表示到ai和bj的位置且ai必选
inline int read(){
register int x=0;register char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
int main(){
cin>>n>>m;
for(register int i=1;i<=n;++i){
a[i]=read();
}
for(register int i=1;i<=m;++i){
b[i]=read();
}
register int maxn=0;
for(register int i=1;i<=n;++i){
for(register int j=1;j<=m;++j){
if(a[i]==b[j]){
for(register int k=1;k<j;++k){
f[i][j]=max(f[i][j],f[i][k]+1);
}
maxn=max(maxn,f[i][j]);
}else f[i][j]=f[i-1][j];
}
}
cout<<maxn<<endl;
}
LCIS
#include<bits/stdc++.h>
using namespace std;
int n,m,a[505],b[505],g[505][505],f[505][505];
void path(int i,int j){
if(j==0)return ;
path(g[i][j],j-1);
if(g[i][j]!=i){
printf("%d ",a[i]);
}
}
int main(){
cin>>n;for(int i=1;i<=n;i++)cin>>a[i];
cin>>m;for(int j=1;j<=m;j++)cin>>b[j];
int maxn=0,x=0,y=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i]==b[j]){
f[i][j]=1;
for(int k=1;k<i;k++){
if(a[k]<a[i]){
if(f[i][j]<f[k][j-1]+1){
//如果是f[k][j]由于a[1~i]与b[j]不匹配所以这样是错的
f[i][j]=f[k][j-1]+1;
g[i][j]=k;
}
}
}
if(maxn<f[i][j])maxn=f[i][j],x=i,y=j;
}else{
f[i][j]=f[i][j-1];
g[i][j]=i;
}
}
}
cout<<maxn<<endl;
path(x,y);
cout<<endl;
}
/*输出的递归函数path应有两个参数(i,j),表示当前在数组A中位置是i,在数组B中位置是j
我们沿着f[i][j]转移时的路径递归,也就是path(i-1,g[i][j])
若g[i][j]==j,则说明这里是没有增加LCIS长度的转移
应该沿着f[i][j]转移时的路径继续递归,但不输出.直到g[i][j]!=j就输出B[j]*/
数论类
O(1)快速乘
int qmul(int x,int y,int mod){
return (x*y-(long long)((long double)x/mod*y)*mod+mod)%mod;
}
gcd
inline ll gcd(ll a,ll b){
if(a==0)return b;if(b==0)return a;
if(!(a&1)&&!(b&1))return 2*gcd(a>>1,b>>1);
else if(!(a&1))return gcd(a>>1,b);
else if(!(b&1))return gcd(a,b>>1);
else return gcd(abs(a-b),min(a,b));
}//法一是二进制版本,法二三目版本如下
int gcd(int a,int b){
return b>0?gcd(b,a%b):a;
//其实algorithm库里面有__gcd(a,b)函数
线性基
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll p[55],a,n,ans;
void merge(ll k){
for(int i=55;i>=0;i--){//>=0!!!!!!!!
if(!(k>>i))continue;
if(!p[i]){p[i]=k;break;}
k^=p[i];//消去最高位,后面的1不管,这也是为什么线性基不唯一——shuixirui
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a;
merge(a);
}
for(int i=55;i>=0;i--){
if((ans^p[i])>ans)ans^=p[i];
}
cout<<ans;
}
//如果要查询某个数是否能被该线性基表出可以把该数转成二进制
//对于每一位如果为1就XORp[i]如果最后结果为0则可以被表出
裴蜀定理
//裴蜀定理内容ax+by=c,x∈Z*,y∈Z*成立的充要条件是gcd(a,b)∣c,Z* 表示正整数集。
//扩展到求ax+by=c 的最小非负 c,显然 c 要满足 (a,b)|c,所以 c 取 (a,b)是最小的。
#include<bits/stdc++.h>
using namespace std;
int n,a,ans;
int gcd(int a,int b){
if(!b)return a;
return gcd(b,a%b);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){cin>>a;a>0?(a*=1):(a*=(-1));ans=gcd(ans,a);}
cout<<ans;
}
线性素数筛
#include<bits/stdc++.h>
using namespace std;
int n,m,prime[100000005],ji;
bool bo[10000005];
int main(){
cin>>n>>m;
for(int i=2;i<=n;i++){
if(!bo[i])prime[++ji]=i;//不能加括号!!!,每次都要更新!!!
for(int j=1;i*prime[j]<=n;j++){//记得是prime[j]*i,i和j换个位置
bo[i*prime[j]]=1;
if(i%prime[j]==0)break;//期中有其他因子的时候就退出来
}
}
bo[1]=bo[0]=1;
for(int i=1;i<=m;i++){
int cn;cin>>cn;
if(bo[cn])cout<<"No"<<endl;
else cout<<"Yes"<<endl;
}
}
//当你n特别大比如1e12时我们可以这么求出这个数可以被分解成多少个质数:
#include<bits/stdc++.h>
using namespace std;
long long read(){
long long x=0,f=1;
char c=getchar();
while((c<'0'||c>'9')&&c!='-')c=getchar();
if(c=='-')f=-1,c=getchar();
while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
long long T,n,ans;
int main(){
T=read();
while(T--){
n=read();
ans=0;
for(long long i=2;i*i<=n;++i)
while(!(n%i)){
n/=i;
ans++;
}
if(n>1)ans++;
if(ans==2)printf("Bob\n");
else printf("Alice\n");
}
return 0;
}
快速幂
#include<bits/stdc++.h>
#define ll long long
using namespace std;
long long m,n,mod;
ll quick(ll x,int y){//快速幂
ll res=1;
while(y){
if(y&1)res=(ll)res*x%mod;
x=(ll)x*x%mod; y>>=1;
}return res;
}
int main(){
cin>>m>>n>>mod;
cout<<m<<"^"<<n<<" mod "<<mod<<"="<<quick(m,n)%mod;
}
或者你也可以这么写,下面是我早期写的版本
#include<iostream>
using namespace std;
long long b,p,k;
long long mod(long long x)
{
if(x==0) return 1%k;
long long y=x,s;
bool bo=y%2;
y/=2; s=mod(y); s*=s%k;
if(bo==1) s*=b;
return s%k;
}
int main(){
cin>>b>>p>>k;
cout<<b<<"^"<<p<<" mod "<<k<<"="<<mod(p);
}
三分法
#include<bits/stdc++.h>
#define eps 1e-6
using namespace std;
int n;
double l,r,a[20];
double f(double x){//秦九昭定理
double s=0;
for(int i=1;i<=n+1;i++)s=s*x+a[i];//巧妙的操作
return s;
}
int main(){
cin>>n>>l>>r;
for(int i=1;i<=n+1;i++)cin>>a[i];//特别注意有n+1个值
while(r-l>=eps){
double k=(r-l)/3.0;
double mid1=l+k,mid2=r-k;
if(f(mid1)>f(mid2))r=mid2;
else l=mid1;
}
printf("%.5lf",l);
}
矩阵快速幂
#include <bits/stdc++.h>
#define ll long long
#define m 1000000007
using namespace std;
inline ll gi(){
register char ch=getchar();register ll x=0;
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
ll n,k;
struct node {
ll mat[100][100];
}add,a,ans,mu,e,qk;
inline node mul(node x,node y){
node mem=qk;
for(register int i=1;i<=n;i++){
for(register int j=1;j<=n;j++){
for(register int h=1;h<=n;h++){
mem.mat[i][j]=(mem.mat[i][j]+x.mat[i][h]*y.mat[h][j])%m;//记得加上原来的
}
}
}
return mem;
}
inline void quick(ll k){
ans=e;
while(k){
if(k&1)ans=mul(ans,mu);
mu=mul(mu,mu);
k>>=1;
}
}
int main(){
cin>>n>>k;
for(register int i=1;i<=n;i++){
for(register int j=1;j<=n;j++){
mu.mat[i][j]=a.mat[i][j]=gi();
}
}
for(ll i=1;i<=n;i++){
e.mat[i][i]=1;
}
quick(k);
for(register int i=1;i<=n;i++){
for(register int j=1;j<=n;j++){
printf("%lld ",ans.mat[i][j]);
}
printf("\n");
}
return 0;
}
乘法逆元1
//法1(递推法)
#include<bits/stdc++.h>
using namespace std;
long long n,p,inv[3000001];
int main(){
cin>>n>>p;
inv[1]=1;
for(int i=2;i<=n;i++){
inv[i]=(p-p/i)*inv[p%i]%p;
}
for(int i=1;i<=n;i++)printf("%d\n",inv[i]);
}
/*递推求inv的解释:
设p=k*i+r;
则有k*i+r≡0(mod p)
为了把r^(-1)剥离出来两边同乘i^(-1)*r^(-1)
得到r^(-1)=-k*r^(-1);
k=p/i,r^(-1)=inv[p%i];
此时我们注意到这样乘起来是负数
所以我们用p减去他*/
//法2(扩展欧几里得法)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,p,inv[3000001],x,y;
void exgcd(ll a,ll b,ll &x,ll &y){
if(!b){x=1,y=0;return ;}
exgcd(b,a%b,y,x);
y-=a/b*x;
}
int main(){
cin>>n>>p;
for(int i=1;i<=n;i++){
exgcd(i,p,x,y);
x=(p+x%p)%p;
cout<<x<<endl;
}
}
/*a*x≡c(mod p)
令t=x^(-1)
我们要求的就是
x*t≡1(mod p)
于是我们有
x*t+p*y=1
求t即可*/
//法3(快速幂),即x^(p-2);
//由于这个方法只适用于x与p互质的情况,exgcd不仅比他快还适用所有情况 这里就不在赘述
乘法逆元2
//马上就考试了,这是题解,有时间补锅
#include<cstdio>
#include<cctype>
typedef long long LL;
int n,k,md,pre[5000005],suf[5000005],a[5000005];
int readint(){
int x=0;char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
inline int Inv(const int p){
if(p==1)return 1;
return((LL)(md-md/p)*Inv(md%p)%md);
}
int main(){
n=readint(),md=readint(),k=readint();
int ans=0;
for(register int i=*pre=suf[n+1]=1;i<=n;++i)
pre[i]=(LL)pre[i-1]*(a[i]=readint())%md;
for(register int i=n;i;--i)
suf[i]=(LL)suf[i+1]*a[i]%md;
for(register int i=1,j=k;i<=n;++i,j=(LL)j*k%md)
ans=(ans+(LL)j*pre[i-1]%md*suf[i+1])%md;
printf("%lld",ans*(LL)Inv(pre[n])%md);
return 0;
}
NIM游戏
#include<bits/stdc++.h>
using namespace std;
int t,n;
int main(){
cin>>t;
while(t--){
cin>>n;
int ans=0;
for(int i=1;i<=n;i++){
int ci;
cin>>ci;
ans^=ci;
}
if(ans)cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
中国剩余定理
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,a[100005],b[100005];
void exgcd(int aa,int bb,int &x,int &y){
if(!bb){x=1,y=0;return ;}
exgcd(bb,aa%bb,y,x);
y-=aa/bb*x;
}
int ksc(int aa,int bb,int mod){
int re=0;
while(bb){
if(bb&1)re=(re+aa)%mod;
bb>>=1,aa=(aa+aa)%mod;
}
return re;
}
void crt(){
int ans=0;
for(int i=1;i<=n;i++){
int mi=m/b[i],x,y;
exgcd(mi,b[i],x,y);//求出mi的逆元
ans=(ans+ksc(ksc(x,mi,m)%m,a[i],m)%m)%m;
}
ans=(ans%m+m)%m;
cout<<ans;
}
signed main(){
cin>>n;m=1;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++){cin>>b[i];a[i]=(a[i]%b[i]+b[i])%b[i];m*=b[i];}//吧a转换成正数并计算m
crt();
}
/*
对于sum{ai*mi*mi^(-1)}的解释
xi≡ai*mi*mi^(-1)(mod bi)
xj≡aj*mj*mj^(-1)(mod bj)
当循环到j时由于mj=b1*b2*...*bj-1*bj+1*...*bn
故sum之后即为答案
*/
高斯消元
#include<bits/stdc++.h>
using namespace std;
double f[4005][4005],ans[400];
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n+1;j++){
cin>>f[i][j];
}
}
for(int i=1;i<=n;i++){
int r=0;
for(int j=i;j<=n;j++)
if(fabs(f[r][i])<fabs(f[j][i]))//fabs返回实数的绝对值
r=j;
if(!r){
printf("No Solution");//找不到最大值即此列全为0
return 0;
}
swap(f[i],f[r]);//交换行骚操作~~~
double chu=f[i][i];//就是此列最大的那个关键元,那整列被放到第i行
for(int j=i;j<=n+1;j++)f[i][j]/=chu;//是i~n+1!,第1~i为0,本行除以这个关键元
for(int j=i+1;j<=n;j++){//枚举行数
chu=f[j][i];//当前行的关键元,要消去,且必须用中间变量(不然在后面的for里面值会被修改)
for(int k=i;k<=n+1;k++){//枚举列数,是i~n+1
f[j][k]-=f[i][k]*chu;//f[i][k]为这一列第一个,用关键元所在行对应列的来消此列其他值
// if(f[j][k]==-0)f[j][k]=0;
}
}
}
ans[n]=f[n][n+1];//因为是阶梯型矩阵,最后一行的第n+1个数就是xn的值
for(int i=n;i>=1;i--){//倒着枚举!
ans[i]=f[i][n+1];//本行结果初始化为第n+1个数
for(int j=i+1;j<=n;j++){
ans[i]-=ans[j]*f[i][j];//ans[j]中已经存放了xj的答案,乘本行第j个再减去就是xi的值
}
}
for(int i=1;i<=n;i++)
printf("%.2lf\n",ans[i]);
}
康托展开
//这是题解,有时间再补锅
#include <iostream>
#include <cstdio>
#define MOD (998244353)
using namespace std;
int n,a[1000000];
int c[1000001]={};
inline int lowbit(int x){
return x&(-x);
}
inline void modify(int p){
while(p<=n){
++c[p];
p+=lowbit(p);
}
return;
}
inline int ask(int p){
int s=0;
while(p){
s+=c[p];
p-=lowbit(p);
}
return s;
}
inline void readInt(int &x){
char c;
while((c=getchar())<'0' || c>'9');
x=(c^48);
while('0'<=(c=getchar()) && c<='9'){
x=x*10+(c^48);
}
return;
}
int fac[1000000]={1,1};
int main(){
int i,s=0;
readInt(n);
for(i=0;i<n;++i){
readInt(a[i]);
}
for(i=2;i<1000000;++i){
fac[i]=(long long)fac[i-1]*i%MOD;
}
for(i=0;i<n;++i){
s=(s+(long long)fac[n-1-i]*(a[i]-1-ask(a[i]-1))%MOD)%MOD;
modify(a[i]);
}
printf("%d\n",(s+1)%MOD);
return 0;
}
欧拉定理
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
using namespace std;
int n,mod,phi,k;
bool bo;
int quick(int a,int b){
int res=a,ans=1;
while(b){
if(b&1)ans=(long long)ans*res%mod;//要加ll...
res=(long long)res*res%mod;
b>>=1;
}
return ans%mod;
}
int main(){
cin>>n>>mod;
n%=mod;
int x=phi=mod;//等于mod...
for(int i=2;i*i<=x;i++){
if(x%i==0){
phi=phi/i*(i-1);
while(x%i==0)x/=i;
}
}if(x>1){phi=phi/x*(x-1);}
char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9'){
k=(k<<1)+(k<<3)+(ch^48);
ch=getchar();
if(k>=phi)bo=1,k%=phi;//>=&&%phi...
}
if(k>=phi)bo=1,k%=phi;
if(bo)k+=phi;
printf("%d",quick(n,k));
}
Pollard-Rho算法
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll ans=1;
inline ll quick(ll x,ll p,ll mod){
ll ans=1;
while(p){
if(p&1)ans=ans*x%mod;
x=x*x%mod; p>>=1;
}
return ans;
}
inline bool mr(ll x,ll p){
if(quick(x,p-1,p)!=1)return 0;
ll y=p-1,z;
while(!(y&1)){
y>>=1; z=quick(x,y,p);
if(z!=1&&z!=p-1)return 0;
return 1;
}return 1;
}
inline bool prime(ll p){ if(p<2)return 0;
if(p==2||p==3||p==5||p==11||p==101)return 1;
return mr(2,p)&&mr(3,p)&&mr(5,p)&&mr(11,p)&&mr(101,p);
}
inline ll Abs(ll x){return x<0?-x:x;}
inline ll gcd (ll a,ll b){
register ll t;
while (b){
t=a%b;
a=b;
b=t;
}
return a;
}
inline ll rho(ll p){
ll x,y,z,c,g; int i,j;
while(1){
x=y=rand()%p; c=rand()%p;
z=1; i=0; j=1;
while(++i){
x=((__int128)x*x+c)%p;
z=(__int128)z*Abs(y-x)%p;
if(x==y)break;
if(z==0){
g=gcd(Abs(y-x),p);
if(g>1)return g;
break;
}
if(!(i%127)||i==j){
g=gcd(z,p);
if(g>1)return g;
if(i==j)y=x,j<<=2;
}
}
}
}
inline void find(ll x){
if(x<=ans)return ;
if(prime(x)){ans=x;return ;}
ll p=rho(x);
while(x%p==0)x/=p;
find(p); find(x);
}
int main(){
int t;cin>>t;
srand(time(0));
while(t--){
ll n; ans=1;
cin>>n; find(n);
if(ans==n){puts("Prime");continue;}
printf("%lld\n",ans);
}
}
图类
Dij

图片备用地址:https://cdn.luogu.com.cn/upload/image_hosting/qc4lnset.png
//dij算法的负责度十分优秀,甚至可以用于含有正环的图
//但却对于含有负权边的图束手无策,因为每个点仅遍历一遍
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
int n,m,s,ji,head[1000000],dis[1000000];
bool si[100000];
priority_queue < pair < int , int > > dui;//使用堆优先更新权值最小的边,这样更有可能找到最短路
struct node{
int to,w,next;
}ed[1000000];
void ad(int p,int q,int quan){
ed[++ji].w=quan;
ed[ji].to=q;//去往哪个点
ed[ji].next=head[p];//next记录p点(该边的起点)还有连有哪些边
head[p]=ji;//head记录当前最后一条连着p点的边
}
void dij(){
for(int i=1;i<=n;i++)dis[i]=0x7fffffff;
dui.push(make_pair(0,s));
dis[s]=0;
int now,su,ne;
while(dui.size()){
now=dui.top().second;
dui.pop();
if(si[now])continue;//这个点只需更新一次
si[now]=1;
for(int i=head[now];i;i=ed[i].next){
ne=ed[i].to,su=dis[now]+ed[i].w;
if(dis[ne]>su){//更新最小值
dis[ne]=su;
dui.push(make_pair(-su,ne));//stl的堆是最大堆
}
}
}
}
int main(){
cin>>n>>m>>s;
int cu,cv,cw;
for(int i=1;i<=m;i++){
cin>>cu>>cv>>cw;
ad(cu,cv,cw);
}
dij();
for(int i=1;i<=n;i++)cout<<dis[i]<<" ";
}
spfa
//spfa算法可以弥补dij不能应对负权边及负权回路的问题,但是在毒瘤数据面前复杂度会退化
//spfa是队列优化版的Bellman-Ford,算法大致流程是用一个队列来进行维护。
//初始时将源加入队列。 每次从队列中取出一个元素,并对所有与他相邻的点进行松弛
//若某个相邻的点松弛成功,则将其入队。 直到队列为空时算法结束。
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
int n,m,s,ji,head[1000000],dis[1000000];
bool si[100000];
queue<int>dui;
struct node{
int to,w,next;
}ed[1000000];
void ad(int p,int q,int quan){
ed[++ji].w=quan;
ed[ji].to=q;
ed[ji].next=head[p];
head[p]=ji;
}
void spfa(){
for(int i=1;i<=n;i++)dis[i]=0x7fffffff;
dui.push(s);si[s]=1;dis[s]=0;
//在spfa算法中,si标记数组的作用变成了标记该点是否存在于队列中
int now,su,ne;
while(dui.size()){
now=dui.front();dui.pop();
si[now]=0;
for(int i=head[now];i;i=ed[i].next){
ne=ed[i].to,su=dis[now]+ed[i].w;
if(dis[ne]>su){
dis[ne]=su;
if(!si[ne]){
si[ne]=1;
dui.push(ne);
}
}
}
}
}
int main(){
cin>>n>>m>>s;
int cu,cv,cw;
for(int i=1;i<=m;i++){
cin>>cu>>cv>>cw;
ad(cu,cv,cw);
}
spfa();
for(int i=1;i<=n;i++)cout<<dis[i]<<" ";
}
Floyd
//Floyd算法最大的有点是面对稠密图比以上两种算法更优,而且它能求所有点互相的最短路,边权可正可负
//但三重循环也限制了它只能用于小规模数据,且不能有负权回路
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
int n,m,s,ji,dis[10000][10005];
void floyd(){
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(dis[i][k]==0x7fffffff||dis[k][j]==0x7fffffff)continue;//避免两数相加超过int范围
if(dis[i][j]>dis[i][k]+dis[k][j])dis[i][j]=dis[i][k]+dis[k][j];
}
}
}
}
int main(){
cin>>n>>m>>s;
int cu,cv,cw;
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)dis[i][j]=0x7fffffff;
for(int i=1;i<=n;i++)dis[i][i]=0;
for(int i=1;i<=m;i++){
cin>>cu>>cv>>cw;
dis[cu][cv]=min(dis[cu][cv],cw);
}
floyd();
for(int i=1;i<=n;i++)cout<<dis[s][i]<<" ";
}
负环
#include<bits/stdc++.h>
using namespace std;
int tt,n,m,head[100005],ji,dis[100005],cnt[100005];
int read(){
int x=0,f=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
while(c<='9'&&c>='0'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
struct node{
int next,yuan,w;
}ed[1000005];
void add(int p,int q,int quan){
ed[++ji].next=head[p];
ed[ji].yuan=q;
ed[ji].w=quan;
head[p]=ji;
}
bool huan;
queue<int>dui;//队列就行了
void spfa(){
while(dui.size())dui.pop();
dui.push(1);
dis[1]=0;//0号节点到根节点的距离为0
while(dui.size()){
int x=dui.front();dui.pop();
for(int i=head[x];i;i=ed[i].next){
int y=ed[i].yuan,l=dis[x]+ed[i].w;
if(dis[y]>l){
dis[y]=l;
++cnt[y];
dui.push(y);
if(cnt[y]>=n){huan=1;return;}//>=n!!!
}
}
}
}
int main(){
cin>>tt;
while(tt--){
cin>>n>>m;
memset(head,0,sizeof(head));
memset(ed,0,sizeof(ed));
memset(dis,127,sizeof(dis));
memset(cnt,0,sizeof(cnt));
ji=0,huan=0;
for(int i=1;i<=m;i++){
register int cn=read(),cm=read(),cw=read();
if(cw<0)add(cn,cm,cw);
else add(cm,cn,cw),add(cn,cm,cw);
}
spfa();
if(huan)cout<<"YE5"<<endl;
else cout<<"N0"<<endl;
}
return 0;
}
并查集
#include<bits/stdc++.h>
using namespace std;
int n,m,fa[200005];
int find(int k){
while(fa[k]!=k)k=fa[k]=fa[fa[k]];//循环版找爸爸
return k;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++){
int cn,cm,cz;
cin>>cn>>cm>>cz;
int a=find(cm),b=find(cz);
if(cn==1){
if(a>b)fa[a]=b;//按序号大小合并
else fa[b]=a;
}else{
if(a==b)cout<<"Y"<<endl;
else cout<<"N"<<endl;
}
}
}
Prime
//两者区别:Prim在稠密图中比Kruskal优,在稀疏图中比Kruskal劣。Prim是以更新过的节点的连边找最小值,Kruskal是直接将边排序。(摘自某谷Nemlit大佬)
#include<iostream>
#include<cstdio>
using namespace std;
int n,m,dis[2000000],head[2000000],ji,ans;
bool si[2000000];
struct node{
int to,next,w;
}ed[2000000];
void add(int p,int q,int quan){
ed[++ji].w=quan;
ed[ji].to=q;
ed[ji].next=head[p];
head[p]=ji;
}
void prime(){
for(int i=2;i<=n;i++)dis[i]=666666666;
for(int i=head[1];i;i=ed[i].next)dis[ed[i].to]=min(dis[ed[i].to],ed[i].w);//更新第一个点到周围点的距离
int now=1,le=n-1,lo;
while(le--){//树的边数为点数减一
si[now]=1;
lo=666666666;
for(int i=1;i<=n;i++)//找最小的边连上
if(!si[i]&&lo>dis[i]){
lo=min(lo,dis[i]);
now=i;
}
ans+=lo;
for(int i=head[now];i;i=ed[i].next){//更新跟目前节点相连各店的距离
if(!si[ed[i].to])dis[ed[i].to]=min(dis[ed[i].to],ed[i].w);
}
}
}
int main(){
cin>>n>>m;
int cn,cm,cw;
for(int i=1;i<=m;i++){
cin>>cn>>cm>>cw;
add(cn,cm,cw);//无向图则双向建边
add(cm,cn,cw);
}
prime();
if(ans<666666666)cout<<ans;
else cout<<"orz";
}
Kruskal
#include<bits/stdc++.h>
using namespace std;
struct tree{
int to,next,w;
}ed[2000005],Ed[2000005];
int m,ji,n,head[2000005],ans,fa[2000005];
bool cmp(tree a,tree b){//比较函数
return a.w<b.w;
}
int find(int k){//循环版找爸爸
while(k!=fa[k])k=fa[k]=fa[fa[k]];
return k;
}
void kruskal(){
sort(ed+1,ed+m+1,cmp);
for(int i=1;i<=m;i++){
int x=find(ed[i].next),y=find(ed[i].to);
if(x==y)continue;
if(x>y){
fa[y]=x;
}
else
fa[x]=y;
ans+=ed[i].w;
if(++ji==n-1)return ;
}
}
bool tong[2000005];//标记是否连通
void dfs(int now){
tong[now]=1;
for(int i=head[now];i;i=Ed[i].next){
if(!tong[Ed[i].to])dfs(Ed[i].to);
}
}
void add(int p,int q,int quan){
Ed[++ji].w=quan;
Ed[ji].to=q;
Ed[ji].next=head[p];
head[p]=ji;
}
int main(){
cin>>n>>m;
int cn,cm,cw;
for(int i=1;i<=m;i++){
cin>>cn>>cm>>cw;
ed[i].next=cn,ed[i].to=cm,ed[i].w=cw;
add(cn,cm,cw);
add(cm,cn,cw);
}
dfs(1);
ji=0;
for(int i=1;i<=n;i++)if(!tong[i]){cout<<"orz";return 0;}//某谷最新数据要求判断是否连通
for(int i=1;i<=n;i++)fa[i]=i;
kruskal();
cout<<ans;
}
tarjan
//推荐 https://blog.csdn.net/qq_34374664/article/details/77488976
//[USACO06JAN]The Cow Prom S
#include<iostream>
#include<stack>
using namespace std;
int n,m,ji,head[1000000],dfn[1000000],low[1000000],ans;
bool bo[1000000];
struct node{
int to,next;
}ed[1000000];
void add(int p,int q){
ed[++ji].to=q;
ed[ji].next=head[p];
head[p]=ji;
}
stack<int> dui;
void tar(int k){
dfn[k]=low[k]=++ji;//我对dfn的理解是第几个被访问的
//low就是这个强连通分量里最先被访问的节点的dfn
bo[k]=1;//在栈里面
dui.push(k);
for(int i=head[k];i;i=ed[i].next){
if(!dfn[ed[i].to]){//能拓展节点
tar(ed[i].to);
low[k]=min(low[k],low[ed[i].to]);
}else if(bo[ed[i].to])//在栈里
low[k]=min(low[k],low[ed[i].to]);
}
if(low[k]==dfn[k]){
int mem=1;//k节点自身也是一个强连通分量
while(dui.top()!=k&&dui.size()){
bo[dui.top()]=0;
dui.pop();
mem++;
}
dui.pop();
bo[k]=0;
if(mem>1)++ans;//题目要求数个数大于一的
}
}
int main(){
cin>>n>>m;
int cn,cm;
for(int i=1;i<=m;i++){
cin>>cn>>cm;
add(cn,cm);
}
ji=0;
for(int i=1;i<=n;i++){
if(!dfn[i])tar(i);//防止有森林出现漏掉其他树
}
cout<<ans;
}
缩点
//SCC是强连通分量
#include<iostream>
#include<stack>
#include<queue>
using namespace std;
int n,m,ji,jied,head[1000000],headEd[1000000],w[1000000],dfn[1000000],low[1000000],sum[1000000],mem[1000000][3];
int read(){
int x=0;char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch<='9'&&ch>='0')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
struct node{
int to,next;
}ed[1000000],Ed[1000000];
void add(int p,int q){
ed[++ji].to=q;
ed[ji].next=head[p];
head[p]=ji;
}
bool bo[1000000];
stack<int> sta;
queue<int>dui;
int scc[1000000],col,in[1000000],dis[1000000];
void tarjan(int k){
dfn[k]=low[k]=++ji;
bo[k]=1;sta.push(k);
for(int i=head[k];i;i=ed[i].next){
if(!dfn[ed[i].to]){
tarjan(ed[i].to);
low[k]=min(low[k],low[ed[i].to]);
}else{
if(bo[ed[i].to])
low[k]=min(low[k],low[ed[i].to]);
}
}
if(dfn[k]==low[k]){
++col;bo[k]=0;//打上颜色标记,表示在一个SCC内
while(sta.top()!=k&&sta.size()){
scc[sta.top()]=col;
sum[col]+=w[sta.top()];//sum记录SCC内的点权之和
bo[sta.top()]=0;
sta.pop();
}
sta.pop();
scc[k]=col,sum[col]+=w[k];
}
}
void addEd(int p,int q){
Ed[++ji].to=q;
Ed[ji].next=headEd[p];
headEd[p]=ji;
}
void topo(){
for(int i=1;i<=col;i++)dis[i]=sum[i];//这样赋值是防止孤立的SCC不被考虑
while(dui.size()){
int x=dui.front();
dui.pop();
for(int i=headEd[x];i;i=Ed[i].next){//以每一个根为起点进行松弛
int y=Ed[i].to;
--in[y];
dis[y]=max(dis[y],dis[x]+sum[y]);
if(!in[y])dui.push(y);//?????
}
}
}
int main(){
n=read(),m=read();
int cn,cm;
for(int i=1;i<=n;i++){
w[i]=read();
}
for(int i=1;i<=m;i++){
cn=read(),cm=read();
add(cn,cm);
mem[i][1]=cn,mem[i][2]=cm//记录每条有向边的起点和终点
}
ji=0;
for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i);
ji=0;
for(int i=1;i<=m;i++){
if(scc[mem[i][1]]!=scc[mem[i][2]]){
addEd(scc[mem[i][1]],scc[mem[i][2]]);//注意是以每个scc为点建边
in[scc[mem[i][2]]]++;//记录每个点的入度
}
}
//缩点到此结束,题目要求找一条最长路
for(int i=1;i<=n;i++)if(!in[i])dui.push(i);//没有入度的点是孤立的点(森林)
topo();
int ans=0;
for(int i=1;i<=n;i++){
ans=max(ans,dis[i]);
}
cout<<ans;
}
LCA
#include<bits/stdc++.h>
using namespace std;
int n,m,root,f[500005][25];
struct node{
int next,yuan;
}ed[5000005];
int head[500005],ji,de[500005];
inline int read(){
register int x=0;char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
inline void add(int p,int q){
ed[++ji].next=head[p];
ed[ji].yuan=q;
head[p]=ji;
}
inline void dfs(int k,int ste){
for(int j=1;j<=20;j++){//因为不一定编号小的就是编号大的 的祖先所以要在dfs时预处理f
f[k][j]=f[f[k][j-1]][j-1]; //还有,f预处理必须放在dfs前面,因为后面的儿子会要用到这个f
}
for(register int i=head[k];i;i=ed[i].next){
register int y=ed[i].yuan;
if(!de[y]){
de[y]=ste;
f[y][0]=k;
dfs(y,ste+1);
}
}
}
inline int lca(int p,int q){
if(de[p]>de[q])swap(p,q);
for(register int i=20;i>=0;i--){
if(de[f[q][i]]>=de[p])q=f[q][i];//记得是>=!!!
}
if(p==q)return p;
for(register int i=20;i>=0;i--){
if(f[p][i]!=f[q][i]){
p=f[p][i],q=f[q][i];
}
}
return f[p][0];
}
int main(){
cin>>n>>m>>root;
for(register int i=1;i<n;i++){
register int cn=read(),cm=read();
add(cn,cm);add(cm,cn);
}
de[root]=1;
dfs(root,2);
for(register int i=1;i<=m;i++){
register int cn=read(),cm=read();
printf("%d\n",lca(cn,cm));//cout->printf 2.7s->1.7s
}
}
分层图
//然而放的并不是分层图的做法,放的是Dij或spfa+DP的做法,貌似比正解还快???
//首先是Dij版的
#include<bits/stdc++.h>
using namespace std;
int n,m,k,f[100005][30];
int read(){
int x=0;char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
int head[1000005],ji;
struct node{
int next,yuan,w;
}ed[1000005];
void add(int p,int q,int quan){
ed[++ji].next=head[p];
ed[ji].yuan=q;
ed[ji].w=quan;
head[p]=ji;
}
struct no{
int dis,x,now;
bool operator > (const no& bb)const{return dis<bb.dis;}
bool operator < (const no& bb)const{return dis>bb.dis;}//重中之重,重载运算符(直接变成小跟堆)
};
priority_queue< no >dui;
bool bo[100005][30];
void dij(){
memset(f,127,sizeof(f));
f[1][0]=0;
dui.push(no{0,1,0});
while(dui.size()){
int x=dui.top().x,now=dui.top().now;
dui.pop();
if(bo[x][now])continue;
bo[x][now]=1;
for(int i=head[x];i;i=ed[i].next){
int y=ed[i].yuan;
if((!bo[y][now])&&f[y][now]>f[x][now]+ed[i].w){
f[y][now]=f[x][now]+ed[i].w;
dui.push(no{f[y][now],y,now});
}
if((!bo[y][now+1])&&now<k&&f[y][now+1]>f[x][now]){
f[y][now+1]=f[x][now];
dui.push(no{f[y][now+1],y,now+1});
}
}
}
}
int main(){
n=read(),m=read(),k=read();
for(int i=1;i<=m;i++){
int cn=read(),cm=read(),cw=read();
add(cn,cm,cw);
add(cm,cn,cw);
}
dij();
cout<<f[n][k]<<endl;
return 0;
}
//法二,spfa版(当然比Dij慢多了)
#include<bits/stdc++.h>
using namespace std;
int n,m,k,f[100005][30];
int read(){
int x=0;char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
int head[1000005],ji;
struct node{
int next,yuan,w;
}ed[1000005];
void add(int p,int q,int quan){
ed[++ji].next=head[p];
ed[ji].yuan=q;
ed[ji].w=quan;
head[p]=ji;
}
queue<pair<int,int> >dui;
bool bo[100005][30];
void spfa(){
memset(f,127,sizeof(f));
dui.push(make_pair(1,0));
bo[1][0]=1,f[1][0]=0;
while(dui.size()){
int x=dui.front().first,now=dui.front().second;
dui.pop();
bo[x][now]=0;
for(int i=head[x];i;i=ed[i].next){
int y=ed[i].yuan;
if(f[y][now]>f[x][now]+ed[i].w){
f[y][now]=f[x][now]+ed[i].w;
if(!bo[y][now]){
bo[y][now]=1;
dui.push(make_pair(y,now));
}
}
if(now<k&&f[y][now+1]>f[x][now]){
f[y][now+1]=f[x][now];
if(!bo[y][now+1]){
bo[y][now+1]=1;
dui.push(make_pair(y,now+1));
}
}
}
}
}
int main(){
n=read(),m=read(),k=read();
for(int i=1;i<=m;i++){
int cn=read(),cm=read(),cw=read();
add(cn,cm,cw);
add(cm,cn,cw);
}
spfa();
int ans=0x7fffffff;
for(int i=0;i<=k;i++)ans=min(ans,f[n][i]);
cout<<ans<<endl;
return 0;
}
树上启发式合并(配重链剖分)
#include<iostream>
#include<set>
using namespace std;
struct node {
int next,to;
}t[200005];
int ji, head[200005];
int n, ans = 0 ;
int tree_size[200005], le[200005], ri[200005], id = 0, son_list[200005], son[200005], cnt[200005], col[200005];
multiset<int> s;
void add(int p,int q) {
t[++ji].to = q;
t[ji].next = head[p];
head[p] = ji;
}
void cal_son(int now,int fa) {
tree_size[now] = 1;
le[now] = ++id;
son_list[id] = now;
for (int i = head[now]; i; i = t[i].next) {
int next = t[i].to;
cal_son(next,now);
tree_size[now] += tree_size[next];
if (!son[now] || tree_size[next] > tree_size[son[now]])son[now] = next;//son选size最大的
}
ri[now] = id;//le和ri记录以now为父亲的子树的所有结点在son_list中的下标
}
void cal_col(int now_col,int k) {
if (cnt[now_col])s.erase(s.find(cnt[now_col]));//要find,否则相同值会全部删掉
cnt[now_col] += k;
if (cnt[now_col])s.insert(cnt[now_col]);
}
int check() {
int first = *s.begin();
int end = *(--s.end());
return first == end;//集合自动排序,头=尾则说明最大值等于最小值
}
void dfs(int now,int fa,int del) {
for (int i = head[now]; i; i = t[i].next) {
int next = t[i].to;
if (next==fa || son[now] == next)continue;
dfs(next, now, 1);//del=1表示轻儿子,统计答案后要删除
}
if (son[now])dfs(son[now], now, 0);
for (int i = head[now]; i; i = t[i].next) {
int next = t[i].to;
if (next == fa || son[now] == next)continue;
for (int j = le[next]; j <= ri[next]; j++) {//统计轻儿子下面所有的点的答案
cal_col(col[son_list[j]], 1);
}
}
cal_col(col[now],1);//统计now
if (check())ans++;
if (del) {
for (int i = le[now]; i <= ri[now]; i++) {
cal_col(col[son_list[i]], -1);//删除
}
}
}
int main() {
cin >> n;
int cm;
for (int i = 1; i <= n; i++) {
cin >> col[i];
cin >> cm;
add(cm, i);
}
cal_son(1, 0);
dfs(1, 0, 0);
cout << ans << endl;
}
STL类
堆
#include<bits/stdc++.h>
using namespace std;
int n;
priority_queue<int,vector<int>,greater<int> >dui;
int main(){
cin>>n;
for(register int i=1;i<=n;++i){
register int ty;cin>>ty;
if(ty==1){
cin>>ty;
dui.push(ty);
}
else if(ty==2){
cout<<dui.top()<<endl;
}else{
dui.pop();
}
}
}
字符串类
manacher
//注意此算法求的是回文串,必须是连续的一段序列
//而回文序列则不必连续
#include<bits/stdc++.h>
using namespace std;
char s[31000005];
int r[31000005],len;//r是包括自己向右扩展的最大半径
int main(){
s[0]=s[1]='#';len=2;
while(cin>>s[len]){
s[++len]='#';++len;
}
--len;//在每个字符之间插板子
r[0]=r[1]=r[2]=1;
int maxr=2,pos=0,ans=0;
for(int i=3;i<=len;i++){//必须一个一个更新 因为可能答案是关于‘#’对称的。。。
if(i<maxr){
r[i]=min(r[(pos<<1)-i],maxr-i);//两种情况
}else r[i]=1;
for(;s[i-r[i]]==s[i+r[i]];++r[i]);//左右拓展
if(maxr<i+r[i])pos=i,maxr=i+r[i];
ans=max(ans,r[i]);
}
cout<<ans-1;//半径减去‘#’的个数
}
KMP
#include<bits/stdc++.h>
using namespace std;
int n,m,lena,lenb,nex[1000005];
char a[1000005],b[1000005];
int main(){
scanf("%s%s",a+1,b+1);
lena=strlen(a+1);
lenb=strlen(b+1);
int j=0;
for(int i=2;i<=lenb;i++){
while(j&&b[i]!=b[j+1])j=nex[j];
if(b[i]==b[j+1])++j;
nex[i]=j;
}
j=0;
for(int i=1;i<=lena;i++){
while(j&&b[j+1]!=a[i])j=nex[j];
if(b[j+1]==a[i])++j;
if(j==lenb){cout<<i-lenb+1<<endl;j=nex[j];}
}
for(int i=1;i<=lenb;i++)cout<<nex[i]<<" ";
return 0;
}
字符串hash
#include<bits/stdc++.h>
#define ull unsigned long long
using namespace std;
ull n,a[100005];
char s[100005];
ull mod=20190816170251;
ull base=131;
ull ha(int len){
ull ans=0;
for(int i=0;i<len;i++){
ans=(ans*base+(ull)s[i])%mod+19260817;//别问为什么是这个数,问就禁言
}
return ans;
}
int main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++){
scanf("%s",s);
a[i]=ha(strlen(s));
}
int ans=1;
sort(a+1,a+n+1);
for(int i=1;i<n;i++){
if(a[i]!=a[i+1])
ans++;
}
printf("%d",ans);
}
/*字符串hash的原理:
比如abcde,则
ha[1]=a,ha[2]=ab,ha[3]=abc,ha[4]=abcd,ha[5]=abcde
倒过来hash:
ha[1]=e,ha[2]=ed,ha[3]=edc,ha[4]=edcb,ha[5]=edcba
所以如果要取出'cba'的子串
则要用ha[5]-ha[2]*(base^(5-2)) */
高精度
高精度加法
#include<iostream>
#include<cstring>
#include<cstdio>
#define maxn 1000000
using namespace std;
char d[maxn],e[maxn];
int a[maxn],b[maxn],c[maxn];
int main(){
scanf("%s%s",&d,&e);
int lena=strlen(d),lenb=strlen(e),lenc=lena>lenb?lena:lenb,jin=0;
for(int i=0;i<lena;i++){
a[lena-i]=d[i]-48;
}
for(int i=0;i<lenb;i++){
b[lenb-i]=e[i]-48;
}
for(int i=1;i<=lenc;i++){
c[i]=a[i]+b[i]+jin;
jin=c[i]/10;
c[i]%=10;
}
lenc++;
c[lenc]=jin;
while(!c[lenc]&&lenc>1){
lenc--;
}
for(int i=lenc;i>=1;i--)printf("%d ",c[i]);
return 0;
}
高精度减法
#include<iostream>
#include<cstdlib>
#include<cstring>
using namespace std;
int a[1000000],b[1000000],c[1000000];
char d[1000000],e[1000000];
bool mi;
int main(){
scanf("%s%s",&d,&e);
if(!strcmp(d,e)){cout<<"0";return 0;}//特判是否相同
int lena=strlen(d),lenb=strlen(e);
for(int i=0;i<lena;i++)a[lena-i]=d[i]-48;
for(int i=0;i<lenb;i++)b[lenb-i]=e[i]-48;
while(!a[lena])lena--;//题目中说了有前导0(没有的请忽略)
while(!b[lenb])lenb--;
int len=lena>lenb?lena:lenb;
if(((strcmp(d,e)<0)&&(lena==lenb))||(lena<lenb))
mi=1;//不用区交换数组了
if(!mi)//记得分清谁减谁
for(int i=1;i<=len;i++){
if(a[i]<b[i]){a[i]+=10;a[i+1]--;}
c[i]=a[i]-b[i];
}
else
for(int i=1;i<=len;i++){
if(b[i]<a[i]){b[i]+=10;b[i+1]--;}
c[i]=b[i]-a[i];
}
while(!c[len]&&len>1)--len;
if(mi)cout<<"-";
for(int i=len;i>=1;i--)cout<<c[i];
}
高精度乘法
#include<iostream>
#include<cstring>
using namespace std;
int a[2005],b[2005],c[2005];
char a1[2005],b1[2005];
int main(){
scanf("%s%s",&a1,&b1);
int lena=strlen(a1),lenb=strlen(b1);
for(int i=0;i<lena;i++) a[lena-i]=a1[i]-'0';
for(int i=0;i<lenb;i++) b[lenb-i]=b1[i]-'0';
for(int i=1;i<=lenb;i++){
int jin=0;
for(int j=1;j<=lena;j++){
c[i+j-1]=a[j]*b[i]+jin+c[i+j-1];
jin=c[i+j-1]/10;
c[i+j-1]%=10;
}
c[lena+i]=jin;
}
int lenc=lena+lenb;
while(!c[lenc]&&lenc>1)lenc--;
for(int i=lenc;i>=1;i--)printf("%d ",c[i]);
return 0;
}
高精除以低精(附带出输出余数)
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int a[2005],b,c[2005],jin;
char a1[2005];
int main(){
scanf("%s",&a1);
cin>>b;
int lena=strlen(a1);
for(int i=0;i<lena;i++) a[i+1]=a1[i]-'0';//记得是从前往后处理
for(int i=1;i<=lena;i++){
c[i]=(jin*10+a[i])/b;
jin=(jin*10+a[i])%b;
}
int lenc=1;
while(!c[lenc]&&lenc<lena)lenc++;
for(int i=lenc;i<=lena;i++)printf("%d",c[i]);
cout<<endl<<jin;
return 0;
}
//jin取的是前面的余数,把前面的余数拼到后面一起除
排序
安利 https://blog.csdn.net/songjiasheng1314/article/details/80663744
选择排序
//选择排序的核心思想是找到一个最小的元素(第二层循环中ji就是最小元素在无序数组中的编号)然后把它放到最前面
#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
int a[99999999],n;
void swap(int &l,int &k){
int t=l;
l=k;
k=t;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=n;i++){
int ji=i;
for(int j=i+1;j<=n;j++){
if(a[j]<a[ji])ji=j;
}
if(ji!=i)swap(a[i],a[ji]);//要传址调用
}
cout<<endl;
for(int i=1;i<=n;i++)
printf("%d ",a[i]);
return 0;
}
正版冒泡
//冒泡排序的核心思想是一遍一遍地比较相邻两个数并交换顺序
#include<iostream>
#include<cstdio>
using namespace std;
int a[99999999],n;
int main(){
cin>>n;
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=n-1;i>=1;i--){
for(int j=0;j<=i;j++){
if(a[j]>a[j+1]) swap(a[j],a[j+1]);
}
}
for(int i=1;i<=n;i++)printf("%d ",a[i]);
return 0;
}
盗版冒泡
#include<iostream>
#include<cstdio>
using namespace std;
int a[99999999],n;
int main(){
cin>>n;
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
if(a[i]>a[j]) swap(a[i],a[j]);
}
}
for(int i=1;i<=n;i++)printf("%d ",a[i]);
return 0;
}
插排
//顾名思义
#include<iostream>
#include<cstdio>
using namespace std;
int a[99999999],n,i,j;
void yi(int p,int q){
for(int h=q;h>p;h--)a[h]=a[h-1];
}
int main(){
cin>>n;
for( i=1;i<=n;i++)scanf("%d",&a[i]);
for( i=2;i<=n;i++){//a[i]为需要插入的数
for( j=i-1;j>=1;j--)//寻找插入点
if(a[j]<a[i])break;
if(j!=i-1){//需要将a[i]插入a[j]后
int temp=a[i];
yi(j+1,i);
a[j+1]=temp;
}
}
for(i=1;i<=n;i++)printf("%d ",a[i]);
return 0;
}
桶排
//开一个数组记录所有数字出现了几次,最后按数组顺序输出
#include<iostream>
#include<cstdio>
using namespace std;
int a[99999999],n,ji;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
scanf("%d",&ji);
a[ji]++;
}
for(int i=0;i<=n;i++){
while(a[i]){
printf("%d ",i);
a[i]--;
}
}
return 0;
}
快速排序
#include<bits/stdc++.h>
using namespace std;
int n,a[100005];
int read(){//快读优化
int x=0;char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
void quick_sort(int l,int r){
if(l>=r)return ;
int mid=a[(l+r)>>1],i=l,j=r;//我习惯用将基准数设为中间的那个数
while(i<=j){
while(a[i]<mid)++i;//不能加‘=’,否则当mid为整个数组中的最大数时会陷入死循环
while(a[j]>mid)--j;
if(i<=j){//要特判,否则i>j了就是在帮倒忙了
swap(a[i],a[j]);
++i,--j;//不在原地踏步
}
}
if(l<j)quick_sort(l,j);//!!! 一遍快排之后i>j了所以~
if(r>i)quick_sort(i,r);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
a[i]=read();
}
quick_sort(1,n);
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
}
}
三数取中+冒泡版 快排
//
#include<iostream>
#include<cstdio>
using namespace std;
int a[99999999],n;
void cha(int p,int q){//p<q
int ji=0,j;
for(int i=p+1;i<=q;i++){
for(j=p;j<i;j++)if(a[i]<a[j])break;
ji=a[i];
for(int k=i-1;k>=j;k--)a[k+1]=a[k];//千万记得是倒序赋值
a[j]=ji;
}
}
void quick(int le,int ri){
if(le>=ri)return;
if(ri-le<=10)cha(le,ri);
int t=(le+ri)/2,mid,x=le,y=ri;//在左端点右端点和中点位置的三个数中选取大小排中间的数,并将另外两数按大小分别赋给左右端点
if(a[le]<a[t]){
if(a[t]>a[ri]){
int w=a[t];
a[t]=a[ri];a[ri]=w;
}
}
if(a[le]>a[t]){
int w=a[t];
a[t]=a[le];
a[le]=w;//a[le]<a[t]
if(a[t]>a[ri]){
int w=a[t];
a[t]=a[ri];a[ri]=w;
}
}
mid=a[t];
while(x<=y){
while(a[x]<mid)x++;
while(a[y]>mid)y--;
if(x<=y){
int w=a[x];
a[x]=a[y];a[y]=w;
x++;y--;
}
}
if(le<y)quick(le,y);
if(x<ri)quick(x,ri);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
quick(1,n);
for(int i=1;i<=n;i++)printf("%d ",a[i]);
return 0;
}
归并排序
#include<iostream>
#include<cstdio>
using namespace std;
int a[99999999],b[99999999],n;
void gui(int le,int ri)
{
if(le==ri)return;
int mid=(le+ri)/2,x=le,y=mid+1,k=le;
gui(le,mid);
gui(mid+1,ri);
while(x<=mid&&y<=ri)
if(a[x]<a[y])b[k++]=a[x++];
else b[k++]=a[y++];
while(x<=mid)b[k++]=a[x++];
while(y<=ri)b[k++]=a[y++];
for(int g=le;g<=ri;g++)a[g]=b[g];
}
int main(){
cin>>n;
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
gui(1,n);
for(int i=1;i<=n;i++)printf("%d ",a[i]);
return 0;
}
基数排序
基数排序的核心思想是按顺序(从高往低或者从低往高)比较每个数字的个位十位百位等等,每次按当前数位上的数值大小将数组重新排列,然后将新数列按下一位上的数值大小比较并再次排序,以此类推即可得到答案
#include<iostream>
#define ll long long
using namespace std;
ll ma,n,a[200000],tub[15][200000],bas[15]={1,10,100,1000,10000,100000,1000000,10000000,100000000,1000000000,10000000000,100000000000,1000000000000,10000000000000},k;
int main(){
cin>>n;
for(ll i=1;i<=n;i++){
cin>>a[i];
ll t=1;
while(a[i]>=bas[t])++t;
ma=max(ma,t);//统计有多少位
}
for(ll t=1;t<=ma;t++){
for(ll i=1;i<=n;i++){
k=(a[i]%(bas[t]))/bas[t-1];tub[k][++tub[k][0]]=a[i];//按当前位大小放入桶子里
}
ll now=1;
for(ll i=1;i<=n;i++)
for(k=0;k<=9;k++){
for(ll ji=1;ji<=tub[k][0];ji++)
a[now++]=tub[k][ji];//按桶子的顺序重新排序
tub[k][0]=0;//记录桶子里有多少个数
}
}
for(ll i=1;i<=n;i++)cout<<a[i]<<" ";
}
测试数据生成器
#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<ctime>
using namespace std;
int main(){
freopen("testdata.in","w",stdout);
srand((unsigned)time(NULL));
for(int i=1;i<=10000;i++)
printf("%d ",rand());
return 0;
}
本文版权归作者LHR,欢迎转载,但未经LHR同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则LHR保留追究法律责任的权利。

