方差(Variance)、协方差(Covariance)与相关性系数

方差
方差主要计算一维数组的离散程度

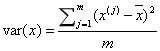
协方差
协方差主要衡量两组变量或者二维变量的相似程度


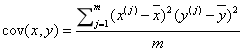
很明显，所谓的协方差就是方差在二维上的呈现。那么一维数据自身的协方差是如何计算呢？

一维数据和自己的协方差，就是数据本身的方差，方差是协方差的特殊情况。
值得注意的是当两组数据的协方差为0时，说明两组数据线性无关。而两组数据的协方差越大，相关性也就越大。当协方差为负时，两组数据负相关，反之为正相关。

相关性系数

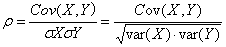
相关性系数也可以被理解成一种特殊的协方差。相对于协方差来说，它是经过了标准化的消除了变化幅度的影响的协方差，可以单纯反应两个变量每单位变化时的相似程度。
这里的消除变化幅度的影响如何理解呢？两组数据变化趋势相同时，可能幅度相差很多，导致协方差的计算值在负无穷到正无穷之间变化。但我们经过了标准化处理，使得相关性系数的值集中在-1到1之间。当相关系数为－1时，说明两个变量变化的反向相似度最大，X增大时，Y进行等值缩小，反之亦然。