Representation Learning: A Review and New Perspectives

1、 INTRODUCTION

机器学习算法的成功通常取决于数据表示，虽然特定领域的知识可以用来帮助设计表示，但也可以使用使用通用先验的学习，而对人工智能的追求正在激励人们设计更强大的表示学习算法来实现这些先验。
本文回顾了在无监督特征学习和深度学习领域的最新工作，包括概率模型、自动编码器、流形学习和深度网络的进展。这引发了关于学习良好表示的适当目标、计算表示（即推理）以及表示学习、密度估计和流形学习之间的几何联系的长期未解问题
1、当前学习算法的弱点：它们无法从数据中提取和组织鉴别信息。特征工程是一种利用人类的独创性和先验知识来弥补这一弱点的方法。为了扩大机器学习的适用范围和易适用性，最好使学习算法减少对特征工程的依赖，以便更快地构建新的应用程序，更重要的是，在人工智能（AI）方面取得进展。人工智能必须从根本上理解我们周围的世界，我们认为，只有学会识别和解开隐藏在低水平感官数据的观察环境中的潜在解释因素，才能做到这一点。
本文是关于表示学习的，即学习数据的表示，使其在构建分类器或其他预测器时更容易提取有用的信息。在各种学习表示的方法中，本文主要关注深度学习方法：那些由多个非线性变换组成的方法，目的是产生更抽象的、最终更有用的表示。在这里，我们调查了这个快速发展的领域，特别强调了最近的进展。我们考虑了推动这一领域研究的一些基本问题。具体来说，是什么使一种表现比另一种更好？举一个例子，我们应该如何计算它的表示，即执行特征提取？另外，学习好的表征的合适目标是什么？

2、表示学习应用领域

利用大量参考文献指出在下面的领域取得成果
（1） 语音识别和信号处理（2）目标识别（3）自然语言处理（4）多任务和转移学习，领域适应（寻找不同特征间的共性）

3、什么使表征变好？

3.1、人工智能中表示学习的先验

（1）平滑（2）多种解释因素（3）解释因素的分层组织（4）半监督学习（5）任务间共享因子（6）流形（7）自然聚类（8）时间和空间一致性（9）稀疏（10）简单的因素依赖 这些都可以用来帮助学习表征。
•平滑:如果x约等于y，那么f(x)约等于f(y)，其中f是要学习的的函数。这个假设允许学习器从训练样本泛化到输入空间中附近的点(f(d+e) = f(d), e is small)，但是这个假设无法克服维数灾难。
•多种解释因素：数据是由多个潜在解释因子生成的，并且给定每一个因子的状态，大多数任务都能轻易解决。
•解释因素的分层组织：高级抽象的概念能通过简单的概念层次化定义。比如，深度架构表达了我们认为任务由多个步骤完成的概念即每一步回溯到先前步骤处理之后的输出。
•半监督学习：对于输入数据X和目标Y，描述X分布的部分因子再给定X的情况下能很好的解释Y。所以对于P(x)有用的信息在学习P(Y|x)时也很有用即允许共享监督学习和非监督学习之间的统计优势。
•任务间共享因子：当多个对应到不同变量yi的任务共享相同的输入x时，或者当每个任务关联到全局输入x的子集或者函数fi(x)时，我们会假设每个变量yi关联到来自相关因素h公共池的不同子集。因为这些子集有重叠，所以通过共享的中间表示p(h|x)来学习所有的p(yi|x)能够使任务间共享统计强度。
•流形：在概率质量集中区域，可用比数据所在原始空间低得多的低维流形来近似。在一些机器学习算法中，特别使自编码器会视图显式地学习流行的结构。这里对流行做一下简单解释。流行来自于拓扑学，数学上视作一组点，每个点都有邻域。给定一个任意一个点，其流行局部看起来是欧几里得空间，可以使用欧氏距离。在流行学习中认为，我们观察到的大多数高维数据是一些低维数据在高位空间中的映射。在高维空间中数据时冗余的，大部分区域是无效输入，有意义的数据只分布在包含少数数据点的子集构成的一组流形中，有意义的变化都沿着流形的方向或者发生在切换到另一流行时。简单解释流形可以类比一张A4纸(二维的)扭曲后立起来，呈现在给人的是三维的。流形主要用于降维和特征学习。
•自然聚类：不同种类的客体类别都与不同的流形有关联。精确些就是在同一个流形中，局部的变体会保留下对应类别的信息。很多机器学习算法假设输入空间中每个联通流行可以被分配到一个单独的类中。数据在许多不连通的流形上，但相同流行上数据的类别是相同的
•时间和空间一致性：时间上连续的或者空间上邻近的信息一般对应着同一个相关的内容或者从流行角度看就是在高维流行表面移动很慢。更一般的讲，不同的因子在时间或空间上不同尺度的变化对于许多类别相关的信息影响不明显。所以在捕获类别相关变量时，根据这个知识可以考虑那些使表征变化不大的因素。
•稀疏：大部分特征和大部分输入是不相关的。呈现在表示中的化就是大部分元素为0。也就是说，与输入数据x有关的因素只有一小部分。
•简单的因素依赖：在优秀的高级表示中，因子会通过简单的线性依赖相互关联。比如一般会在学好的表示顶层加一层线性分类器。

3.2、平滑和维度的诅咒

虽然平滑可以是一个有用的假设，但它还不足以解决维度的问题，因为当数据在原始输入空间中表示时，这样的皱纹数量wrinkles(目标函数的起伏)可能随着相关的交互因子的数量呈指数增长。因此需要将平滑性条件与其他通用先验条件结合

3.3、分布式表示

良好的表示是表达性的，这意味着一个合理大小的学习表示可以捕获大量可能的输入配置
一个one-hot表示，例如传统的聚类算法、高斯混合模型。最近邻算法、高斯SVM等的结果都需要O(N)个参数来区分O(N)个输入区域。但是像RBM、sparse coding、auto-encoder或者多层神经网络可以用O(N)个参数表示O(2^k)个输入区域。它们就是分布式表示。

3.4、深度和抽象

能够促进特征重用和使用更高层的抽象特征
深度回路的一个重要性质是path的数量，它会相对于深度呈指数级增长。我们可以改变每个节点的定义来改变回路的深度。典型的计算包括：weighted,sum, product, artificial neuron model,computation of a kernel, or logic gates.Abstraction and invariance
更抽象的表示检测到涵盖更多不同现象的类别（例如，更大的流形和更多的皱纹），因此它们可能具有更大的预测能力。更抽象的概念可以依靠less抽象的概念构造。例如在CNN中，通过pooling来构造这种抽象，更抽象的概念一般是对于大部分输入的局部变化具有不变性。

3.5、解开变异因子

最鲁棒的特征学习是尽可能多的解决变异因子，抛弃尽可能少的信息，类似降维。

3.6、好的表示学习的标准

Distributed ： 分布式 包含更多的输入
Invariant： 更抽象，对输入的局部变化有不变性
Disentangle ： 分离更多因素，减小因素间的互相影响

4、构建深层表征

原因：实验发现深层表征效果好
为了学习一种好的表示，需要构建具有一定“深度”的模型，并通过学习算法来让模型自动学习出好的特征表示（从底层特征，到中层特征，再到高层特征），从而最终提升预测模型的准确率。表示学习的关键是构建具有一定深度的多层次特征表示。所谓“深度”是指原始数据进行非线性特征转换的次数，深度学习其主要目的是从数据中自动学习到有效的特征表示，通常需要从底层特征开始，经过多步非线性转换才能得到。深层结构的优点是可以增加特征的重用性，从而指数级地增加表示能力。

许多种类的只有一个隐藏层的网络都可以被视为万能的近似器。确定性前馈网络是函数的万能近似器，许多具有单个隐藏层的结构化概率模型是概率分布的万能近似器。但是在很多浅层网络例如线性网络不能学习到一些抽象解释因子和复杂的内部联系。这些解释因子很可能是高度抽象的，并且和输入呈高度非线性关系。这些因子几乎彼此独立地被抽取，但仍然对应到有意义的输入因素。因此，我们需要深度的分布式表示，需要许多非线性组合来获得较高级的特征(输入的函数)或因子(生成原因)。

借鉴于贪心逐层非监督预训练，构建深度表示的一个重要想法是学习一个特征层级，一次训练一层。在每一层使用非监督特征学习得到一个新的转化并与先前学习到的的转化组合在一起。这个非监督学习的每一次迭代都会给神经网络加一层权重，训练结束后可以用这些权重初始化一个深度的监督学习神经网络或者直接把得到的深度特征作为其他监督学习预测器的输入，或者会对预训练阶段得到的整个网络进行监督精调。

贪心逐层无监督预训练(greedy layer-wise unsupervised pretraining)，是指一个任务(无监督学习，尝试获取输入分布的形状)的表示对另一个任务(具有相同输入域的非监督学习)有帮助。贪心逐层无监督预训练依赖于单层表示学习算法，比如RBM（受限玻尔兹曼机器），单层自编码器，稀疏编码等其他学习潜在表示的模型。每一层使用无监督学习预训练，将前一层的输出作为输入，输出数据的新的表示。这个新的表示的分布可能更简单。

基于无监督标准的贪心逐层训练过程最早被用来规避监督学习问题中深度神经网络难以联合训练多层的问题。这种贪心学习过程可以为多层联合训练过程找到一个好的初始值。目前训练全连接的深度结构时，无需再使用贪心逐层无监督预训练，但是无监督预训练是第一个成功的方法。

贪心逐层无监督预训练，之所以贪心是因为他是一个贪心算法，每一步独立的优化解决方案的一部分，而不是联合优化所有部分。之所以逐层是因为每一次处理一层网络，训练第k层时保持前面的网络层不变。之所以无监督时因为每一层都是用无监督表示学习算法训练的。之所以叫预训练时因为整个预训练过程时在联合训练算法精调所有层之前进行的。

无监督预训练结合了两种不同的想法。其一，它利用了深度神经网络对初始参数的选择可以对模型有着显著的正则化效果的想法。其二，它利用了学习输入分布有助于学习输入到输出的映射的思想。

5、单层学习模块

并非某个或某种模型，是一个只有一个隐藏层或者隐变量层的组件
表示学习的发展主要发展为两派：概率图模型和神经网络。一个深度模型被描述为概率图还是神经网络的主要差别在于它的层级结构被解释为描述概率图的还是描述计算图的。简单解释就是隐藏单元被解释为随机变量还是计算节点。

两个领域都关注于单层的贪心学习模块和单层模型类型间的相似性。比如，受限玻尔兹曼机RBM属于概率派，自动编码器属于神经网络这边。RBM通过引导式的原则(score matching)来训练模型而自动编码器是正则化的重构目标来训练的。另外一个联系是，计算模型计算表示的计算图可以对应到概率模型的推断过程。随着深度的加深，二者的差异越来越小了。
一个无监督的单层表示学习算法，它扩展了所有三个视图：概率学习、自动编码器学习和流形学习
（例子）PCA三种解释：
（1）与概率模型相关，例如probabilistic PCA、factor analysis和传统的多元变量高斯分布
（2）PCA学到的表示和基础的线性自编码器基本一致
(3) PCA也可以视作线性流学习的简单线性转化，即在输入空间密度集中区域附近刻画了一个低维的区域。

6、概率模型

6.1、有向图模型

有向的因变量模型分别参数化条件似然p(x | h)和先验分布p(h)来构建来联合分布即p(x,h) = p(h)p(x | h)。

有向模型的一个重要属性就是迁移解释(explaining away)。即一个与事件独立的原因(先验)在给定观测数据下可以变得非独立。隐式因子模型也可以叫做隐式因果模型，其中h解释为观测数据x发生的原因。

例子，“假如你在度假，此时家里的警铃报警了，你会第一时间想到家里遭贼了。但是你随后听广播说你家附近地震了。如果你事先知道地震的话，你就可以很大程度上觉得警报响不是因为家里进贼了“。这个小故事中，把两个完全不相干的事即入室盗窃和地震通过警报这一事件联系在一起。这种相关性是手动引入的，这样就实现了用一个事件的观察信息解释另外一个事件。

最后，要计算特征表示即找到h的后验分布，计算量会非常大。而迁移解释保证可以找到一个略次的后验也可以提供一些有用的信息。

稀疏编码(sparse coding)是迁移解释一个非常好的例子，即使在一个过完备的字典中，稀疏编码使用MAP（Maximum a Posteriori 最大后验）推断过程寻找h时，可以找到最适合的基并给其他的赋0尽管它们和输入有较高的相关性。

6.2、无向图模型

无向图模型也叫马尔可夫随机场，通过一组非归一化的非负最大团势函数的乘积参数化联合概率P(x, h)。玻尔兹曼机的能量函数通过玻尔兹曼分布确定了在关于x，h的概率分布。即

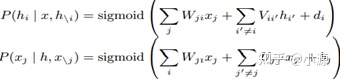
但是，一般情况下，玻尔兹曼机的推断过程时难以计算的。而受限玻尔兹曼机通过约束节点间的交互使推断成为可能。即，RBM的特征表示可以表示为一组后验边缘分布P(hi | x)。

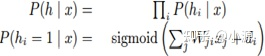
6.3、RBM（受限玻尔兹曼机器）对实值数据的推广

几种改进
RBM中推理和学习的可追溯性启发了许多作者，通过对其能量函数的修改来扩展它，以建模其他类型的数据分布
（1）GRMB：增加x^2的偏差值（唯一变化），GRBM未能充分捕获自然图像的统计结构，其根源在于模型容量的唯一使用，即以条件协方差为代价获取条件平均值。但是，自然图像的主要特征是像素值的协方差，而不是它们的绝对值。
（2）均值和协方差mean and covariance RBM (mcRBM) ——双层BM： 与GRBM不同的是，mcRBM使用它的隐藏层来通过两套隐藏单元来独立地参数化数据的均值和协方差。
（3）mPoT model (mean-product of Student s T-distributions model： 一种基于能量的模型，其中对隐藏变量的可见单元的条件分布是一种多元高斯(非对角协方差)，而在已知的隐变量上的附加条件分布是一组独立的伽玛分布。 应用：合成大规模的自然图像
（4）spike-and-slab Restricted Boltzmann Machine (ssRBM)目的：使隐藏单元对均值和协方差信息进行编码。
（5）总结 ：
mcRBM、mPoT和ssRBM均对实值数据进行建模，使隐藏单元不仅对数据的条件均值进行编码，而且对其条件协方差进行编码。
mcRBM和mPoT使用隐藏单元的激活来加强对x的协方差的约束，ssRBM使用隐藏单元沿对应的权重向量指定的方向缩放精度矩阵。当隐含层的维度与输入的维度有显著差异时，这两种建模条件协方差的方法是不同的。
mPoT和mcRBM似乎并不适合在过于完整的设置中提供稀疏表示。

6.4、RBM参数估计

对于每个梯度更新步骤，我们将开始一个吉布斯采样链，等待该链收敛到平衡分布，然后抽取足够数量的样本来近似于等式中相对于模型（联合）分布的期望梯度然后重新启动该过程，以便在对数似然值上进行近似梯度上升的下一步步骤。这一过程有一个明显的缺陷，即等待吉布斯链“老化”，并对每次梯度更新重新达到平衡，不能成为实际训练算法的基础。
针对Gibbs链老化的方法
（1）对比散度： 缩短Gibbs采样链，以减少基于从短期运行的吉布斯采样器样本的负面期望的方差。虽然从非常短的吉布斯链中抽取的样本可能是模型分布的严重偏倚(和差)表示，但它们至少在模型分布的方向上移动。
（2）随机极大似然：使用一个持续运行的吉布斯链(或者通常是并行运行的吉布斯链数)，从中抽取样本来估计负相期望。 尽管更新之间的模型参数发生了变化，但这些变化足够小。
（3）伪似然性和比率匹配：伪似然寻求将形式P (Xd | Xnd)的所有一维条件分布的乘积最大化，而比值匹配可以解释为分数匹配的扩展到离散数据类型。
（4）其他训练原则：噪声对比估计(Gutmann and Hyvarinen, 2010)，其中训练准则转化为概率分类问题:区分(正)训练样本和(负)由广义分布产生的(如高斯分布)的噪声样本；基于CD的 依赖于区分正面的例子(训练的分布)和一些消极的例子

7、学习一个从输入直接到表示的参数化表示

在概率模型中，学习到的表示是直接与隐变量相关的，具体是在给定观测变量后与隐变量的后验分布相关。但是这些后验分布一般很难计算随着大量层之间的交互。并且这些后验并不是一个简单的可以直接拿来用的特征向量，所以还需要后续的采样或者其他操作比如计算隐变量的期望或者边缘密度来找到最有可能的特征值。所以我们很需要一种可以直接在最后提取确定性的特征值的方法。

7.1、自编码器

训练自动编码器变体的一个实际优点是：它们定义了一个简单的可跟踪优化目标，可以用来监视进程。 为了将重构误差最小化，以捕获数据生成分布的结构，因此，在训练准则或参数化过程中，一定要防止自动编码器学习自身函数，从而在任何地方产生零重建错误。基础的auto-encoder训练在于找到一个值的参数向量θ，以重建误差最小化。

7.2、正则自动编码器

与PCA一样，自动编码器最初被视为一种降维技术，因此使用了一个瓶颈，即dh < dx。另一方面，稀疏编码和RBM方法的成功使用往往倾向于过完全表示，即dh > dx。这可以允许自动编码器简单地复制特征中的输入，并进行完美的重建，而无需提取更有意义的特征。最近的研究已经证明了非常成功的替代方法，称为正则自动编码器，来“约束”表示，即使它是过度完整的。
两个正则化的自动编码器的变体:收缩的自动编码器通过使编码器收缩来减少表示(在每个点附近)的有效自由度的数量（使编码器的导数小(从而使隐藏单元饱和)），而去噪自动编码器使整个映射更加健壮（鲁棒性更好）（对微小的随机扰动或收缩不敏感，确保在训练样本周围的大部分方向上，不能很好重建。

7.2.1：稀疏自编码器

表示中的稀疏性可以通过惩罚隐藏单位偏差，当直接惩罚隐层单元时，有很多变体，但没有文章比较他们哪一个更好。

7.2.2：去噪自编码器

去除一个人工制造的噪声点，指向附近高密度的
Vincent2010中考虑了对灰度图加入等向高斯噪声、椒盐噪声

7.2.3：收缩性自编码器（CAE）

将学习特征的灵敏度与输入的无穷小变化相结合
拥有更好性能原因：
（1）特征的敏感性是直接的，而不是重建的敏感性;
（2）惩罚是分析性的，而不是随机的:一个有效的可计算表达式取代了原本可能需要的dx腐败样本的大小(即dx方向的灵敏度);
（3）hyper-parameter超参数λ允许精细控制的重建与鲁棒性之间的权衡。
CAE分析惩罚的一个潜在缺点是，它只会鼓励对输入的无穷小变化的鲁棒性。
CAE的学习表示往往是饱和的，而不是稀疏的

7.2.4：预测稀疏分解

PSD可以看做是sparse coding的近似，只是多了一个约束，可以将稀疏编码近似为一个参数化的编码器。

8、流形学习角度看表示学习

表示学习的另一个重要角度就是基于流形的几何概念。流形学习假设现实中我们观察到的高维数据是低维数据在高维的映射。对于表示在流形学习中的理解，我们可以思考一个流形，他是输入空间的一个变化，可以在学到的表示中被反应出来或被获取到(通过对输入空间的变化得到一个流形)。流形学习注重的是数据的拓扑结构，变化方向等。所以流形的一些正切方向会被很好的观察到而正交与流形的则会被忽略。所以首要的无监督学习任务可以视作对数据支持(data-supporting)的流形的结构建模。相应的表示可以用嵌入的流形上的坐标系来表示。这个话理解起来比较绕口，其实类似于PCA降维，找到主要的成分，用这些留下来的成分联合表示要学习的特征。流形学习的主要思想还是借鉴拓扑学中流形的概念即一组周围连续的点，把高维的数据理解为低维的流形结构，相当于做了降维的操作

8.1、学习基于邻域图的参数映射

（1） 基于训练集的邻域图： 通常是从训练点之间的成对欧几里得距离推导出来的
原理：这些坐标现在通过在输入空间坐标上的显式参数化函数得到，它的参数是要学习的。
在非参数化版本中，同样的优化目标可以通过梯度下降最小化:现在，在嵌入的坐标上，梯度下降不再是梯度下降，而是反向传播到映射函数的参数
（2） 学习直接编码的方法是半监督嵌入：
一个深度参数化的神经网络体系结构同时学习了多重嵌入和分类器。
在优化监督分类成本的同时，训练标准还利用每个训练实例的训练集邻域来鼓励在改变一个邻居的训练样本时，中间层次的表示保持不变。然而，在高维度空间(由于维数的限制而导致稀少)的基础上，基于训练集邻里关系的模型建立模型，可能是有风险的，因为大多数的欧几里得近邻的邻居在语义上都有太少的风险。

8.2、学习表示非线性流形

在非线性表征学习算法中，可以很方便地考虑输入中的局部变量。即使配对是随机挑选的，在获得一个对优化目标有重大影响的指标之前，也必须考虑很多。 对于与非饱和隐藏单元相关联的输入空间方向，x的计算表示法只会非常敏感(如sigmoid层的雅可比矩阵）。精确的低维流形模型(如PCA)会产生非零的奇异值，这些值与流形上的方向相关联，而与流形正交的方向则是精确的零。但是在平滑的模型中，例如收缩自动编码器或RBM，我们将会有较大的相对较小的奇异值(相对于非零和完全为零的)。CAE确实模拟了一个低维流形的切线空间。主要的奇异向量构成了估计流形的切平面的基础。

8.3、利用建模的切线空间。

在流形上的一个点上，局部的切线空间可以考虑捕捉在训练数据中突出的局部有效转换。在数据流形上的这种非常局部的转换不希望改变类的标识。为了构建它们的歧义分类器(MTC)，采用切距等技术，构建对输入变形不敏感的分类器。 应用于由CAE中的局部主切线方向，即不使用任何先验知识(除了广泛的先验存在之外)。

9、概率编码模型和直接编码模型之间的联系

概率模型的标准似然框架分解了参数θ模型的训练准则分为两部分：对数似然对数P（x|θ）（或日志P（x|hθ）潜在变量h），和先前的日志P(θ)（或日志P（h|θ）+日志P(θ)潜在变量）。

9.1、PSD：一种概率性解释

在PSD算法中，可以在上述标准概率视图和直接编码计算图之间建立连接
PSD是一个介于概率模型和直接编码方法的表示学习算法。PSD位于概率模型（带有潜在变量）和直接编码方法（直接参数化映射）的交叉点。

9.2、正则化自编码器捕获密度的局部结构

正则化的自动编码器的概率解释：规则化的AE训练准则不同于标准的似然估计因为他们需要一种前置，因此他们是依靠数据的。规则项需要学习到的表示尽可能的对输入不敏感，然而在训练集上最小化重构误差又迫使表示包含足够的信息来区分他们。

9.3、学习近似推理

当需要迭代推理时，在具有潜在变量的概率模型中是如何计算表示的。有一个计算图（在MCMC的情况下，可能在某些节点中使用随机数生成）将输入映射到表示，对于确定性推理（例如，MAP变分推理或变分推理），该函数可以直接优化。这是一种概括PSD的方法，在最近的推理和学习交叉的概率模型工作中已经探索。其中一个中心思想是，与其使用通用的推理机制，可以使用一个学习和更有效的推理机制，利用它所应用的数据类型的细节。

9.4、采样挑战

一个令人不安的挑战与许多概率模型与潜在变量像大多数玻尔兹曼机器变量是好MCMC采样需要作为学习过程的一部分，但采样变得非常低效（或不可靠）训练进展
MCMC（马尔科夫蒙特卡罗）采样效率很低，学习分布的模型变得更加清晰，使得模型之间的混合非常缓慢。 Bengio2012表明深层表示可以帮助混合。

9.5、评估和监控性能

一般情况下我们在学习到的特征上加一层简单的分类器，但是最后的分类器可能计算量更大（例如fine-tuning一般比学习特征需要更多次数的迭代）。更重要的是这样可能给出特征的不完全的评价。
对于AE（自编码器）和sparse coding（稀疏编码）来说，可以用测试集上的重构误差来监视。对于RBM（受限玻尔兹曼机）和一些BM（玻尔兹曼机），Murray2008提出用Annealed Importance Sampling来估计partition function（分配函数）。RBM的另一种（Desjardins2011）是在训练中跟踪partition function，这个可以用来early stopping和减少普通AIS的计算量。

10、深度模型全局训练(区别是全局训练，所有层次联合培训)

深度架构提出的最有趣的挑战之一是：我们应该如何共同训练所有级别？在前一节和第4节中，我们只讨论了如何将单层模型组合成一个深度模型。在这里，我们考虑了所有层次的联合培训和可能出现的困难。

10.1、培训深度架构的挑战

更高层次的抽象意味着更多的非线性。 高级抽象需要更少的数据进行学习，但是由于增加了非线性，使得更抽象的表示函数和训练都更困难。无监督或监督分层的培训更容易，这可以利用将单层模型叠加到较深的模型中。先学习更简单的概念，然后在简单的概念之上构建更高层次的概念。
第一种实现就是非监督或者监督单层训练，Erhan2010解释了为什么单层非监督预训练有帮助。这些也与对中间层表示有指导作用的算法有联系，例如Semi-supervised Embedding（Weston2008）。
在Erhan2010中，非监督预训练的作用主要体现在regularization effect（正则化效应）和optimization effect（优化效应）上。前者可以用stacked RBM或者AE实验证明。后者就很难分析因为不管底层的特征有没有用，最上面两层也可以过拟合训练集。
改变优化的数值条件对训练深层结构影响很大，例如改变初始化范围和改变非线性函数（Glorot2010）。第一个是梯度弥散问题，这个难题促使了二阶方法的研究，特别是Hessian-free second-order方法（Marten2010）。Cho2011提出了一种RBM自适应的学习速率。Glorot2011表明了sparse rectifying units也可以影响训练和生成的表现。
Ciresan2010表明有大量标注数据，再合理的初始化和选择非线性函数，有监督的训练深层网络也可以很成功。这就加强这种假设，当有足够的标注样本时，无监督训练只是作为一种prior。Krizhevsky2012中运用了很多技术，未来的工作希望是确定哪些元素最重要，怎么推广到别的任务中。

10.2、深度玻尔兹曼机的联合训练

联合训练的所有层的一个特定的无监督模型——深度玻尔兹曼机(DBM)， DBM拥有多层隐藏单元，在奇数层中有条件独立于偶数层的单元，反之亦然。
Salakhutdinov and Hinton (2009)提出了DBM。
DBM的能量方程：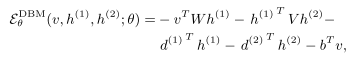

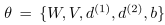
DBM相当于在Boltzmann Machine的能量方程中U=0，并且V和W之间稀疏连接结构。

10.2.1均场近似推理

因为隐层单元之间有联系，所以后验概率变得棘手，上文中用了（mean-field approximation）平均场近似。比如一个有两层隐层的DBM，我们希望用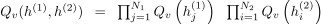
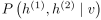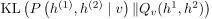近似后验，使得最小。

10.2.2训练深度玻尔兹曼机

训练DBM时，与训练RBM最主要的不同在于，不直接最大似然，而是选择参数来最大化下界（lower-bound）

11、构建不变式

我们知道整合一些领域内的先验知识对机器学习很有帮助。但是目前的算法主要只考虑的是对高维数据的一般化的归纳偏执，这使得这些算法可以处理任何高纬度的问题。因此，我们一般会更倾向于输入数据最基础的领域知识。
构建不变特征的目的是消除表示对当前任务不具信息性的数据中的方差方向的敏感性。构建不变特征的过程可以看作由两个步骤组成。首先，恢复用于数据的低级特征。其次，将这些低层特征的子集集合在一起，形成高层不变特征。

11.1生成转换后的示例

Ciresan2010中使用了一些小的放射变换来扩大训练集MNIST，并取得了很好的结果。

11.2卷积和池化

(Le Roux et al., 2008a)研究了图片中的2D拓扑。
论述这种结构与哺乳类动物的大脑在目标识别上的相同点：
Serre et al., 2007：具有类皮层机制的鲁棒对象识别
DiCarlo et al., 2012：大脑如何解决视觉对象识别？
Pooling的重要性：
Boureau2010：视觉算法中特征池的理论分析
Boureau2011：:问本地:图像识别的多路本地池
一个成功的pooling的变种是L2 Pooling：
Le2010：平铺卷积神经网络
Kavukcuoglu2009：通过地形过滤器地图学习不变特征
Kavukcuoglu2010：学习卷积特征层次的视觉识别
Patch-based Training:
(Coates and Ng, 2011)：编码与稀疏编码和矢量量化训练的重要性
这篇文章比较了基于补丁的训练的几个特征学习器，并在几个分类基准上达到了最先进的结果。
文中发现最后的结果与简单的k - means聚类方法类似,可能是因为本补丁来就是低维的,例如边缘一般来说就是6 * 6,不需要分布式的表示
Convolutional and tiled-convolutional training（卷积和平铺卷积训练:）:
convolutional RBMs：
Desjardins and Bengio, 2008：视觉卷积RBMs的经验评估
Lee，2009：用于分层表示的可扩展无监督学习的卷积深度信念网络
Taylor，2010：时空特征的卷积学习
a convolutional version of sparse coding:
Zeiler2010:反卷积网络
tiled convolutional networks:
Gregor&LeCun,2010:具有局部接受野的时间产品网络中出现复杂样细胞
Le,2010:平铺卷积神经网络
Alternatives to pooling: (Scattering operations)（池化的替代方案:(分散操作)）
Mallat,2011: Group invariant scattering（群不变散射）
Bruna&Mallat,2011: Classification with scattering operators（散射算子分类）

11.3时间相干性和慢性特征

最简单的是时间t和t + 1时特征值的平方差。其他可能的时间一致性先验包括以下内容。首先，惩罚绝对值（或类似的稀疏性惩罚），而不是惩罚平方变化，这将说明大多数时候变化应该恰好是0，这对我们周围的现实因素是有意义的。其次，人们会认为，不同的因素可能与它们自己不同的时间尺度相关联，而不只是缓慢变化。因此，它们的时间尺度的特异性可以成为解开解释因素的一个线索。第三，人们会期望一些因素真的应该由一组数字（如x、y、z的位置和Hinton等人（2011）的姿态参数）来表示，而不是由一个标量来表示，并且这些组倾向于一起移动。结构化稀疏性处罚（卡武库格鲁等，2009年；杰纳顿等，2009年；巴赫等，2011年；格雷戈等，2011年）可用于此目的。

11.4分解变异因子的算法

Hinton，2011：Transforming auto-encoders这篇文章利用数据中已知存在的一些变化因素。
Erhan，2010：Understanding representations learned in deep architectures这篇文章有实验表明DBN的第二层倾向于比第一层更具有不变性。

12、结论

本文讲述了三种表示学习方法：概率模型、与自动编码器相关的重建算法和几何流形学习方法。
实际注意事项及指引:它们有许多超参数和变体，探索它们的配置和架构是一门艺术
结合通用AI级先验:我们期望未来表示学习的成功应用能够改进和增加先验列表，并将其中的大部分合并起来，而不是只关注一个。训练标准的研究更好地考虑这些先验，可能会使我们更接近发现学习算法的长期目标，可以解开潜在的解释因素
推理：基于直接参数化表示函数的方法将包含越来越多的人们在概率潜在变量模型的推理过程中发现的迭代计算类型
优化：在有监督的情况下（最近有许多成功）和无监督的情况下（需要做更多的工作）的情况下，以及训练深度架构的失败。虽然正则化效应在小的数据集上可能很重要，但在非常大的数据集上持续存在的影响表明，这涉及到一些优化问题。它们更多的是由于局部最小值（我们现在知道有大量的它们）和训练程序的动态吗？或者它们主要是由于不良条件，可以通过近似二阶方法处理？这些基本问题仍然没有得到解答，值得进一步研究

13、表示学习思维导图

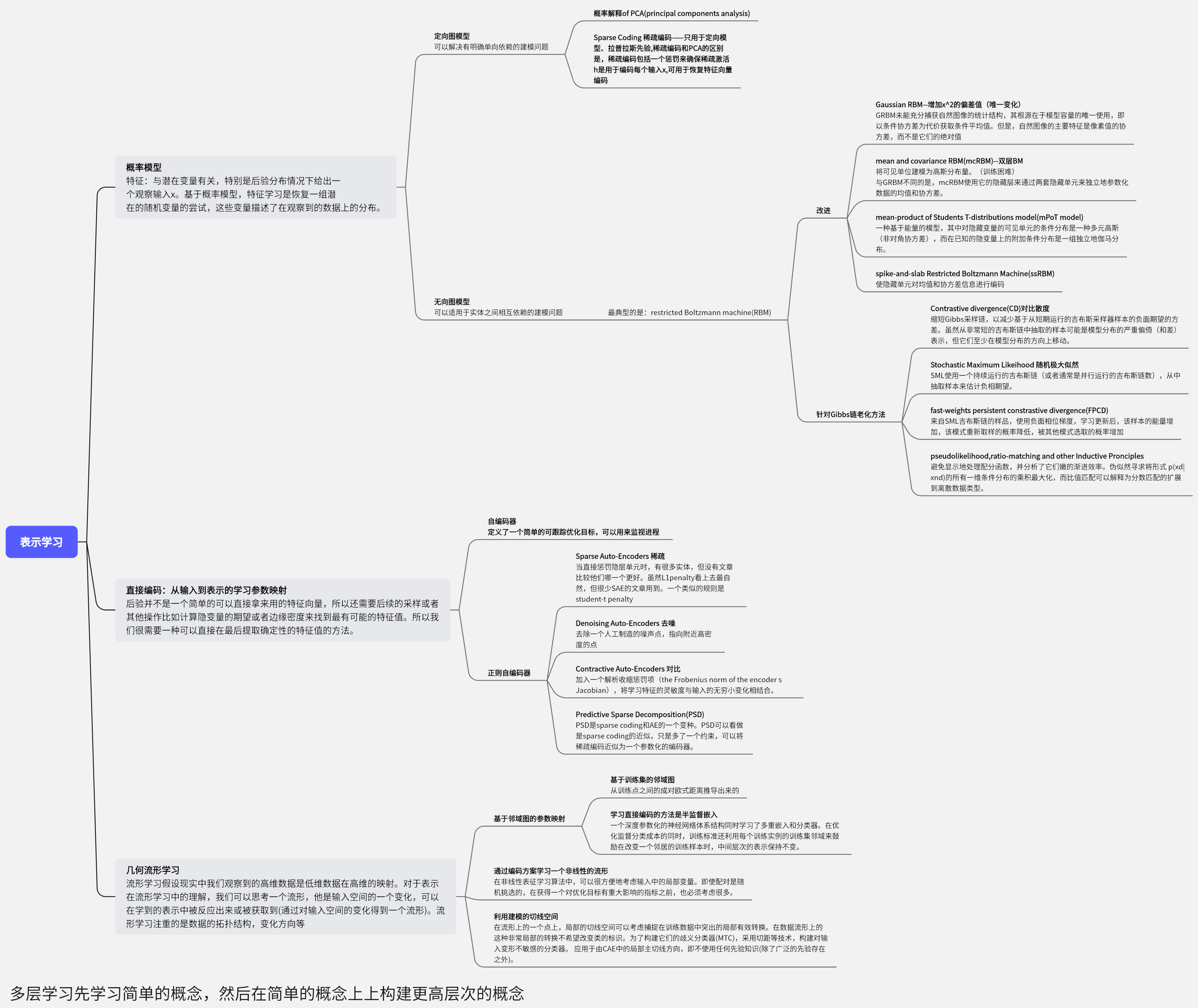
14、问题

问题1：第十节和第四、九节区别是什么？

第四、九节是将单层模型组合成一个深度模型。
例子：贪心逐层无监督预训练，之所以贪心是因为他是一个贪心算法，每一步独立的优化解决方案的一部分，而不是联合优化所有部分。之所以逐层是因为每一次处理一层网络，训练第k层时保持前面的网络层不变。之所以无监督时因为每一层都是用无监督表示学习算法训练的。之所以叫预训练时因为整个预训练过程时在联合训练算法精调所有层之前进行的。
第十节是共同训练所有级别，所有层次进行联合培训。
前者叠加单层，后者联合所有层。

问题2：概率模型为什么要提出来？

从概率建模的角度来看，特征学习的问题可以被解释为一种试图恢复一组简约的潜在随机变量，这些变量描述了观察数据上的分布。我们可以用潜在变量h和观测数据或可见变量x的联合空间来表示p（x，h）的概率模型。特征值被认为是一个推理过程的结果，以确定给定数据的潜在变量的概率分布，即p（h | x），通常被称为后验概率。学习的构想是估计一组模型参数，（局部）最大限度地提高训练数据的正则化可能性。概率图形模型形式主义给了我们两种可能的建模范式，我们可以考虑推断潜在变量的问题，定向和无向图形模型，不同的参数化的联合分布p（x，h），产生重大影响的性质和计算成本的推理和学习。
概率图模型（或简称图模型）在形式上是由图结构组成的。图的每个节点（node）都关联了一个随机变量，而图的边（edge）则被用于编码这些随机变量之间的关系。概率图模型可以简单的理解为“概率+结构”，即利用图模型来结构化各变量的概率并有效、清晰的描述变量间的相互依赖关系，同时还能进行高效的推理，因此在机器学习中概率图模型是一种应用广泛的方法。
概率图模型中的术语图指的是图论，也就是带有边和点的数学对象。确切地说，概率图模型（Probabilistic Graphical Models，PGM）是指：你想描述不同变量之间的关系，但是，你又对这些变量不太确定，只有一定程度的相信或者一些不确定的知识。
对于这个世界的任何物质，大到整个宇宙小到分子原子，其出现和演化的规律均存在一定的不确定性，而从另一个角度进行观察我们则可通过概率来描述。同样对于对于深度学习，我们可以理解为在给定样本下，我们通过神经网络学习出其内在的深层抽象特诊表示，进而对未知的样本进行估计和推断。其中样本的分布规律我们可以通过概率分布进行刻画，而推断的结果的不确定性我们也可以利用概率来表示。因此概率模型（probabilistic model） 为机器学习打开了一扇新的大门，其将学习任务转变为计算变量的概率分布。然而在实际情况中却是各个变量间存在显示或隐示的相互依赖，若我们直接基于训练数据去求解变量的联合概率分布这无论在时间复杂度还是空间复杂度上均是不可信的或不划算的。那么，我们如何有效（高效）紧凑且简洁的表示和计算它们的联合分布概率或条件概率呢，这里便引入了图的概念。通过充分利用变量间的依赖关系、或条件独立假设，我们可以大大简化参数求解的计算开销