【BUAA 软工个人项目作业】玩转平面几何
BUAA 软件工程个人项目作业
| 项目 | 内容 |
|---|---|
| 课程:2020春季软件工程课程博客作业(罗杰,任健) | 博客园班级链接 |
| 作业:BUAA软件工程个人项目作业 | 作业要求 |
| 课程目标 | 学习大规模软件开发的技巧与方法,锻炼开发能力 |
| 作业目标 | 完成第一次个人项目 |
| 教学班 | 周五上午006班 |
| 项目GitHub地址 | GitHub链接 |
PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 60 | 80 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 40 | 32 |
| · Design Spec | · 生成设计文档 | 30 | 45 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 20 | 16 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 5 | 3 |
| · Design | · 具体设计 | 60 | 48 |
| · Coding | · 具体编码 | 360 | 373 |
| · Code Review | · 代码复审 | 60 | 49 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 83 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 50 | 68 |
| · Size Measurement | · 计算工作量 | 5 | 5 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 10 | 24 |
| 合计 | 760 | 826 |
解题思路
基础题
在一开始拿到题目时,简单看了一下两道题,发现两道题中第二题是相较第一题进行拓展的,并且题目所要解决的问题是求解现实生活中看得见摸得着的集合问题,因此一开始就决定用面向对象的思路来设计代码。题目描述中有点,线,坐标值的概念,因此决定构造以下几个类:
RationalNumber:有理数类RationalPoint:由有理数作为坐标值的点Line:直线类GeometryStatistic:统计类,记录直线,点个数。Reader:输入处理类。
在看到题目后,看第一题的题意,一个顶点至少经过两条直线的本意其实就是直线的交点。想到求直线的交点,我们已知对于两条直线求交点,不过是求解一个二元一次方程组,并且其解是可以由直线的参数表示的。因此当我们求两条直线的交点时,这个步骤是可以做到\(O(1)\)的。即假设两条直线分别为:
若直线之间存在交点,则假设交点为\((x_0, y_0)\),联立方程可以解得
那么当给定每一条直线的两个顶点时,代数式可以化简为
当然,要考虑其中的特殊情况,若\(k_1\)无穷大时,则将\(k_2\)替换\(k_1\)(当两条直线必然相交时\(k_1\)和\(k_2\)不可能同时为无穷大)。
考虑到点坐标的精度问题,由于两条直线可能斜率相差很小,交点又非常的远,因此为了防止出现double的精度缺失情况,决定构建一个类RationalNumber,这个类来描述一个有理数,用分数的形式表示。这样在第一题里,所有的点坐标即可以用有理数来表示,这样必然能保证准确地比较出两个不同的交点。
但问题中要求解的是所有直线的交点,其中直线的最大数目可以达到\(1000000\)条,这说明如果用最简单的两两直线相交的方式暴力求解,时间复杂度为\(O(n^2)\),其结果必然超时。但由于没有想到更好的优化算法,因此决定从数据结构角度来解决这一个问题。
通过查阅资料找到,cpp中有一种和Java的HashSet类似的数据结构,为\(unordered_set\),当其中存在自定义的类时,需要重写hash和equal接口,其中本人设计的hash和equal接口如下:
size_t my_hash::operator()(RationalPoint* const& a) const {
return hash<string>{}(a->hashstring);
}
bool my_equal::operator()(RationalPoint* const& a, RationalPoint* const& b) const {
return a->equals(*b);
}
其中RationalPoint即为构建的点类,其两个分量为xy两个有理数坐标值,自定义的hash函数为将点坐标变成我们认知的字符串形式,在求字符串的hash值,equal的比较更为显然,即比较两个分量是否分别相等。
附加题
由于附加题中引入了圆的概念,因此需要增加以下几个类:
Circle:圆类UnRationalPoint:无理数点类,即两个顶点分量有一个为无理数
和直线求交点同理,引入了圆之后,交点又以下几种情况:
- 线线交点
- 线圆交点
- 圆圆交点
其中线线交点第一题已经求得,线圆交点同理,可以联立二次方程求解
可以解得:
其中,更号内的表达式可能小于0,若小于0则说明没有交点,返回即可;k可能无穷大,若k无穷大,则x为直线的任意一个顶点的x坐标值,y带入圆方程即可计算得到。
圆圆交点可由以下定理计算:两个圆方程作差表达式,为圆的交线,先求的圆的交线,再带入到线圆交点计算,得到交点。注意圆的相离情况特判。
计算得到的交点,有的坐标值可能均为有理数,有的可能为无理数,有理数和无理数的判断即根据求解方程中的更号开更后是否为整数来判断。若开更后为整数,则为有理数,放入有理数类中,若为无理数,则以double表示点坐标,放入无理数类中。
考虑到精度问题,由于圆的半径和顶点有限,因此所交的点不会到很远的地方,因此和直线相交的点精度不会太细。这次题目比较double的精度以1e-10来考虑。
设计过程
基础题
RationalNumber类
该类来表示有理数,其中有两个属性值分别为分子和分母,类型均为long long,有以下几个成员函数:
- 构造函数:传入分子分母,辗转相除法求最大公约数后进行化简,符号放在分子处。
equals(RationalNumber a):比较两个有理数是否相等toString():将有理数转为字符串
RationalPoint类
该类用来表示点坐标值为有理数的顶点,即两直线交点,有x,y两个分量,类型为有理数类,有成员函数:
- 构造函数:传入两个分量
equals(RationalNumber a):比较两个有理数顶点是否相等toString():将有理数顶点转为字符串
Line类
直线类,该类来存储题目所给的直线,由于给的坐标值为整数,因此该类有四个分量,分别为x1, x2, y1, y2,类型为int,有成员函数:
- 构造函数:传入两个顶点坐标
GeometryStatistic类
该类为统计类,统计图中的直线,以及求直线交点,有成员变量vector<Line> lines记录直线,以及unordered_set<RationalPoint*, my_hash, my_equal>保存已经求得的交点,其中my_hash和my_equal为自定义的接口,负责为RationalPoint*生成hash值和比较,具体定义见上边代码。有成员函数:
feed(Line line):添加直线,并求新的交点line_line_intersect(Line l1, Line l2):计算两个直线的交点。getPointCount():获取当前所有交点个数
Reader类
该类为输入输出处理类
程序流程
- main函数读取命令行参数,构造Reader实例,初始化输入输出文件,构造GeometryStatistic对象。
- Reader读取输入,每读取完一条直线,调用GeometryStatistic的feed函数,将直线注入统计
- 直线在feed函数中,首先和之前已经加入的所有直线进行一次遍历,调用
line_line_intersect函数求解交点 line_line_intersect函数使用上述推导的公式,构造交点坐标的有理数对象,并将有理数对象insert到unordered_set中。- 当读完输入文件后,读取
Statistic对象中getPointCount()的值,输出到文件,程序结束。
单元测试构造
- 在写完有理数类后,构造单元测试,测试构造的有理数是否有按要求化简。
- 在写完有理数和有理数顶点后,其中重载了
my_hash和my_equal接口后,构造相应的单元测试,实例化一个unordered_set对象,检验两个接口是否满足要求 - 在写完交点求解后,构造单元测试,测试
Statistic类,是否能够正确计算交点并存储。
附加题
增加类:
Circle类
圆类,存储圆的顶点和半径
UnRationalPoint类
无理数顶点类,存储的顶点只要其中一个分量为无理数,就进行存储。
完成该类时,同样需要重载hash和equal接口。其中需要注意精度问题,考虑到1e-10;
GeometryStatistic类增加函数
line_circle_intersect(Line l, Circle c):求解直线和圆的交点,根据上述推导公式求解。其中开更号时判断是否为有理数,若为有理数则构建RationalPoint对象实例并存到相应的set中,若为无理数则构造UnRationalPoint实例并存到相应的set中circle_circle_intersect(circle c1, circle c2):同理,需要区分有理数和无理数
程序流程
- main函数读取命令行参数,构造Reader实例,初始化输入输出文件,构造GeometryStatistic对象。
- Reader读取输入:
- 每读取完一条直线,调用GeometryStatistic的feed函数,将直线注入统计
- 每读取完一个圆,调用GeometryStatistic的feed函数,将圆注入统计
- 在feed函数中:
- 直线在feed函数中,首先和之前已经加入的所有直线进行一次遍历,调用
line_line_intersect函数求解交点,再遍历所有的圆,调用line_circle_intersect求解和圆的交点,并将交点加到相应的set中 - 圆在feed函数中,首先和之前已经加入的所有直线进行一次遍历,调用
line_circle_intersect函数求解交点,再遍历所有的圆,调用circle_circle_intersect求解和圆的交点,并将交点加到相应的set中
- 直线在feed函数中,首先和之前已经加入的所有直线进行一次遍历,调用
- 当读完输入文件后,读取
Statistic对象中getPointCount()的值,输出到文件,程序结束。
代码优化
使用一组较大的数据,来观测性能是否达标,分析结果如下:
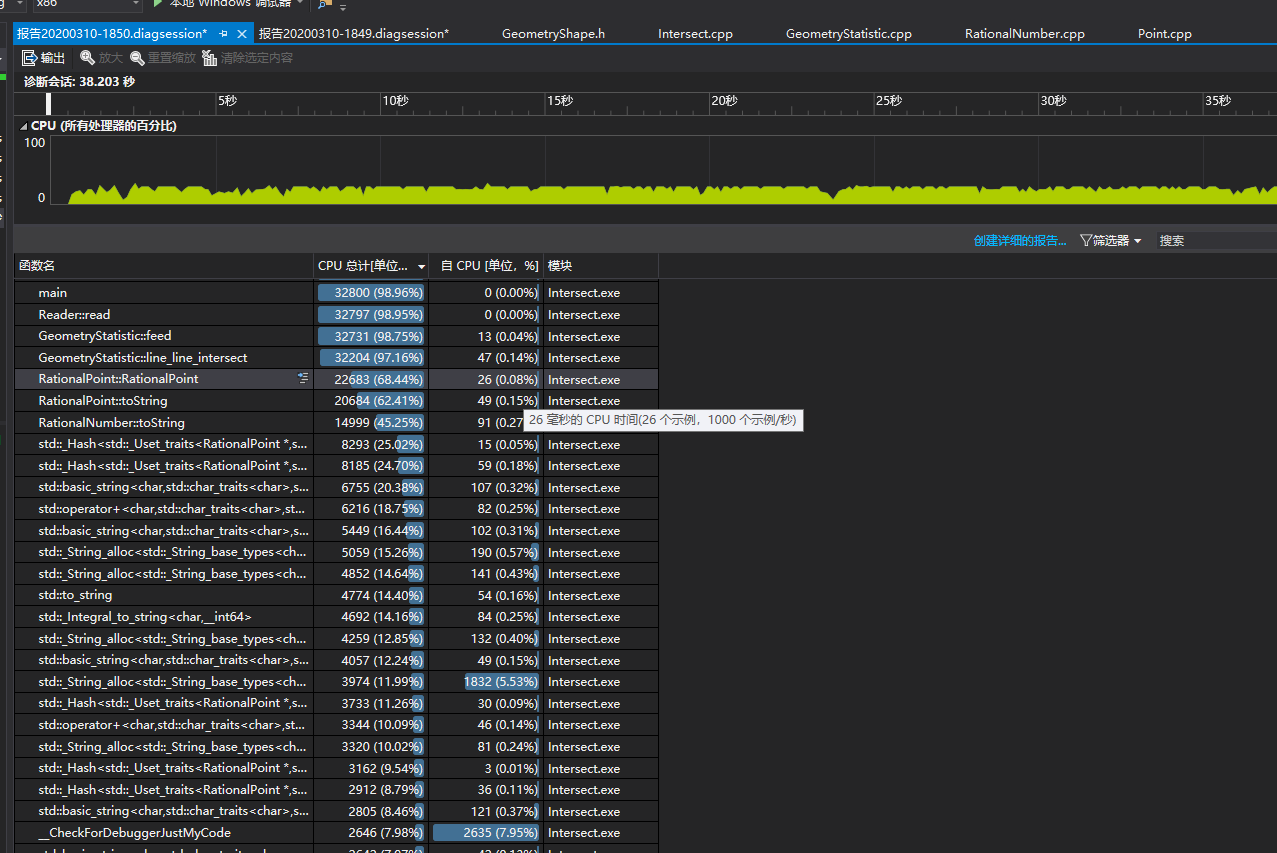
其中可以发现,除了main函数和各类构造函数之后,运行的瓶颈在于toString函数,这个函数是用来构造hash值的,但是由于toString函数太过于影响效率,因此考虑更换哈希函数的计算,不要用toString。
代码说明
RationalPoint::RationalPoint(RationalNumber &x, RationalNumber &y) {
this->x = x;
this->y = y;
this->hashstring = this->toString();
//cout << toString() << endl;
}
RationalPoint::RationalPoint() {}
bool RationalPoint::equals(const RationalPoint &a) const {
return x.equals(a.x) && y.equals(a.y);
}
string RationalPoint::toString() const {
return x.toString() + "," + y.toString();
}
size_t my_hash::operator()(RationalPoint* const& a) const {
return hash<string>{}(a->hashstring);
}
bool my_equal::operator()(RationalPoint* const& a, RationalPoint* const& b) const {
return a->equals(*b);
}
UnRationalPoint::UnRationalPoint() {}
UnRationalPoint::UnRationalPoint(double a, double b) {
x = a;
y = b;
}
size_t double_hash::operator()(UnRationalPoint* const& a) const {
long long x1 = (long long) floor(a->x * 1e10);
long long y1 = (long long) floor(a->y * 1e10);
size_t a_hash = hash<long long>{}(x1);
size_t b_hash = hash<long long>{}(y1);
return a_hash * b_hash;
}
bool double_equal::operator()(UnRationalPoint* const& a, UnRationalPoint* const& b) const {
return fabs(a->x - b->x) < 1e-10 && fabs(a->y - b->y) < 1e-10;
}
下列函数为有理数顶点以及无理数顶点的定义,其中hash和equal为相应的重载接口。
附:改进
2020-03-15:参考博客后改进思路
借鉴点一:使用快速gcd函数对求最大公约数进行优化
引用博客中,博主在进行有理数化简求最大公约数时,使用了快速gcd的算法,具体算法代码如下:
ll fastGcd(ll x, ll y) {
if (x < y)
return fastGcd(y, x);
if (!y)
return x;
// 使用位运算以避免较慢的除法和取模
if ((x >> 1u) << 1u == x) {
// 两个偶数 或 一奇一偶
if ((y >> 1u) << 1u == y) return (fastGcd(x >> 1u, y >> 1u) << 1u);
else return fastGcd(x >> 1u, y);
} else {
// 一奇一偶 或 两个奇数
if ((y >> 1u) << 1u == y) return fastGcd(x, y >> 1u);
else return fastGcd(y, x - y);
}
}
//---------------------------
//以上代码引用自博客 https://www.cnblogs.com/FuturexGO/p/12457831.html
显然可以分析得到,该算法的时间复杂度最坏情况下和辗转相除法一致,最快可以达到\(O(logn)\),在题目中存在大量的直线,必然有大量的有理数点,因此该函数调用次数非常大,可以在一定程度上加快效率。
借鉴点二:坐标哈希函数
在本文中,本人的哈希函数设计思路是先将点坐标转换成字符串,再对字符串求哈希值。并且在效率分析中,指出了这种方式计算哈希函数会占用大部分的CPU时间,造成效率上的浪费。引用博文中作者采用的方式是参考自标准库中,对两个对象哈希值合并的一种算法。首先在计算效率上,会比笔者的方法要快得多(省去了转换字符串的不必要环节),并且算法参考自标准库,在效率上必然不会太差。因此可以进行改进。
借鉴点三:使用std::variant优化代码风格
参考博文中,作者提到:
后来通过查找资料,我在 这篇问答帖子 中找到了最佳的解决方案:使用std::variant和std::visit来优美地实现“多态二元函数”。
std::variant相当于一种升级版的union类型,可以安全地存储不同类型的对象,可以通过index()方法取得某对象的类型,也可以通过std::get(x)取得variant对象x的值。不仅如此,它还支持使用std::visit(visitor, vars)去自动处理各种类型为参数的函数调用(可以参考cppReference.com),正好和该问题的需求相匹配!其中,visitor是一个封装了callable函数的结构体,能支持每个参数的每种类型组合,vars是待传入的variant参数列表。
作者使用了variant对不同类型对象的存储做了优化,封装了两个不同的数据结构,将其化为一个,这样在一定程度上美化了代码,使得不那么冗余。



