P3371 【模板】单源最短路径 如题
- 时空限制1s / 128MB
题目描述
如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
输入输出格式
输入格式:
第一行包含三个整数N、M、S,分别表示点的个数、有向边的个数、出发点的编号。
接下来M行每行包含三个整数Fi、Gi、Wi,分别表示第i条有向边的出发点、目标点和长度。
输出格式:
一行,包含N个用空格分隔的整数,其中第i个整数表示从点S出发到点i的最短路径长度(若S=i则最短路径长度为0,若从点S无法到达点i,则最短路径长度为2147483647)
输入输出样例
说明
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=15
对于40%的数据:N<=100,M<=10000
对于70%的数据:N<=1000,M<=100000
对于100%的数据:N<=10000,M<=500000
样例说明:
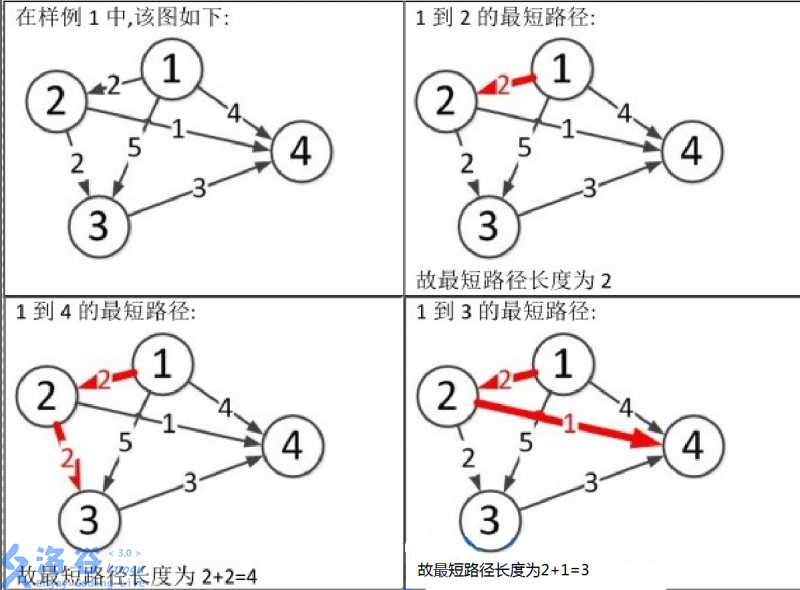
------------------------------------------------------------------------------------
SPFA模版:

1 #include<stdio.h> 2 #include<string.h> 3 #define maxn 500010 4 struct node{ 5 int to,next,w; 6 }; 7 node e[maxn]; 8 int dis[maxn],n,m,s,pre[maxn],cnt,tream[maxn]; 9 bool po[maxn]; 10 void spfa(); 11 void build(int,int,int); 12 int main(){ 13 scanf("%d %d %d",&n,&m,&s); 14 cnt=0; 15 for(int i=1;i<=m;i++){ 16 int a,b,c; 17 scanf("%d %d %d",&a,&b,&c); 18 build(a,b,c); 19 } 20 memset(po,0,sizeof(po)); 21 spfa(); 22 for(int i=1;i<=n;i++) printf("%d ",dis[i]); 23 return 0; 24 } 25 void spfa(){ 26 for(int i=1;i<=n;i++) dis[i]=2147483647; 27 int head=0,tail=1; 28 dis[s]=0;tream[tail]=s; 29 po[s]=1; 30 do{ 31 head++; 32 int o=tream[head]; 33 for(int i=pre[o];i;i=e[i].next){ 34 int to=e[i].to; 35 if(dis[to]>dis[o]+e[i].w){ 36 dis[to]=dis[o]+e[i].w; 37 if(!po[to]){ 38 po[to]=1; 39 tream[++tail]=to; 40 } 41 } 42 } 43 po[o]=0; 44 }while(head<=tail); 45 } 46 void build(int x,int y,int z){ 47 e[++cnt].to=y;e[cnt].next=pre[x];pre[x]=cnt;e[cnt].w=z; 48 }
------------------------------------------------------------------------------------
Dijkstra模版:

1 #include<stdio.h> 2 #include<string.h> 3 #define maxn 500010 4 struct node{ 5 int to,next,w; 6 }; 7 node e[maxn]; 8 int n,m,s,dis[maxn],pre[maxn],cnt; 9 bool po[maxn]; 10 void djs(); 11 void build(int,int,int); 12 int main(){ 13 scanf("%d %d %d",&n,&m,&s); 14 cnt=0; 15 for(int i=1;i<=m;i++){ 16 int a,b,c; 17 scanf("%d %d %d",&a,&b,&c); 18 build(a,b,c); 19 } 20 djs(); 21 for(int i=1;i<=n;i++) printf("%d ",dis[i]); 22 return 0; 23 } 24 void djs(){ 25 memset(po,0,sizeof(po)); 26 for(int i=1;i<=n;i++) dis[i]=2147483647; 27 dis[s]=0; 28 for(int i=1;i<=n;i++){ 29 int mi=2147483647,p; 30 for(int j=1;j<=n;j++) 31 if(!po[j]&&dis[j]<mi){ 32 mi=dis[j]; 33 p=j; 34 } 35 po[p]=1; 36 for(int i=pre[p];i;i=e[i].next) 37 if(dis[e[i].to]>dis[p]+e[i].w) 38 dis[e[i].to]=dis[p]+e[i].w; 39 } 40 } 41 void build(int x,int y,int z){ 42 e[++cnt].to=y;e[cnt].next=pre[x];pre[x]=cnt;e[cnt].w=z; 43 }
-------------------------------------------------------------------------------------
Dijkstra+优先队列优化:

1 #include<stdio.h> 2 #include<string.h> 3 #include<queue> 4 #define maxn 500010 5 using namespace std; 6 struct ppp{ 7 int dis,i; 8 bool operator < (const ppp& t)const{ 9 return dis>t.dis; 10 } 11 }; 12 struct node{ 13 int to,next,w; 14 }; 15 node e[maxn]; 16 int n,m,s,dis[maxn],pre[maxn],cnt; 17 void djs(); 18 void build(int,int,int); 19 int main(){ 20 scanf("%d %d %d",&n,&m,&s); 21 cnt=0; 22 for(int i=1;i<=m;i++){ 23 int a,b,c; 24 scanf("%d %d %d",&a,&b,&c); 25 build(a,b,c); 26 } 27 djs(); 28 for(int i=1;i<=n;i++) printf("%d ",dis[i]); 29 return 0; 30 } 31 void djs(){ 32 for(int i=1;i<=n;i++) dis[i]=2147483647; 33 priority_queue<ppp> que; 34 dis[s]=0; 35 ppp t;t.dis=0;t.i=s;que.push(t); 36 while(!que.empty()){ 37 t=que.top();que.pop(); 38 int u=t.i; 39 if(dis[u]!=t.dis) continue; 40 for(int i=pre[u];i;i=e[i].next){ 41 int to=e[i].to; 42 if(dis[to]>dis[u]+e[i].w){ 43 dis[to]=dis[u]+e[i].w; 44 t.dis=dis[to];t.i=to; 45 que.push(t); 46 } 47 } 48 } 49 } 50 void build(int x,int y,int z){ 51 e[++cnt].to=y;e[cnt].next=pre[x];pre[x]=cnt;e[cnt].w=z; 52 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号