福州大学算法作业题 - 游戏王

游戏王
★实验任务

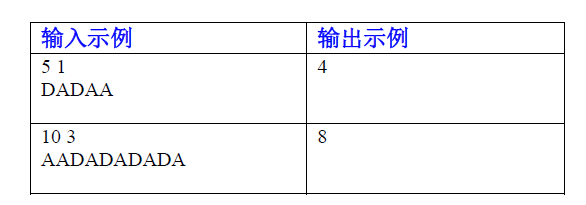
小茗同学又在玩游戏了一一Yu Gi 0h。

小茗同学目前有N只怪兽在场上，这N只怪兽排成一~排。每只怪兽有两个状态一一攻击状态(A)和防御状态(D)。

小茗同学手上有一张魔法卡，可以根据连续的状态一致的怪兽数量来恢复HP。在发动魔法卡前，小茗同学能改变最多M只怪兽的状态，即从攻击状态变为防御状态和从防御状态变为攻击状态。

由于怪兽的数量太多，小茗同学想让你帮他找出他能恢复HP的最大值。

 

★数据输入

第一行 输入两个整数 N, M ，分别表示怪兽数量和改变状态的数量。
第二行 输入一个长为 N的字符串，该字符串仅由 ’A’ 和’D’ 组成 （大写的 字母 A和字母 D）。

 

★数据输出 数据输出

输出小茗同学最多能恢复少 HP 。

 

★数据范围 数据范围

50 %的得分点， 1≤N≤100；
80 %的得分点， 1≤N≤200 0；
100 %的得分点， 1≤M≤N≤100,000 。

 

思路：

采用尺取法。

不是全部转化成A就是转化成D，然后取这两种情况中的最大值即可。用一个数组来存位置。

#include<iostream>
#include<string>
#define n 100000 
using namespace std;
int N,M,q[n];
string s;
int main()
{
    cin>>N>>M; 
    cin>>s;
    int  HP,head,tail,st;
    HP=head=tail=st=0;
    for(int i=0;i<N;i++)//改D
    {
        if(s[i]=='D') //如果是D
        {
            q[tail] = i;
            tail++;
        }        //记录第tail+1个D的位置
        if(tail-head>M) //如果改变的D的数量大于M
        {
            st=q[head]+1;
            head++;
        }        //最左边的D不改变，空出一个改变的次数
        if(HP<i-st+1)
        HP = i-st+1;
        if(HP>i-st+1)
        HP = HP; //此时的A串长度即为i-st+1
    }   
    head=tail=st=0;
    for(int j=0;j<N;j++)//改A ，同上
    {
        if(s[j]=='A'){
            q[tail] = j;
            tail++;
        }
        if(tail-head>M){
            st=q[head]+1;
            head++;
        }
        if(HP<j-st+1)
        HP = j-st+1;
        if(HP>j-st+1)
        HP=HP;
    }
    
    cout<<HP<<endl;
    return 0;
 }