广义串并联图方法学习笔记
最近不知道为啥突然蹦出一系列与之有关的题目们，特此记录一下。
理论
广义串并联图的概念被引入 OI 圈大概从 2019 的集训队论文《公园》一题开始。
不存在同胚于 \(K4\) 的子图的图被称为广义串并联图，这是一个比较抽象的概念。
常见的例如 树、仙人掌 等简单图结构都是广义串并联图。
广义串并联图拥有一系列性质：
-
去掉重边之后，\(m\leq 2n\)。
-
通过三种操作：删一度点，缩二度点，叠合重边。能够使得任意广义串并联图变为一个单点。
-
任何一个广义串并联图可以由如下的方式构造：初始只有一个点，每次可以选择：
- 加一个点，并和图中原有点连一条边。
- 选择两个直接相连的点，新加一个点与这两个点相连，并且可以选择是否删去原来连接这两个点的边。
也就是加入当前阶段的一度点或二度点。
-
广义串并联图是平面图。
对广义串并联图模型本身的更深入研究 或者 更多的理论本文将不再涉及。
个人认为更加宝贵的是 “删一度点，缩二度点，叠合重边” 这三个操作，称之为 “广义串并联图方法”。
实践
个人经验得出使用广义串并联图方法的最常见特征就是 \(m\leq n+k\)，其中 \(k\) 很小但 \(n\) 很大，例如 \(k=10,n\leq 10^5\)。
因为以上 \(3\) 种操作，无论 缩一度点（一换一）、缩二度点（一换二）还是叠合重边（零换一），\(m-n=k\) 的值都是不增的。
同时操作后所有点的度数 \(\geq 3\)，所以 \(2m\geq 3n\)，又有 \(m\leq n+k\)，得到 \(n\leq 2k,m\leq 3k\)。
于是 \(n,m\) 都到达了一个 \(O(k)\) 的量级，方便操作。
经典题
- 求给 \(n\) 个点 \(m\) 条边的无向图定向，使得其变为 DAG 的方案数。
- \(n\leq 10^5,m-n\leq 10\)。
首先当 \(n\leq 20\) 的时候是经典问题。
考虑枚举入度为 \(0\) 的一层，然后容斥，\(g(S)\) 表示 \(S\) 能否成为第一层，当且仅当 \(S\) 内部无边时为 \(1\)。
然后令 \(f(0)=1\)，那么有：
利用子集卷积能做到 \(O(n^22^n)\)。
根据套路使用广义串并联图方法，将图缩为 \(n\leq 20,m\leq 30\) 的样子。
边权的处理比较有技巧性，对每条边设 \((f,g)\) 表示它在某个方向上连通和不连通的方案数，每条边初始为 \((1,0)\)。
注意 \(f\) 没有钦定是哪个方向。
对于三种操作分开讨论：
- 删一度点：直接乘入答案，\(\text{ans}\gets \text{ans}\times(2f+g)\)。
- 缩二度点：
- \(f'=f_1\times f_2\)，想要连通需要两者均连通且方向一致。
- \(g'=g_1g_2+2g_1f_2+2f_1g_2+2f_1f_2\)，分别对应于：均断开，某一条边断开并钦定另一个方向，以及均不断开但方向相对或相反。
- 叠合重边：
- \(f'=f_1g_2+f_2g_1+f_1f_2\)，注意 \(f_1f_2\) 的系数唯一，两者不能相对，否则违背了 DAG 的定义。
- \(g'=g_1g_2\)，只有两者全断开才行。
最后先将 \(\prod(f_i+g_i)\) 乘进答案，然后在集合内部的必须是 \(g_i\) 断边，所以集合的权值为 \(\prod \dfrac{g_i}{f_i+g_i}\)，容斥方式则完全不变。
code
#include<bits/stdc++.h>
typedef long long ll;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define Ede(i, u) for(int i = head[u]; i; i = e[i].nxt)
using namespace std;
#define eb emplace_back
typedef pair<int, int> pii;
#define mp make_pair
#define fi first
#define se second
const int P = 1e9 + 7;
inline int plu(int x, int y) {return x + y >= P ? x + y - P : x + y;}
inline int del(int x, int y) {return x - y < 0 ? x - y + P : x - y;}
inline void add(int &x, int y) {x = plu(x, y);}
inline void sub(int &x, int y) {x = del(x, y);}
inline int read() {
int x = 0, f = 1; char c = getchar();
while(c < '0' || c > '9') f = (c == '-') ? - 1 : 1, c = getchar();
while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
return x * f;
}
int kpow(int a, int b) {
int s = 1;
for(; b; b >>= 1, a = 1ll * a * a % P)
if(b & 1) s = 1ll * s * a % P;
return s;
}
const int N = 2e5 + 20;
int n, m, ans = 1;
map<int, int> vec[N];
int cnt, f[N], g[N], deg[N], idx[N];
bool vis[N];
const int M = 20;
int edf[M][M], edg[M][M];
void solve() {
queue<int> q;
rep(i, 1, n) if(deg[i] <= 2) q.push(i);
while(! q.empty()) {
int o = q.front(); q.pop();
vis[o] = true;
if(deg[o] == 0) continue;
if(deg[o] == 1) {
pii u = * vec[o].begin();
vec[o].clear(), deg[o] = 0, vec[u.fi].erase(o);
ans = 1ll * ans * plu(plu(f[u.se], f[u.se]), g[u.se]) % P;
if(-- deg[u.fi] <= 2) q.push(u.fi);
}
else {
pii u = * vec[o].begin(), v = * (-- vec[o].end());
int a = u.se, b = v.se;
vec[o].clear(), deg[o] = 0, vec[u.fi].erase(o), vec[v.fi].erase(o);
g[a] = plu(plu(1ll * g[a] * g[b] % P, 2ll * g[a] * f[b] % P),
plu(2ll * f[a] * g[b] % P, 2ll * f[a] * f[b] % P));
f[a] = 1ll * f[a] * f[b] % P;
int k = vec[u.fi][v.fi];
vec[u.fi][v.fi] = vec[v.fi][u.fi] = a;
if(k) {
f[a] = plu(plu(1ll * f[a] * f[k] % P, 1ll * f[a] * g[k] % P), 1ll * g[a] * f[k] % P);
g[a] = 1ll * g[a] * g[k] % P;
if(-- deg[u.fi] <= 2) q.push(u.fi);
if(-- deg[v.fi] <= 2) q.push(v.fi);
}
}
}
int cnt = 0; rep(i, 1, n) if(! vis[i]) idx[cnt ++] = i; n = cnt;
rep(i, 0, n - 1) rep(j, 0, n - 1) {
int o = vec[idx[i]][idx[j]];
if(! o) edf[i][j] = edg[i][j] = 1;
else {
edf[i][j] = kpow(plu(f[o], g[o]), P - 2), edg[i][j] = g[o];
if(i < j) ans = 1ll * ans * plu(f[o], g[o]) % P;
}
}
}
void fwt(int* f, int opt) {
for(int o = 2, k = 1; o <= (1 << n); o <<= 1, k <<= 1)
for(int i = 0; i < (1 << n); i += o) rep(j, 0, k - 1)
if(opt == 1) add(f[i + j + k], f[i + j]); else sub(f[i + j + k], f[i + j]);
}
int cen[M + 1][1 << M], dat[M + 1][1 << M], val[1 << M];
int main() {
n = read(), m = read();
rep(i, 1, m) {
int u = read(), v = read(); cnt ++;
if(vec[u].find(v) != vec[u].end()) continue;
f[vec[u][v] = cnt] = 1, deg[u] ++;
g[vec[v][u] = cnt] = 0, deg[v] ++;
}
solve();
val[0] = 1;
rep(s, 1, (1 << n) - 1) {
int t = s - (s & - s), u = __builtin_ctz(s);
val[s] = val[t]; if(! val[t]) continue;
rep(v, 0, n - 1) if(t >> v & 1) val[s] = 1ll * val[s] * edf[u][v] % P * edg[u][v] % P;
int c = __builtin_popcount(s); cen[c][s] = (c & 1) ? val[s] : del(0, val[s]);
}
rep(i, 1, n) fwt(cen[i], 1);
dat[0][0] = 1;
rep(i, 1, n) {
fwt(dat[i - 1], 1);
rep(s, 0, (1 << n) - 1) rep(j, 0, i - 1) add(dat[i][s], 1ll * cen[i - j][s] * dat[j][s] % P);
fwt(dat[i], -1);
rep(s, 0, (1 << n) - 1) if(__builtin_popcount(s) != i) dat[i][s] = 0;
}
ans = 1ll * ans * dat[n][(1 << n) - 1] % P;
printf("%d\n", ans);
return 0;
}
「SNOI2020」生成树
- 给定无向图，保证去掉一条边后无向图是一棵仙人掌，求图的生成树个数。
- \(n,m\leq 5\times 10^5\)。
果断猜测无向图是广义串并联图，利用类似上一题方法设计边权为二元组 \((f,g)\) 分别表示断开与不断的方案数统计答案。
「JOI Open 2022」放学路
- 给定无向图，判断是否有 \(1\to n\) 且长度不等于最短路的简单路径。
- \(n\leq 10^5,m\leq 2\times 10^5\)。
根据部分分大力得到正解，一步步来。
首先对于 \(m\leq 40\) 可以搜索出所有路径，\(n\leq 18\) 直接状压，那么目光聚集于 \(m-n\leq 13\)。
不难条件反射出广义串并联图方法，之后 \(m\leq 3\times 13\) 同样可以搜索做，当然这一方法的作用不止于此。
首先先描述一下具体的缩合方法：
- 一度点就直接删，二度点的边权就直接相加。
- 叠合重边则需要注意：
- 如果重边的边权不同则将边权设置为不可到达，比如 \(-1\)（因为路径上显然不能包含这两个重边）。
- 否则就还是原权值。
- 同时还有特殊的一点，就是 \(1,n\) 即使度数 \(\leq 2\) 也不作为缩合对象。
自行想象一下 no 的情况，大概就是所有 \(1\to n\) 的简单路径们都缩到了 \((1,n)\) 这唯一一条边上，且边权不为 \(-1\)。
于是大胆断言答案为 no 当且仅当：缩合后 \(s\) 的唯一出边是 \((s,t,w)\)，且 \(w\neq -1\)。
当然这个猜测随便 hack，比如 Froggy 在 LOJ 讨论 里提到的 hack 长这样：
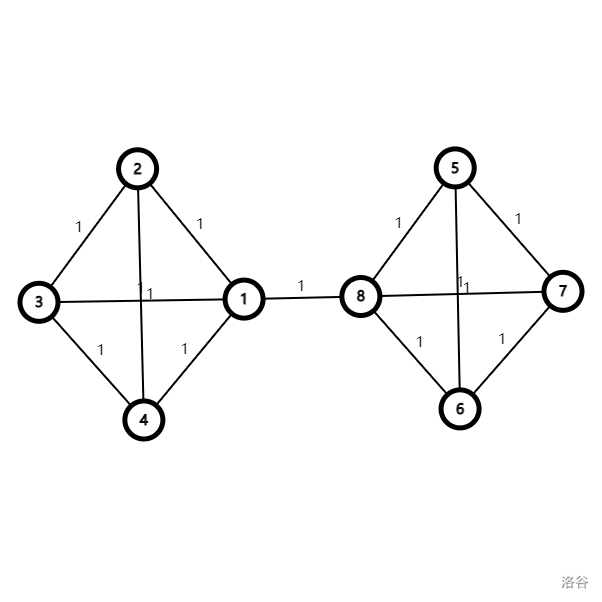
虽然这个 hack 看上去有些取巧，但是至少是个 hack，而且变相的更加使我们相信这个不靠谱的猜想有一定正确性。
再看一眼部分分，发现有：对于任意三座不同的城市 a, b, c，均存在一条从城市 \(a\) 到城市 \(c\) 且不经过城市 \(b\) 的路径 这个 sub。
翻译成人话就是整个图形成一个点双，同时不难发现上述 hack 的思路就是存在不同时包含 \(1\) 和 \(n\) 的点双。
那么难道说如果整张图是一个点双上述猜想就正确吗，实际上是这样的，证明如下：
此处证明参考官方题解并结合自己的一点思考，可以看作是本题最核心部分之一。
首先整理一下已知条件：整个图是点双联通的且所有点的度数 \(\geq 3\)。同时有点数 \(n\geq 4\)，否则无法满足度数均 \(\geq 3\) 的限制。
考虑将所有边定向，根据从 \(1\) 到它们的最短路，与最短路扩展方向同向定向。如果此时就有 \((u,v,w)\) 使得 \(\text{dis}(1,u)+w+\text{dis}(v,n)\neq \text{dis}(1,n)\) 的话那肯定是没救了。
否则定向后，称入度 \(>\) 出度的点为红色点，否则称为蓝色点。然后考虑 \(1\to n\) 的经过节点个数最多的简单路径，\(1\to a_1\to a_2\to \cdots\to a_p\to n\)。
首先得到 \(a_1\) 入度一定是 \(1\)，\(a_p\) 的出度一定是 \(1\)，否则一定能找到经过点数更多的路径。同时由于任意点度数 \(\geq 3\)，所以 \(a_1\) 一定是蓝色的，\(a_p\) 一定是红色的，换言之，路径一定经历了蓝红替换的过程。
考虑找到这样一条边，使得 \(a_i=u,a_{i+1}=v\)，且 \(u\) 为蓝色，\(v\) 为红色。根据定义，一定存在 \(u\to x(x\neq v)\) 以及 \(y\to v(y\neq u)\)，此时考虑路径 \(1\to y\to v\to u\to x\to n\)。除了 \(v\to u\) 之外，所有边任然需要根据定向移动。
如果它不是简单路径，不难发现只有可能是 \(x\to n\) 与 \(1\to y\to v\) 这段路径上有重合，不妨设第一个重合点为 \(x'\)。那么将原路径替换为 \(1\to u\to x\to z\to y\to v\to n\) 是经过更多点的选择，不符合定义。所以这条路径一定是简单的，且 \(>\) 最短路径的。
证毕
如此，所有非正解的部分分都有了解决方法。
当然更进一步也是容易的，因为如果从 \(1\) 出发进入一个以 \(1\) 为割点且不包含 \(n\) 的点双肯定是没有简单路径能到 \(n\) 的。
所以直接加一条 \((1,n,\text{dis}(1,n))\) 即等于它们之间最短路径的边，然后只考虑同时包含 \(1,n\) 的这个点双即可。
复杂度 \(O(m\log m)\)。
code
#include<bits/stdc++.h>
typedef long long ll;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define Ede(i, u) for(int i = head[u]; i; i = e[i].nxt)
using namespace std;
#define eb emplace_back
typedef pair<int, ll> pii;
#define mp make_pair
#define fi first
#define se second
inline int read() {
int x = 0, f = 1; char c = getchar();
while(c < '0' || c > '9') f = (c == '-') ? - 1 : 1, c = getchar();
while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
return x * f;
}
const int N = 1e5 + 10;
const ll inf = 1e16;
int n, m;
unordered_map<int, ll> g[N];
void add(int u, int v, ll w) {
if(g[u].find(v) != g[u].end()) {
if(g[u][v] != w) g[u][v] = g[v][u] = -1;
}
else g[u][v] = g[v][u] = w;
}
ll dis[N]; bool vis[N];
vector<pii> h[N];
ll getdis() {
priority_queue<pair<ll, int> > q;
rep(i, 1, n) dis[i] = inf;
dis[1] = 0, q.push(mp(0, 1));
while(! q.empty()) {
int u = q.top().se; q.pop();
if(vis[u]) continue;
vis[u] = true;
for(auto e : h[u]) {
int v = e.fi; ll w = e.se;
if(dis[v] > dis[u] + w)
dis[v] = dis[u] + w, q.push(mp(- dis[v], v));
}
}
return dis[n];
}
int dfn[N], low[N], stk[N], top, tim, cnt;
vector<int> scc[N];
void dfs(int u) {
dfn[u] = low[u] = ++ tim;
stk[++ top] = u;
for(auto e : h[u]) {
int v = e.fi;
if(! dfn[v]) {
dfs(v), low[u] = min(low[u], low[v]);
if(low[v] == dfn[u]) {
int o = 0; cnt ++;
do {o = stk[top --], scc[cnt].eb(o);} while(o != v);
scc[cnt].eb(u);
}
}
else low[u] = min(low[u], dfn[v]);
}
}
bool valid[N];
void build() {
n = read(), m = read();
rep(i, 1, m) {
int u = read(), v = read(), w = read();
h[u].eb(mp(v, w));
h[v].eb(mp(u, w));
}
ll cur = getdis();
h[1].eb(mp(n, cur));
h[n].eb(mp(1, cur));
dfs(1);
rep(i, 1, n) vis[i] = false;
int pos = 0;
rep(i, 1, cnt) {
for(int o : scc[i]) vis[o] = true;
if(vis[1] && vis[n]) {pos = i; break;}
for(int o : scc[i]) vis[o] = false;
}
assert(pos);
for(int o : scc[pos]) valid[o] = true;
rep(u, 1, n) if(valid[u])
for(auto e : h[u]) if(valid[e.fi]) add(u, e.fi, e.se);
}
queue<int> q;
void push(int u) {if(u != 1 && u != n && (int) g[u].size() <= 2) q.push(u);}
int main() {
build();
rep(i, 1, n) push(i);
while(! q.empty()) {
int u = q.front(); q.pop();
if(g[u].empty()) continue;
for(auto o : g[u]) g[o.fi].erase(u);
if((int) g[u].size() == 2) {
auto cur = g[u].begin();
int x = cur -> fi; ll a = cur -> se; cur ++;
int y = cur -> fi; ll b = cur -> se;
ll w = (a == -1 || b == -1) ? -1 : a + b;
add(x, y, w);
}
for(auto o : g[u]) push(o.fi);
g[u].clear();
}
if(g[1].find(n) != g[1].end() && g[1][n] != -1 && (int) g[1].size() == 1) puts("0"); else puts("1");
return 0;
}
