IOI2020国家集训队作业 Part 1
开坑!开坑!开坑!虐身虐心警告。
CF504E Misha and LCP on Tree
- 给定一棵树,每个节点有一个小写字母。
- 次询问,求路径 和 的 LCP。
- 。
直接 Hash,不要傻傻的写成两只 ,更不要直接套个二分 + 树剖三只 。
直接套用树剖结构,提取出 个区间,先区间相消,如果消不了了就在区间里二分,小常数单 。
CF505E Mr. Kitayuta vs. Bamboos
- 给定 个数 ,进行 轮操作,每次可以选择 个 进行 。
- 每轮操作后,会有 。
- 最小化最终的 。
- 。
二分答案改为每次给 个数加,逆向看是否能倒回 轮。
不要分步模拟这个过程,因为加减均有交换律,所以当直接枚举轮数,每次给“最紧急”的 个加,直接用堆维护。
如果中途都没了那就没了,否则最后还要让每个数能达到初始值。
CF506E Mr. Kitayuta's Gift
- 给定字符串 ,求在 中插入恰好 个小写字符使其变为回文串的方案数。
- 。
老神仙了。
第一步是要想到一个关于 的多项式的算法,也算是关键步骤了。
因为是回文串,所以两端应当一起考虑,先假设 为偶数。
令 表示填了首尾 对字符,前后尽量和原串匹配后,还剩下区间 的方案数。
设 表示用 对首尾能完全匹配的方案数,答案就是 。
转移需要讨论一下:
- :
- 若 , 和 。
- 若 , 和 。
- :
- 。
- 。
- 。
- 对 :。
为了去除 的影响,可以强行用矩阵加速这个 个状态的递推,复杂度为 。
发现这类转移能很好的表达到一张图上(来自官方题解):
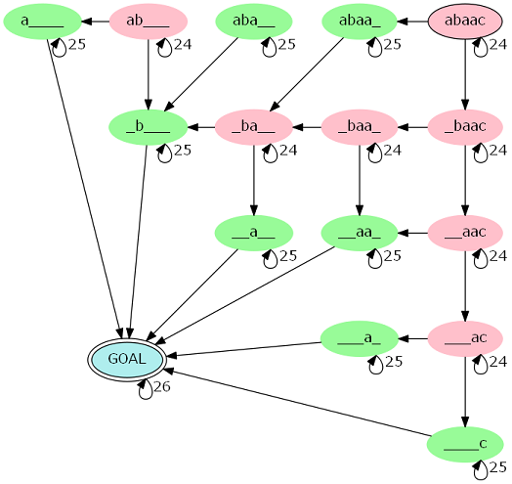
这是 的转移过程,红色和绿色分别对应 和 两种转移。
观察到上述转移中,红色点有 的自环,绿色有 ,蓝色对应的 则有全图唯一的 的自环。
同时不难发现,非自环边的权值都是 ,并且只能从绿色点到达目标点。
最终答案等价于从右上角出发,经过恰好 步到达目标点的路径权值之和,路径权值是途径权值的乘积。
将图片可视化之后,很快能发现,路径的具体形态不被关心,而是只关心路径上红色点( 的自环)和绿色点( 的自环)的个数。
而且能够发现,若一条路径有 个红色点,就一定有 个绿色点。
因为红色点的出边每次将区间长度 ,而绿色则大部分情况下 ,只在转移到终点时有特殊,所以要上取整。
综上,所有红色点个数相同的路径是本质相同的,可以利用这一点加速转移!
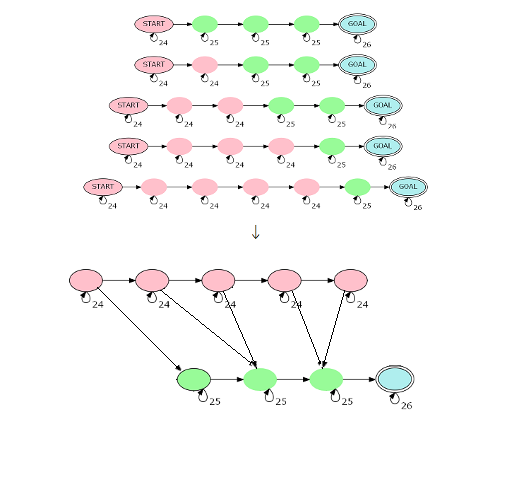
分别建立如上面第一张图的转移路径,每张只有 个点,而本质不同的路径也只有 个,直接矩阵转移就是 的。
当然要记搜预处理出 表示途径恰好 个红色点的转移路径数。
同时实际上发现这样做还是太傻了,可以直接上面一排红色点,下面一排绿色点,再在两排之间对应连边就好了,如上面的第二张图。
复杂度变为 ,而且转移形式是 DAG,所以转移矩阵是上三角矩阵,所以可以减少很多常数。
对于 为奇数的情况,把它当作 处理,再容斥掉一些情况即可。
需要容斥掉最后一次匹配不能填上当个字符的方案,发现就是只转移 且最终 没有多余匹配的方案。
无非就是把 重新计算,再把终点的自环去掉,再跑一遍即可。
CF512D Fox And Travelling
- 给定 个点 条边的无向图,一个点只有当它度数 时才能被删除。
- 对于每个 ,求有序删除 个节点的方案数。
- 。
发现对于一个环它永远无法被选择,需要考虑的只有有根树和无根树两种情况。
均可类似的使用树形 DP 解决,对于有根树的计算需要去重,钦定/换根/直接除法 都是不错的选择。
CF516D Drazil and Morning Exercise
- 给定一棵带边权的树,定义 。
- 次询问最大的满足 的连通块 的大小。
- 。
把直径提取处理画成一排,把子树挂在上面,十分形象。
发现每棵子树的 值都是随深度严格递增的,这一点非常有用。
根据连通块是否跨子树讨论,只在一个子树内非常好统计。否则考虑枚举连通块中的 ,它一定是某棵子树的根!
然后处理出这个根能扩展到的区间,因为递增性保证连通性,所以相当于二位数点,离线树状数组即可。
实际上 std 更简单,考虑双指针滑动一下,从大到小就不会影响连通性了,只是单点取消的时候在对应连通块 。
CF516E Drazil and His Happy Friends
- 有标号为 的 个黑点和标号为 的 个白点。
- 初始有 个黑点和 个白点是快乐的,其他都是不快乐的。
- 在第 天,编号为 的黑点会和 的白点联会,如果有任意一个快乐,那么联会后两者都会快乐。
- 求至少多少天能使所有人快乐,或者判定不可能。
- 。
妙妙数论题。
只想到了只有 的点对会在某个时刻联会。
实际上考虑直接按 分类,分别考虑答案,对于 的类,最终的实际贡献是 。
对于一类,如果初始没有开心的人就无解,否则一定有解。注意若 就一定无解,看似没用但实际保证了 是 级别的。
不妨设 ,首先特判掉在前 步就完成的情况。
否则只需要考虑左边 个点的开心时间,因为这样倒退 步,要么感染右边,要么被右边感染。
把右边初始开心的都对称到左边来,发现若左边 初始开心,他就会先感染右边的 ,并借此感染到左边的 。
那是否能视为**左边的 能感染左边的 **呢!
发现可以建图:
- 对于初始开心的点 ,连边 。
- 对于任意点 ,连边 。
跑最短路,最大值就是答案,可惜总点数过大,不能接受。
但是不难发现,第二种边将图连成了一个大环,而如果 和 这两个相邻节点初始均不开心,那么后者一定被前者感染。
换句话说前者就是不重要的,只需要保留初始开心的点,和它们在环上的前驱即可,这是 个的,就有保证了。
连边的时候有些技巧,就是对每个初始开心的点都建两个点, 表示自己, 表示自己的前驱。
然后连边 ,同时还需要找每个点在环上的相邻点,设 表示最小的满足 的值(可以用一次 exgcd 求出)。
那么两个点 的环上距离就是 ,固定一个起始点,求每个点到它的距离,排序就能得到在环上的相对顺序了。
注意是从 连边,对于的距离要 ,同时还要判断一下是否有 的情况,如果有就令两点连双向 边使之完全等价。
CF521D Shop
- 给定 个正整数 和 个操作 ,操作分为 种:
- 若 ,操作是 。
- 若 ,操作是 。
- 若 ,操作是 。
- 可以选择操作中至多 个,并按照一定顺序执行,求最大可能的 。
- 。
降智罚坐,被 IV 痛骂。
操作转 操作是简单的, 操作转 实际也不难,就是将 变为 。用一个堆贪心就行了。
CF521E Cycling City
- 给定一张无向简单图,问图中是否能找到两个点,使得两点之间有至少 条除端点外不交的简单路径。
- 。
降智罚坐,被 IV 痛骂 。
一直往点双想,实际上后来看到题解区有个结论:当且仅当一个点双恰为一个环时无解,否则一定可以构造解。
但是讨论巨大多。
实际上,一个更简洁而本质的结论为:若存在两个相交的环时一定有解,否则一定无解。充要都显然。
那么直接跑个 dfs 生成树,对返祖边差分覆盖,找到一个被覆盖 次的树边就直接构造即可。
CF526F Pudding Monsters
- 给定 的棋盘,共有 个棋子,且每行每列恰好一个。
- 求有多少 的子矩形中恰好有 个棋子。
- 。
这个是真的简单,不难发现 中的极大情况就是有 个,很直觉的就变成 了。直接分治。
CF526G Spiders Evil Plan
- 给定一棵带边权的无根树, 次询问,每次给定 。
- 要求选择 条树上路径(可交)构成一个包含 的连通块,且最大化连通块的边权和。
- ,强制在线。
发现一个有 个度数为 的点(叶子)的连通块(子树)能够被 条路径覆盖。
然后选择 个叶子到根的路径就是经典长剖 + 贪心,但是以每个点为根不能接受。
实际上,观察到最大的路径一定是该点到直径两端中的某个点,所以只用这两个点为根预处理。
注意直径端点一定是叶子,所以只有 可以用,唯一问题是如果前 条链不包含 怎么办。
再上贪心,无非两种情况:
- 去掉最后一条链换成 所在长链从底到上。
- 去掉 往上跳第一个到达的被选路径的一段,并改接为 所在的这段路经。
倍增预处理一下即可。
CF527E Data Center Drama
- 给定连通无向图,加尽量少的边,然后给边定向使得每个点的出入度都是偶数。
- 要求输出方案,可以有自环 / 重边。
- 。
比较刻意的构造,必要性探路。
每个点出入度都是偶数的必要条件是:作为无向图的时候,每个点的度数为偶数。
而这是无向图有欧拉回路的充要条件。
所以先将奇点配对连边,然后如果总边数为奇数再连一个自环,然后跑欧拉回路的同时,交替正负定向即可。
CF536D Tavas in Kansas
- 给定一张无向图,点有点权(可正负),边有边权。A 和 B 有各自的起点,两人博弈。
- A 先手,每次需要选择一个 ,将距离 A 的点都计入当前选手。
- 一个点不能被计入多次,如果全图的点均被计算了,那么游戏结束,得分高者获胜。
- 。
简单 DP,模型转化。
对每个点计算出到 A,B 的最短路,分别离散化后,令 ,即表达在网格图上。
每次 A 的选择是覆盖前几行,而 B 的选择是覆盖前几列。
用 表示覆盖了前 行,前 列,当前先手是 A/B 的 。
如果强行枚举当前先手覆盖的长度,复杂度是 的。
发现完全没有必要,因为转移过程本身就遍历了后续所有状态,不间断,所以只考虑 和 即可。
CF538G Berserk Robot
- 给出 个限制,形如 ,表示第 个单位时间机器人在 。
- 构造长度为 的 NSEW 序列,表示机器人按照这个序列循环不断移动,满足上述限制,或者判断无解。
- 。
虐心题,代码调一上午。
大概思路是求出每 次移动的 和 ,之后将每个限制变为 。
转化到一个循环里,对于新的 ,首先时间相同的限制要一样,其次满足两点:
- 。
- ,满足 。
这样每次就全力往某个方向走,多余的一定是偶数个,直接反复横跳即可。
关键是,如果不存在初始 相等的对,找到 和 并不简单。
于是转变思路,用上面的必要条件反向找可行的 和 。
对于奇偶性的限制,直接暴力枚举奇偶性,看是否可行即可。
对于不等式,将所有 都用上述方法转变为带未知元 的方程,把 等价拆为 。
然后就得到了一系列 和 的限制,枚举 ,根据另一限制和奇偶性找 即可。
CF538H Summer Dichotomy
- 给定 个区间,求将区间分为两部分,某一部分可以为空。
- 使得两部分区间分别有交,且交相加后与 有交。同时有 条两个区间不能在同一部份的限制。
- 。
妙妙题。
首先这题看着很 2-sat。先将 条边连接,跑二分图判定,得到黑白两个区间。
这样就相当于对每个连通块,它的两个区间必须分选,特别的,单点只有自己的区间 和 一个空区间,符合 2-sat 模型。
考虑限制,首先每部分区间有交,先把 和 拿出来。
-
如果 ,说明任意区间集合均有交,且都包含 。
只需要找一个 ,满足 属于某个区间,且 和 有交即可,并不难。
-
如果 ,两者必须分属两个部分。
但是这个思路后续似乎就不明朗了,看过题解后才发现应该直接贪心。
因为 和 是最松松松的限制了, 不能变小, 不能变大。
所以如果 就加 , 就减 ,然后就令两个点为最终决策点。
对必须选一个的跑二分图染色,不冲突即可。
CF547D Mike and Fish
- 给定平面内 个点,构造黑白染色使得对任意行或任意列,两颜色差的绝对值 。
- 。
经典题。
将点表达到边上,行列连边,得到二分图,将奇点统一连向一个虚点,这样图就有欧拉回路了。
对欧拉回路中,从左往右的染白,从右往左的染黑即可。
CF547E Mike and Friends
- 给定 个字符串。
- 多次询问 ,求 在 中出现了多少次。
- 。
论你写完题解后发现一道题的题解通道已关闭(
好像是没有人提出的做法。
因为 ,所以不同的 个数只有 种,这是经典根号分治。
也就是说,每个串中只有 个子串有贡献,这是可以接受的。
但是不能把这些子串都塞入 Hashtable 中,MLE 了。
但是也不难,直接将初始的 个字符串塞入 Hashtable 中,每次把子串的贡献加到 上(该子串与 相等)。
然后离线差分一下就没了,时间复杂度 。
小彩蛋:一开始写 unsigned long long 自然溢出的 Hash 被 hack 了,CF 果然名不虚传。
当然一开始就把所有串扔到 AC 自动机里去,离线标记 + 树状数组维护子树和也很经典了。
好像 SA + 二维数点也很经典了(这就是一套路满满题
CF553E Kyoya and Train
- 给定有向图,边有代价 和 个概率,分别表示经过这条边花费 个单位时间的概率。
- 如果在 时刻之后到达 ,需要交 元罚款。求最优决策下,从 的期望最小代价。
- 。
科技题。
一开始想了很久正着 DP,突然发现目标明确直接逆着 DP 就好了。
设 表示 时刻到达 ,从 还要花费的最小期望代价。
- 。
- 。(最短路)
- 。
然后直接差卷积 FFT,发现转移没有单调性,所以用 SPFA。看题解区据说复杂度并非 的,但是能过也不知道咋卡。
正解是分治 FFT,也不知道是啥科技(
CF555E Case of Computer Network
- 给定无向图,判断是否能将边定向使得给出的 对 都存在 的路径。
- 。
结论题。
老早就被灌输过一个 边双一定能定向为强连通分量 的结论,没想到还真能拿来出题。
直接边双缩点 + 给树上路径定向即可。实现时我还用了树上并查集,实际直接差分即可。
这个结论的证明:
考虑找到边双中任意一个环,并统一定向。
然后找到边 使得 在环中但 不在,如果找不到说明整个边双已经是强连通分量了。
然后就找到 到环,但是不经过 这条边的路径,并将这条链统一定向,融入视为“环”的一部分。
一定能成功,因为边双 至少有两条路径,也自然有 到环的路径。
CF559E Gerald and Path
- 给定 条线段,给出它的一个端点和长度,求所有线段覆盖的最大长度。
- 。
厉害题。
一开始的想法是:先将线段按给定端点排序,设 表示从前往后考虑到了 ,当前最右端是 , 的状态是往左/右。
然后转移的时候只考虑最右端点往右的贡献,因为(我认为),如果往左右贡献只能是完全包含先前线段,那还不如先前线段不被加入。
实际有严重问题,那就是先前线段可能有往右的贡献!!!
解决方法,同样的状态,类似的转移,但是当 的时候,还考虑 中最右端点 的贡献。
实际上很顺理成章的嘛,因为本身状态就这么设计的,连最右端的贡献都不计入怎么行(
只能说是核心思路想到了但实现出大问题。
CF566C Logistical Questions
- 给定一棵树,有点权边权。
- 的距离定义为 ,求树的带权重心。
- 。
不会求导ing
对于一类带权重心的经典解法就是调整法,每个时刻至多存在一条边,使得往该子树移动的带权重心减小。
原因是距离函数是下凸的,多个下凸函数的叠加还是下凸的。
问题是如何快速判断往哪个子树移动,之后可以用经典点分治多个 解决。
看式子,沿着边 移动的结果是:
如果往一个方向的函数值会减小,那么对它求导看哪个 即可,即观察:
的正负性。
CF566E Restoring Map
- 给定树上 个点的点集,各自的点集均由距离自己 的所有点构成。
- 并不知道每个集合对应哪个点,要求构造原树。
- 。
这种题目就是要 dfs 式的找性质。
发现距离为 的节点的交集大小恰好 ,且这两个点一定直接连边。
因此除了 (直接特判)的情况,所有非叶子节点直接的连边都能确定。
如果出现非叶子节点个数 的情况,不能通过集合区分叶子,但只会有两类叶子集合,分别挂在不同节点上即可。
否则对于叶子节点,能够确定它对应的集合,就是所有包含它的集合中,大小最小的一个。
要找到叶子的父亲,就是看只保留非叶子节点时,哪个集合与之相等。全程判断需要用 bitset 优化。
学会了遍历 bitset 的正确姿势:
for(int k = now._Find_first(); k != now.size(); k = now._Find_next(k))
CF568C New Language
- 将 开始的 个字符分为两个集合。
- 利用这 个字符构造满足 个限制的长度为 的字符串。还要求构造串的字典序不小于给定串 。
- 每个限制形如:若 上的字符 集合 ,那么 上的字符 集合 。
- 。
一眼 2-sat + 按位贪心。
CF568E Longest Increasing Subsequence
- 给定长度为 的序列,有 个空缺。给定 个数用于填补空缺。
- 输出严格上升子序列最大的方案。
- 。
考虑求严格上升子序列的 做法,维护的是当前长度为 的上升子序列的最小末尾。
在这里发现可以在每个空缺直接把 个数都插进去,因为严格上升代表转移不重。每次双指针就是 的。
个人认为最大难度在方案输出。
逆向构造是一定的,需要记录 表示 位置的上升子序列,非空缺能够直接记录个 。
空缺先看能否转移到非空缺,如果不能就贪心的用最大的一个数填补。
CF571D Campus
- 维护两类集合和一个序列,初始每类 个集合, 号集合下有且仅有 。支持 种操作:
U x y:将第一类中 所在集合合并。M x y:将第二类中 所在集合合并。A x:将第一类中 所在集合的下标在序列中均对应加上该集合大小。Z x:将第二类中 所在集合的下标在序列中均赋值为 。Q x:单点查询。
- 。
维护一个点加入集合的时间,就有一个显然的 的并查集做法了。
CF573E Bear and Bowling
- 给定长度为 的序列 ,求最大权值子序列 。
- 子序列的权值定义为 。
- 。
的 DP 式是很好得到的,之后就比较难动手,考虑了一会转移到网格图上。
然后突然发现转移的单调性,就是一定有一个位置,使得 之前的 是继承,之后的 是转移。
这样相当于需要在线维护 后缀加等差数列 和 单点查询。
这里我傻了,想了半天会了一个 平衡树 + 矩阵 的维护方法, 虽然更有普适性但是 1min 的时间真的不如写卡常的暴力(
实际上差分就变成后缀加了,每次查询前缀和即可 QwQ
CF575A Fibonotci
- 对于序列 ,,。
- 给定,之后有 个位置的 也给定,其余 。
- 求 。
- 。
一开始傻了不知道怎么用一个矩阵表示 个转移。实际上用 个矩阵即可……
对 个矩阵倍增预处理,对给定位置特殊处理即可。
实现上的一个细节是连续的给定位置会对矩阵有连续的影响,要同时考虑。
CF575E Spectator Riots
- 给定多个图形,每个图形中随机撒一个点。
- 在所有给定图形中找 个点,使得它们的外接圆期望覆盖的点尽量多。
- 如果有多个方案输出外接圆半径最大的,还有就任意输出。
- 。
题面是骗人的,实际一定存在覆盖所有图形的方案。
考虑一个无限大的圆不断缩小,直至接触到凸包上至少 个点。如果 个点不相邻那肯定移动到相邻覆盖范围更严格大。
所以感性理解以下在凸包上找 的相邻点的最大外接圆半径即可~
CF575I Robots protection
- 维护二维平面 ,支持两种操作:
- 加入一个两条直角边平行于坐标轴的等腰直角三角形。
- 询问一个点被多少个三角形覆盖。
- 。
直接做是 维偏序,不能通过。值域这么小显然是用来给二维树状数组的,所以目标是优化到 维偏序。
由于图形是对称的所以只考虑一种,发现可以简单容斥,如图:
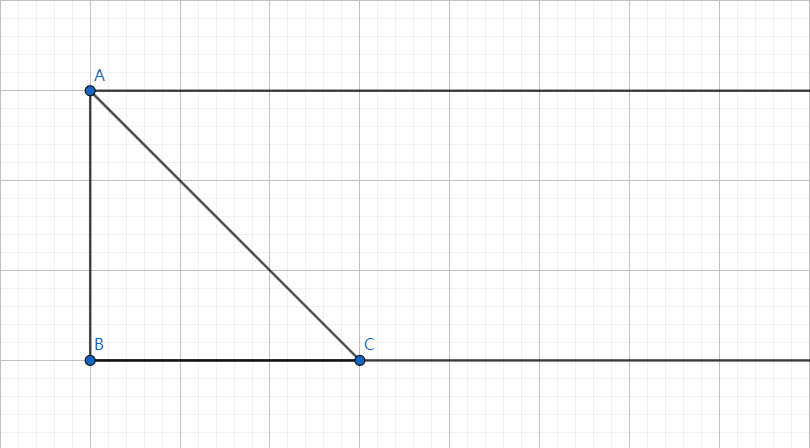
可以先把 以右的一个矩形 ()。
再把多余部分 ()。
其余几种也都是这种形式。
CF576D Flights for Regular Customers
- 给定一张 个点 条边的有向图。一开始在 号节点,要走到 号节点。
- 只有当你已经走过了至少 条边时,你才能走第 条边。
- 问最少要走多少条边,或判断无法到达。
- ,。
经典矩阵乘法,每次单边激活即可。
CF576E Painting Edges
- 给定一张 个点 条边的无向图。
- 一共有 种颜色,一开始,每条边都没有颜色。
- 定义合法状态为仅保留染成 种颜色中的任何一种颜色的边,图都是一张二分图。
- 有 次操作,第 次操作将第 条边的颜色染成 。
- 但并不是每次操作都会被执行,只有当执行后仍然合法,才会执行本次操作。
- 你需要判断每次操作是否会被执行。
- ,。
有些新意但是还是很板的线段树分治,可以看作是假的强制在线,按时间顺序走即可。
CF578E Walking!
- 给定长度为 的只包含
L或R的字符串 。 - 构造 的排列 满足 ,同时最小化 。
- ,保证数据有解。
中规中矩的构造题。
得到答案相对简单,维护所有候选集合,如果当前字符能够加到某个集合末尾就直接加,否则只能新开一个。
答案就是集合数 ,比较关键的是构造。
集合内部和构造无关,根据集合首尾定义 种集合:LL、LR、RL、RR。
首先让 LR 和 RL 们合并成至多一个自己种类,同时 LL 和 RR 拼接消耗。
注意因为一定有解,所以 LL 和 RR 两种导致一种字符比另一种多一个的在互相拼接消耗后,一定一共只剩下一个。
如果它此时存在的话就只需要将 LR 和 RL 分别拼接在两端。
否则只有一种情况比较棘手,那就是只剩下一个 LR 和一个 RL。
但此时根据讨论可以将一个串的开头放到另一个串的开头,从而形成 LL 和 RR 的局面,于是问题解决了。
CF582D Number of Binominal Coefficients
- 给定质数 和整数 ,求满足 且 的数对 的个数。
- 。
感觉像Kummer 定理这种的定理也就只能出现在数位 DP 中 QwQ
也就是说 中 的幂次等于 进制下 的进位次数,或者令 然后等价统计二元组 的个数。
设 表示考虑到了从高到低第 位,进位了 次,第 位是否进位, 是否顶到上界的方案数。
DP 的细节还是有的,有些系数甚至比较难推,举一例。
设 分别表示 第 位的数字,满足 ,求 ,即进位且受 的限制但之后 的方案数。有:
其它系数大概也就这个级别的推导,不过有 个……
CF582E Boolean Function
- 给定表达式,只有 八个
bool变量,且大小写字母相反。以及&和|两种操作符。 - 给定一个表达式,变量和操作符均可能是
?表示通配。 - 给定 组 表示当 取值如此时,表达式的值为 。
- 求合法的表达式个数。
- 。
建立表达式树,直接对 种状态状压,然后 fwt 维护转移即可,复杂度 。
CF585E Present for Vitalik the Philatelist
- 给定长度为 的序列 ,求二元组 的个数。 是一个包含 中整数的非空集合, 也是一个 的整数。
- 满足:,,。
- 。
一开始看错题了还想了挺久(
比较套路的拿 作容斥系数即可,每个数至多贡献 个 有值的位置,所以复杂度挺优秀的。
CF585F Digits of Number Pi
- 给定字符串 ,以及 位数 ,求有多少 且 有长度至少为 的子串是 的子串。
- 。
把 的所有长度为 的子串建立 ACM,直接数位 DP 即可。
CF587D Duff in Mafia
- 给定无向图,每条边有边权和颜色。
- 要求选出一组边,满足他们是一个匹配,且剩下的每种颜色的边也都构成匹配。
- 同时最小化选出的边权最大的边的边权,并输出。
- 。
盯了挺久没有思路的,属实是傻了。
首先二分答案,然后每个顶点至少选一条边,每种颜色每个顶点处也至多选一条边,不是显然的 2-sat 的模型吗!!!
在每个顶点处前后缀和以下应该是挺好些的。
实际上每种颜色的边们可以直接暴力建,因为如果一个顶点处有 条同色边一定无解嘛。
CF587F Duff is Mad
- 给定 个字符串,多次询问 在 中出现了多少次。
- 。
一眼看成 CF547E QwQ
那题我就是拿根号分治过的,这里思考了以下发现之前的思路并不可行了,然后逐渐自闭。
实际上还是考虑根号分治,根据 分类,设 。
-
对于 的:
因为这种串的个数很少,所以每次可以 。给 上的点标记,在 ACM 上预处理每个点的子树内的标记个数。
然后直接前缀和一下就能得到任意区间的答案了。
-
对于 的:
可以 就更简单了,考虑每个位置的贡献,只需要差分一下,每次 的子树 即可。
根号平衡一下能做到 子树加和 查询。
总时间复杂度 。
CF590E Birthday
- 给定 个字符串,保留尽量多的字符串,使得不存在一个字符串是另一个的子串。
- ,输出方案。
一眼根据 ACM 建立偏序集然后 Dilworth 最长反链,处理时只需要路径压缩。
需要注意的是当递归层数大到一定程度时,一定考虑递归栈的大小,例如这里 就一定不要写任何相关的 dfs。
然后人傻了不会 Dilworth 方案输出,编了好久网络流才猛然想起蓝书上都讲过……属实是基础不过关。
大体就是个调整法,一定有解什么的也挺好反证的。
传递闭包用 bitset 优化,如果匹配写个网络流的话,因为调整只需要 ,所以总时间复杂度是 (
CF603E Pastoral Oddities
- 给定一张 个点的无向图,初始没有边。
- 依次加入 条带权的边,每次加入后询问是否存在一个边集,满足每个点的度数均为奇数。
- 若存在,则还需要最小化边集中的最大边权。
- ,。
充要条件是所有连通块都有偶数个点,考虑经典 dfs 树构造。
至于最小化最大边权,只需要用考虑 Kruscal 的方式,不断按边权从小到大加入边即可。
考虑到动态加边,利用 LCT 维护最小生成树的方式(边化点然后维护链的边权最大值)。
用一个堆维护当前生成树内的边集,再利用 LCT 维护子树和那一套维护每个连通块点数的奇偶性即可……
听起来和写起来都挺 shit 的,算是 LCT 大融合了,为的就是那一只 QwQ
否则有一个可以完全和 LCT 无关的 分治 + 并查集的 两 做法。实测下来 LCT 的巨大常数完全打不过下面的好吧
CF605E Intergalaxy Trips
- 给定 个点的竞赛图,走过一条边需要一天,每条边每天出现的概率均为 。
- 保证 ,即可以在某个点等待。
- 求最优决策下 的期望天数。
- 。
显然是设 表示 的期望天数。
假设已知 的大小关系并将它们升序排序,那么每次的决策显然是从小到大选择第一个存在的边,同时如果 显然不如等待。
即:
移项得到最终结果:
问题是一开始只知道 ,其余点不知道。
其实只需要利用类似 的 Dijkstra 的思路,每次选择最小的 贡献给其余,动态维护每个未确定的 即可。
CF611H New Year and Forgotten Tree
- 给定每条边两端点 进制下的位数,构造对应的原树,或输出无解。
- 。
有点好玩,感觉这个 idea 很神奇。
想了很多基于贪心的构造,但实际上需要一个核心观察:
将每种位数取一个关键点,如果合法,总存在一种构造使得这些关键点构成一棵子树,其余点均挂在关键点下。
关键点只有 个,于是直接 枚举树的形态,然后就是一个二分图多重匹配。
CF613E Puzzle Lover
- 给定 的字母矩阵,同时给定长度为 的字符串 。
- 求有多少长度为 的有向路径,使得不经过重复格子,且按顺序构成了 。
- 。
发现如果路径回头就没救了,所以一定是两端一个 U 形,然后中间蛇形路线(
因为路径有向直接钦定从左往右走然后 reverse 再做一遍,注意当 时需要去重。
预处理 Hash 就能轻易得到左边的起始 U 形,中间则是简单的线性 DP,注意不重即可。
CF626G Raffles
- 有 种彩票,第 种有价值 ,别人已经买了 张。
- 你可以买 张彩票。假设第 种买了 张,需要满足 。
- 最大化 。
- 每次修改会有 ,保证时刻有 。
- 。
简单题。
静态的只需要一个堆维护 即可,因为这是个减函数。
修改时也很容易发现只需要将当前决策中最小的 不断拿出来比较即可,可以证明每次这样的修改都是 的。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· 三行代码完成国际化适配,妙~啊~
· .NET Core 中如何实现缓存的预热?
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?