JOISC 2014 简要题解
重新整理整个 JOISC 板刷的系列,在 CSP2022 之前当做复习。
同时以此纪念 2022 省选那段时间近似疯狂的刷题与飞速的进步,清淡的回忆。
「JOISC 2014 Day1」巴士走读
- 给定有向图 \(m\) 条边 \((u,v,s,t)\),每条边代表一条巴士路线,\(s,t\) 是发车和到达时间。
- 只有到达 \(u\) 的时间 \(\leq\) \(s\) 才能乘坐。
- \(q\) 次询问,求出如果要求时间 \(t\) 之前到达 \(n\) 号点,最晚什么时候出现在 \(1\) 号点。
- \(n,q\leq 10^5,m\leq 3\times 10^5\)。
对每个点来说,到达时间和出发时间显然是单调的,可以对每个点时刻维护这个单调序列。
具体来说,将所有边按照 \(t\) 升序排序并按顺序转移,这样能保证每次转移只会在单调序列的末尾加点。
每次在 \(u\) 的单调序列里二分即可转移,最终询问的时候也只需要在 \(n\) 的序列里二分。
复杂度 \(O(m\log m)\)。
「JOISC 2014 Day1」有趣的家庭菜园
- 给定序列,每次可以交换相邻两项,求最小交换次数。使得 \(\forall 2\leq i\leq n-1\),以下至少一个条件满足:
- \(\forall 1\leq j\leq i-1,h_j\leq h_i\)。
- \(\forall i+1\leq j\leq N,h_j\leq i\)。
- \(n\leq 3\times 10^5,h_i\leq 10^9\)。
转化一层,就是把序列变成单峰。
然后大力猜了个结论,结果直接过了,那就是:
尝试证明了以下,发现还真行。
- 必要性:设一个位置的权值为 \(\displaystyle \min(\sum_{j=1}^{i-1} [h_j>h_i],\sum_{k=i+1}^n [h_k>h_i])\),交换相邻两项,至多将较小数的权值 \(-1\)。而最终序列的权值为 \(0\),故答案至少为上式。
- 充分性:考虑按 \(h_i\) 从小到大,发现每次交换时,左右侧比它大的数,都是紧贴着它的连续一段。因为每次考虑到的小数都会被放到两侧。那么直接选择一路向左/右走即可。
还有一个不太需要偶发性结论的思考,假设已经得到了最终序列,那么最终代价就是初始序列到这个序列的置换排列的逆序对数。
从小到大考虑,发现小数不会对大数有影响,所以每次贪心的考虑往左还是往右的逆序对数少即可。
还是一样,因为从小到大考虑后每次比自己大的都是紧贴自己的连续一段,所以就是取两段长度的 \(\min\) 值。
「JOISC 2014 Day1」历史研究
- 给定长度为 \(n\) 的序列,\(q\) 次区间询问,求 \(v\times \text{cnt}_v\) 最大的 \(v\) 和 \(v\times \text{cnt}_v\),其中 \(\text{cnt}_v\) 表示 \(v\) 在区间中出现的次数。
- \(n,m\leq 10^5\)。
回滚莫队的板子题,感觉那个年代这种科技还是挺厉害的。
「JOISC 2014 Day1」拉面比较
- 交互题,用 \(\leq \frac{3}{2}n\) 次比较确定序列的 \(\min\) 和 \(\max\)。
- 交互库是自适应的。
一年 CSP-S 的初赛选择题。
可以相邻两数组合,先比较一次大小,然后大的和当前 \(\max\) 比,小的和当前 \(\min\) 比。
这也是理论下限了。
「JOISC 2014 Day2」水壶
- 给定 \(n\times m\) 网格图,其中有 \(p\) 个关键点。
- 其余格子有的是障碍,两关键点间距离为经过非障碍格的最短路,相当于以这种方式给出了关键点之间的完全图。
- \(q\) 询问求两点间最小瓶颈路径的瓶颈值。
- \(n,m\leq 2000,p,q\leq 2\times 10^5\)。
根据 Kruscal 的贪心过程不难发现瓶颈值就是最小生成树路径上的最大值。
问题是怎么把最小生成树建出来,并不能 \(O(p^2)\) 的求边。
其实也是简单的,从 \(p\) 个点同时开始跑多源 bfs,称一个格子被第一个到它的关键点管辖。
每次某个关键点尝试扩展时,如果该格子已经被管辖了,那么就在它与管辖该格子的关键点之间建边。
不难发现这样建图不会影响生成树,同时因为一个格子至多被从 \(4\) 个方向尝试扩展,所以边数是 \(O(nm)\) 的。
本质上,只是删去了那些存在 \(\max(\text{dis}(u,v),\text{dis}(v,w))\leq \text{dis}(u,w)\) 的 \((u,w)\) 边,显然不影响瓶颈树的建立。
「JOISC 2014 Day2」交朋友
- 给定有向图,反复执行操作:
- 如果存在 \(a\to b\) 和 \(a\to c\),连边 \(b\to c\) 和 \(c\to b\)。
- 直至没有新边出现,求最终图中的边数。
- \(n\leq 10^5,m\leq 2\times 10^5\)。
首先,把出度 \(\geq 2\) 的节点的所有出边到达的节点都缩到一起,它们的导出子图显然是完全图。
实际可以直接从所有被缩过的节点出发,在原图上 bfs,把能到的节点和自己缩一起。
因为如果自己被缩过,那么自己在一个完全图之中。所以只要有出边:
- 第一步,就会和完全图中的所有点(除了该点)连双向边。
- 第二步,就又会借助其它点连到该点。
相当于这个点也成为了完全图的一部分。
不能禁锢于简单的结论,有时需要考虑一定正确的更暴力的做法,可能时限并不会超。
大概这一类题目的思路就是找到一些简洁高效的性质。
「JOISC 2014 Day2」邮戳拉力赛
-
从车站 \(0\) 的上行站台出发,在 \(1\sim n\) 号车站均盖一个邮戳,再到车站 \(n+1\) 的上行站台结束。
-
求最短时间,两站之间无论上行下行都耗时 \(t\),而找台到邮戳台的时间则如图:
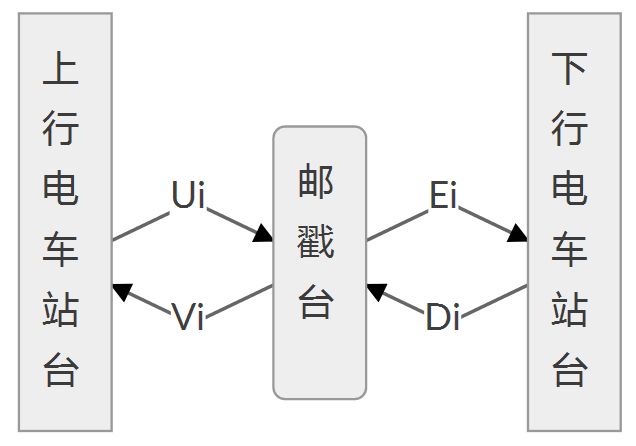
-
\(n\leq 3000,t,u_i,v_i,e_i,d_i\leq 10^5\)。
太妙了,读完题一点思路没有,感觉就像是什么人类智慧性质 DP 题。
先简单分析,发现一直往上走不优的情况,是因为可能可以先略过某个节点。
然后在上面的某个节点 \(u\) 进 \(e\) 出,绕一圈跑回来,到这里 \(d\) 进 \(v\) 出,再回去。
看似这个过程很复杂,但实际有性质:这样上下绕圈的节点对是可以匹配的,且一定是括号序。
根据贪心的想法,显然不可能存在非括号序的情况。
括号序有很好的性质,就像括号序列计数一样,可以记待匹配的左括号数,并把左右括号的贡献拆开 DP,从而快速转移。
可以设 \(f(i,j)\) 表示前 \(i\) 个车站,有 \(j\) 个 \(d\) 进 \(v\) 出的待 \([i+1,n]\) 的车站匹配的最小时间。
转移分挺多种:
- \(f(i,j)\gets f(i-1,j)+u+v\),就是正常经过。
- \(f(i,j)\gets f(i-1,j)+e+d(j>0)\),上面下来的时候顺路盖戳。
- \(f(i,j)\gets f(i-1,j+1)+u+e\),右括号。
- \(f(i,j)\gets f(i-1,j-1)+d+v\),左括号。
当然每次都要 \(f(i,j)\gets f(i,j)+2\times j\times t\),一次绕圈都要下去再回来。
但这还没有结束,因为第 \(i\) 个车站显然可能不会只做一次 左/右括号。
那显然不能平白无故给复杂度多个 \(n\),实际也很简单,直接按顺序同层转移即可。十分巧妙的括号序 DP 好题。
「JOISC 2014 Day3」JOIOJI
- 给定长度为 \(n\) 的字符集为
JOI的字符串,求最长的三种字符出现次数相同的字串长度。 - \(n\leq 2\times 10^5\)。
前缀和均同余的两个位置可以作为 \(l-1\) 和 \(r\),直接做就是了。
「JOISC 2014 Day3」稻草人
- 给定平面内 \(n\) 个点,求左下角是一个点,右上角是一个点,且中间没有点的矩形数。
- \(n\leq 2\times 10^5,x_i,y_i\leq 10^9\)。
比较简单,直接分治。
贡献计算的时候用了树状数组 + sort 排序,虽然理论 \(O(n\log n)\) 但是感觉常数巨大多。
实际有单调栈 + 归并排序的极小常数做法,也比较好想。
「JOISC 2014 Day3」电压
- 给定无向图(不保证连通,保证无自环,可能有重边),求满足以下条件的边数:
- 删去它之后整个图是二分图。
- 将剩下的图黑白染色后,存在方案使得这条边的两端节点同色。
- \(n\leq 10^5,m\leq 2\times 10^5\)。
有意思的结论题。
首先求 dfs 生成树,只考虑一条返祖边构成的环,一条树边合法,当且仅当:
- 所有奇环都经过这条边。这样能保证删完边后是二分图。
- 所有偶环都不经过这条边。保证所删边的两点同色。因为只有偶环上的点交替出现,且只有偶环有影响。
这就是充要了,一直担心的是有 \(\geq 2\) 条返祖边构成的简单环,但实际没必要:
- 两个偶环:显然都覆盖到自己影响的,不用重复覆盖。
- 两个奇环:构成了偶环,但实际奇环本身的覆盖就已经满足限制了。
- 一奇一偶:它就是讨论偶环不能经过这条边的原因,早已讨论到了。
所以直接做就完了,注意如果只有一个奇环,那么那条返祖边也是合法的,同时注意图不连通的情况。
「JOISC 2014 Day4」挂饰
- 给定 \(n\) 个挂饰,分别有 \(a_i,b_i\) 两个参数,代表它下面还能挂 \(a_i\) 个挂饰,它的价值是 \(b_i\)。
- 第一个挂饰可以挂在挂钩上,挂钩只有一个。最大化选择的挂饰的价值和。
- \(n\leq 2000,0\leq a_i\leq n,|b_i|\leq 10^6\)。
直接 DP,按 \(a_i\) 从大到小排个序即可,因为如果确定选的集合,那么先选 \(a_i\) 大的显然更可能挂得下。


