JOISC 2016 简要题解
「JOISC 2016 Day 1」俄罗斯套娃
- 给定 \(n\) 个套娃的直径 \(r\) 和高度 \(h\),只有直径高度均严格 \(<\) 的两个套娃才能套在一起。
- \(m\) 次询问 \((A,B)\),求对于所有 \(r\geq A,h\leq B\) 的套娃,至少需要套成几套。
- \(n,m\leq 2\times 10^5,r,h,A,B\leq 10^9\)。
这就是二维偏序集上的最小链覆盖,根据 Dilworth 定理即求最长反链的长度。
以每个点出发的反链恰好迎合的询问条件,可以直接排序后求最长非升子序列得到。
然后就是求所有 \(r\geq A,h\leq B\) 的 \(f(i)\) 的最大值,离线下来同样可以树状数组维护。
从图论角度考虑,把能比较的套娃连有向边,得到一个 DAG,本质就是要求最小不相交链覆盖。
对于一类特殊的 DAG,满足若 \(x\to y,y\to z\) 均有边,那么 \(x\to z\) 有边,就可以变为求最长链的长度。
实际上和偏序集的传递性定义是等价的,图论解释也比较优美。
「JOISC 2016 Day1」神经衰弱
- 有 \(2n\) 张牌,编号为 \([0, n-1]\) 各两张,每个编号有对应的等级,为一个 \([0,n-1]\) 的排列。
- 要求确定每个位置的牌的编号,每次询问形如 \((x,y)\),会位置 \(x,y\) 中,回答对应等级较低的牌的编号。
- \(n\leq 50\),限制询问次数为 \(300\) 次。
糊了个期望 \(O(n)\) 的分治,然后找了几个种子,19260817 过了(yyds)!
实际比较简单,考虑每次随机找一个点,然后问遍整个集合,它的编号显然是出现奇数次的那个。
然后所有与之不同的回答也都确定了那些位置的数。
每次将不确定的分治到下一次,注意选出的数的另一个相同数是确定不了的,放到下一次讨论即可,比较平凡。
每次期望下确定一半的数字,即 \(n+n/2+n/4+\cdots=O(n)\)。
找几个随机种子跑一下就那么过了。
「JOISC 2016 Day 1」棋盘游戏
- 有一个 \(3\times n\) 的棋盘,初始有一些棋子,可以任意顺序放置棋子,求合法的将棋盘放满的方案数。
- 一个放置是合法的,当且仅当放下每一个棋子前,以下两个条件至少满足一个:
- 它的左右都有棋子。
- 它的上下都有棋子。
- \(n\leq 2000\)。
很好的计数题。
有解的充要条件,显然是:初始四个角都有棋子,第 \(1,3\) 行初始没有连续两个空格。
那么此时 \(1,3\) 的格子可以在任意时候放置,只需要对第 \(2\) 行 DP 即可。
先考虑一个部分分:
初始时对于任意一个空格子,其上下左右相邻的空格子数不超过 \(2\) 个。
考虑将所有空格划分连通块,注意:
ooooooxoooooooxo ooooooxxxxxxxxxo ooooooooooooooxo中的连通块数不是 \(1\),而是 \(2\),因为初始 \(1,3\) 行都有棋子的列是可以直接忽略,当作填好的棋子单独考虑的,它可以在任意时候被放置。
那么实际每个连通块就很小了,不超过 \(3\times 3\) 的范围(记得要把最近的 \(1,3\) 都有的列划分进去)。
对于每个范围内的图形爆搜,然后每个连通块的方案组合一下即可。
考虑正解,将连续的第二行空格作为一个连通块考虑,最后组合起来。
设 \(f(i,j,0/1)\) 表示第 \(i\) 列,且中间格在前 \(i\) 列的空格中第 \(j\) 个放置,依靠的是上下/左右格子。
为了避免重复,若一个格子上下左右都有棋子,视为上下放置。
然后大概有 \(3\) 种转移,讨论一下,\(t\) 表示第 \(i\) 列 \(1,3\) 行的空格数:
-
第 \(i-1\) 和 \(i\) 列均是上下放置,无限制:
\[\displaystyle f(i,j,0)\gets t!\binom{j-1}{t}\sum_{j'} f(i-1,j',0) \] -
\(i-1\) 左右,\(i\) 上下,要求 \(i-1\) 在 \(i\) 之后放置:
\[\displaystyle f(i,j,0)\gets t!\binom{j-1}{t}\sum_{j'\geq j-t} f(i-1,j',1) \]其中 \(j-t\) 是根据插入 \(t+1\) 个数后,从更大的位置平移得到的。仔细思考 \(j\) 这一维状态的定义就不难得到。
-
\(i-1\) 上下,\(i\) 左右,要求 \(i\) 在 \(i-1\) 之后放置,且 \(i\) 的上下空格没有填满:
\[\displaystyle f(i,j+c,1)\gets \text{pos}(t,j-1) t!\binom{t}{c}\binom{\text{cnt}-j+1+t-c}{t-c}\sum_{j'\leq j-1} f(i-1,j',0) \]\(c\) 就是枚举在放置第 \(i\) 列之前有几个放置了,只能是 \([0,t)\)。
\(\text{cnt}\) 表示当前连通块中总空格数,不包括当前列的 \(t+1\) 个空格。
\(\text{pos}(x,y)\) 表示 \(x(x=0\ \text{or}\ x=1)\) 个棋子插入 \(y\) 个已放置的棋子的方案数,显然 \(x=0\) 时为 \(1\),\(x=1\) 时为 \(y+1\)。
然后注意每个连通块开始位置的初始化,这道题就做完了。
个人认为关键点是第二维状态的设计,后面是比较工业化的推导。
「JOISC 2016 Day 2」雇佣计划
- 维护长度为 \(n\) 的序列,\(m\) 次操作,支持:
- 单点修改。
- 求全局只保留 \(\geq V\) 的位置时,连续段的个数。
- \(n,m\leq 2\times 10^5,a_i\leq 10^9\)。
不难想到尝试在每一段的开头统计到这一段,即把相邻两个位置的数组成数对 \((a,b)\)。
那么就是统计 \(a<V,b\geq V\) 的数对个数,每次单点修改影响到至多两个数对,\(a_0=-\infty\) 即可。
就是动态二维偏序,于是我就无脑码了一个树套树,结果 \(\text{256MB}\) 直接裂开。(不过有积累到 \(10^5\) 的 \(O(n\log ^2 n)\) 空间必须至少 \(\text{512MB}\))
因为这里的询问特殊,可以考虑反过来,考虑每个数对会被哪些询问统计到,显然就是 \(V\in(a,b]\)。
用树状数组直接维护每种询问的答案即可……事实证明需要学会从代价计算的角度思考问题!
「JOISC 2016 Day 2」三明治
- 将网格图的每个格子按照 主对角线/次对角线 划开分成两半。
- 只有同时满足以下条件的三角形才不能被删除:
- 与它同一个网格的另一半三角形没有被删除。
- 至少有 \(1\) 个没被删除的三角形和它共直角边。
- 对每个格子,求把它里面的两个三角都删完,至少要删几个三角形。或者输出
-1。 - \(n,m\leq 400\)。
首先不难观察到,一个格子中的两个三角一定是同时被先后删除的。
也就是说,对于有解的格子,答案一定是偶数。(样例也应证了这个猜想)
然后,直接 \(O(n^2)\) 枚举每个格子,从它出发做 \(O(n^2)\) 的记忆化搜索,表示这个格子能否被删掉,就可以得到 \(O(n^4)\) 的做法。
具体细节的话,只需要考虑,主对角线划分的格子一定是 右上/左下 均空,次对角线类似。
实际上,每个格子被删时,它的 左/右 中至少有一个被删了,那直接对每一行同时统计,分别从左到右和从右到左搜。
每次保留上一次的结果就行了,时间复杂度 \(O(n^3)\)。
实现时需要控制这个格子被删的方向,行的转换可能会导致方向的变换。
因为转移不能成环,当然,如果这种情况下还是不可避免的成环了,那么这个格子无解。
「JOISC 2016 Day 2」女装大佬
- 有两种人排队换衣服,一种人只能用男换衣间,一种人两者皆可,且会优先使用女换衣间。
- 一共有 \(2n\) 个人(并不意味着两种人各占一半),给定方式是 \(m\) 个字符串和对应的重复次数,具体见原题输入格式。
- 按顺序更衣,如果一个只用男换衣间的人发现男换衣间被占用了,那么会让他后面第一个两者皆可的人进入女换衣间。
- 每个人换衣服都要 \(1\) 分中,要求一定要在时间 \(n\) 内所有人换完衣服,这可能意味着需要改变排队方式。
- 如果对于第 \(i\) 个人,原本 \(j\) 个排在他后面的人跑到他前面了,他的不满意度为 \(j\)。
- 最小化最大的不满意度。
- \(n\leq 10^{18},m\leq 10^5\)。
实际上比较简单的题目,但挺难转化的。
性质一:每一分钟两个换衣间一定都有人在使用。否则难以满足题目 \(n\) 分钟换完衣服的要求。
性质一推论:有解的充要条件是,将男士视为 \(+1\),皆可的人视为 \(-1\),任意后缀和 \(<2\)。
性质二:如果需要改变,一定是最后一位男士放到序列的最前端。反正改变了就会使一段后缀的不满意值 \(+1\),还不如所有人一起不满意。
不难发现,求的就是全局的最大后缀,简单写写就做完了。
「JOISC 2016 Day3」地牢 2
- 非常非常有趣的交互题。
- 有一个无向图,需要对于 \(\forall i\in[1,R]\) 回答最短距离恰好为 \(i\) 的点对数量。
- 这个无向图有 \(n\) 个点和 \(m\) 条边,\(n,m\) 不会告诉你。
- 初始你在某个房间,每个房间有一个宝石,初始所有宝石的颜色均为 \(1\),你只能进行如下操作:
- 询问当前房间的度数 \(d\)。
- 询问当前房间宝石的颜色。
- 选择一个编号 \(i\in[1,d]\) 并走这条边,同时离开前将宝石的颜色设置为 \(c\in[1,3]\)。
- 查询上一次走过的边在这个房间是几号边(用来回到上一个房间)。
- \(n,R\leq 200\)。仅对第三种操作有数量限制,必须 \(\leq 14m\),其中 \(m\) 是边数。
根据限制不难想到,应该是先给点标号后确定图的形态,再直接 \(O(n^2)\) bfs 得到答案。
题目最大的特点在于,只能通过宝石颜色来区分房间,注意到第四种操作很好的提供的 dfs 回头的过程,所以考虑无向图的 dfs 生成树。
未 dfs 过的点宝石颜色是 \(1\),当前点到祖先的链的颜色是 \(2\),已经 dfs 过的点则设为 \(3\),注意无向图 dfs 生成树只有返祖边的性质。
第一次 dfs 确定生成树的形态,并且在父亲处给儿子们标号,父子边也能确定下来。
之后对每个三进制位处理,在每个点的宝石处记录自己编号当前三进制位的值,这样返祖边也就能确定了。
总复杂度是 \(O(2(\log_3 n+1)m)\),最大为 \(12m\),能够通过。
「JOISC 2016 Day 3」回转寿司
- \(m\) 次询问 \((l,r,A)\)。每次执行:
for (int i = l; i <= r; i++) if(a[i] > A) swap(a[i],A);
- 输出每次的 \(A\)。
- \(n\leq 4\times 10^5,m\leq 25000\)。
实际上,每次就是把一段递增子序列平移,最大值扔掉。
考虑分块,发现对于整块,每次(如果能换)换出来的一定是最大值,所以用一个大根堆实时维护数字集合即可。
对于散块重构,对于新插入进当前块的数字集合用小根堆维护,对于堆顶,遇到的第一个 \(>\) 它的下标就是它被换到的位置。
同时记得将这个位置原先的值也放到小根堆中。这样就能完美维护这个过程了!
时间复杂度 \(O(q\sqrt n\log n)\)。
「JOISC 2016 Day 3」电报
- 给定内向基环森林,每个点可以改变它出边到的点,有对应代价。
- 求让所有点强连通的最小代价。
- \(n\leq 10^5\)。
就是求最大不相交链覆盖,而且因为是内向树,每条链就是直链。
每个点保留指向它的最大的边,如果整个环被保留就简单做一下就好了。特判整个图是个大环的情况。
「JOISC 2016 Day 4」危险的滑冰
- 在网格图中求从起点到终点的最小移动次数,一次移动会沿着直线直到某个障碍物前一格才停。
- 每次移动后,这次移动的出发点会出现障碍物。
- \(n,m\leq 10^3\)。
比较遗憾,实际上核心性质已经有了,但是连边那一步开始就想不到。
如果要到某个同行/同
列的格子,一定是反复横跳。
害怕的是需要记录新增的障碍物,可能除了这次横跳,以后还有用。
实际上担心是多余的,因为如果以后还有用到,那肯定不如这次到了那个被用到的格子后,直接换方向。
然后就可以连边,每个空格向四个方向连边,连出来大概长这样:
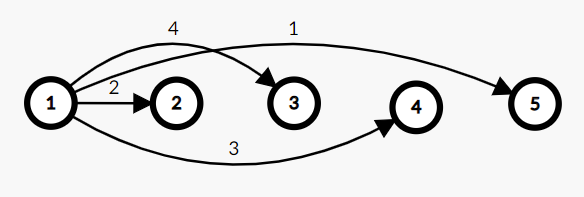
这是一个方向的连边,这样总边数是 \(O(n^3)\) 的,无法接受。
实际上,可以直接简化连边,容易发现这样和上面是等价的:
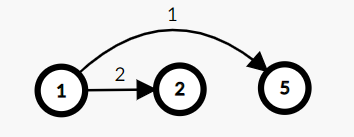
然后边权只有两种,用两个队列维护即可做到 \(O(n^2)\)。
「JOISC 2016 Day 4」最差记者 2
- 给定一场比赛中,中场和终场两次每个选手的国籍和成绩。
- 国籍变得混乱了,问要修改至少几个人在终场成绩中的国籍,才能使得表格符合国籍与中场对应,且每个人成绩不变少。
- \(n\leq 2\times 10^5\)。
实际上是一个匹配,匹配尽量多的人,使得剩下的存在任意修改变得合法的方案。
按照成绩将两部分混合起来排序,匹配很贪心,终场点选择最近的和自己国籍相同未被匹配的中场点的即可。
剩下的点相当于是问二分图是否有完备匹配,很难不想到 Hall 定理。
这个图很特殊,每个点是向一段前缀连边,故一个点集的出边能到达的点集大小,就是最大点的出边个数。
而要尽量使得 Hall 不满足,显然这个点集也应当选择一段前缀。
故很自然的,若将中场点变为 \(+1\),终场点变为 \(-1\),就是指去掉匹配点之后,要求任意前缀 \(\geq 0\)。
用线段树不难判定这个过程,容易发现能匹配就匹配是正确的。


