斜率优化学习笔记
【前言】
斜率优化是经典的对 1D/1D 动态规划模型的决策单调性优化。
对于这样的 DP 方程:\(f(i)=min_{1\leq j<i}\{f(j)+valid(i,j)\}\)。
可以发现暴力是 \(1\) 维状态 \(O(n)\) 转移,我们可以考虑决策单调性相关优化。
- 若 \(valid(i,j)\) 中只包含关于 \(i,j\) 的项相互独立,可以考虑单调队列优化。
- 若 \(valid(i,j)\) 中包含 \(i,j\) 的乘积项,可以考虑斜率优化。
- 若 \(valid(i,j)\) 满足四边形不等式,可以考虑更具有普适性的四边形不等式优化,支持扩展至二维。
本文着重介绍 \(2\)。
【主要思想】
以任务安排 3为例。
首先预处理前缀和,不难写出状态转移方程:
然后将 \(\min\) 符号略去,将方程尽量展开,让所有数据便于分类:
我们可以将数据分为 \(3\) 类:
- 只与 \(i\) 有关的项。
- 只与 \(j\) 有关的项。
- \(i,j\) 的乘积项。
如果出现更加复杂的情况,可能斜率优化就不再适用了。
通常我们将 \(2\) 移动到等式左边,\(1,3\) 移动到等式右边,目的之后再说。
先看看形式:
可以发现这个柿子很像我们学过的一次函数:\(y=kx+b\)。
解决数学问题时,将问题转化到图像上往往是一个更加直观且高效的方法,OI 中也一样。
我们可以看看转化形式:
- \(y=f(j)\)。
- \(k=sumT(i)+S,x=sumC(j)\)。
- \(b=f(i)-sumT(i)\times sumC(i)-S\times sumC(N)\)。
通常我们将 \(j\) 的相关项作为变量(也就是 \(x,y\)),这与 \(j\) 是未定的决策的事实是相吻合的。
看看我们的目标 \(f(i)\),它当然身处 \(b\) 中(它显然只与 \(i\) 有关,属于分类 \(1\))。
更容易发现的是,\(b\) 中的其它项皆为与 \(i\) 有关的项或常数项。
也就是说,无论 \(j\) 如何取值,\(b\) 始终不发生改变,而我们的目标是令 \(b\) 尽量小(这样 \(f(i)\) 才尽量小)。
利用上面的 \(x,y\),将前面所有的决策 \(0\leq j<i\) 看做 \(i\) 个点 \((x,y)\),我们就是求使 \(b\) 达到最小的点。
那么什么点能够符合要求呢,显然是将一条斜率为 \(k\) 的直线从下自上平移,第一个碰到的点即为所求。
显然平移的时间越短,\(b\) 也就越小,\(f(i)\) 也就越小。
以上是斜率优化的主要思想,至此,我们已经成功了一半。
之后,我们需要模拟直线向上平移的过程,这是一个难点。
仔细画图分析一下
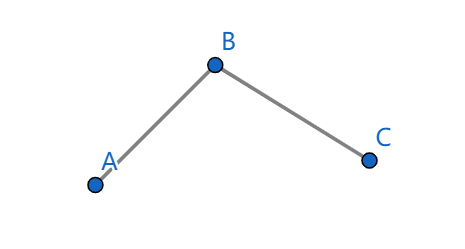
对于上面这种情况,无论以何种斜率从下至上平移,\(B\) 点都不可能是首先被达到的。
所以我们就可以直接排除掉它了。
更近一步发现,我们需要维护的,是这样一个形状:
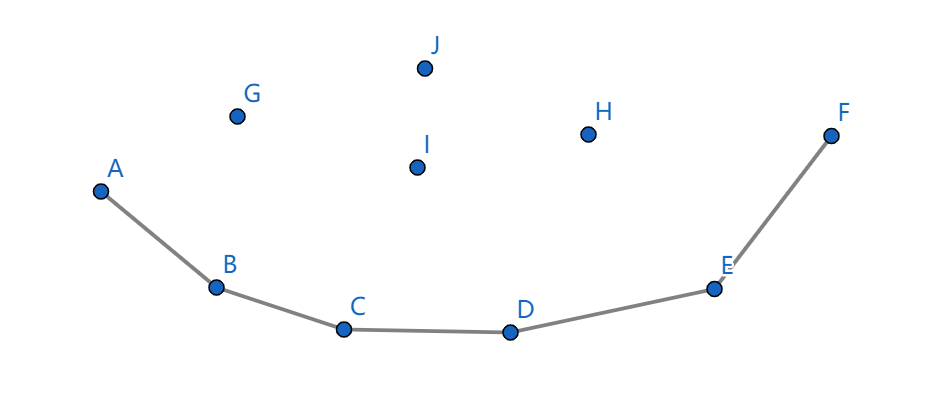
而对于 \(G,H,I,J\) 点来说,它们已经不会对答案有任何贡献了。
我们需要维护的是这个向下凸的形状,我们称之为下凸壳。
不难发现这里的 \(x\) 是单调递增的,也就是说我们每次在凸壳的左右端尝试插入新的决策。
那么利用一个队列,每次如果出现如图 \(1\) 的形状就将队尾删除,然后加入新点即可。
有些简单的斜率优化题目,\(k\) 也是单调的(例如本题的弱化版:任务安排 2)。
那么显然只要每次在队头及时删除即可,更具体点,若队头两点的斜率 \(\leq k\),那么删除队头。
对于本题而言,\(k\) 并不单调,也就是说虽然队头这次可能没用,但是之后可能作为最优决策。
所以不能进行删除,那么就可以在队列上二分,找到第一个斜率 \(>k\) 的相邻两点即可。
时间复杂度 \(O(n\log n)\)。
【代码实现】
至此,斜率优化的思想已经全部结束了。
斜率优化的代码往往不长,但是队列中斜率的比较往往看上去“令人窒息”。
实际上只要自己愿意写柿子,将所有算式都在纸上写好,实现时思路将会非常清晰。
值得注意的是,为了防止精度损失,往往利用交叉相乘将斜率比较时的除法变为乘法。
当然有的人的写法是利用 long double 尽量避免精度损失,但是同时会带来不必要的讨论。
所以这里推荐写法一,下面是参考代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 300010;
typedef long long LL;
int n, S, l = 1, r = 1;
LL sumt[N], sumc[N];
double f[N];
int q[N];
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
int Find(int i){
int L = l, R = r;
while(L < R){
int mid = (L + R) >> 1;
if(f[q[mid + 1]] - f[q[mid]] <= (sumc[q[mid + 1]] - sumc[q[mid]]) * (S + sumt[i])) L = mid + 1;
else R = mid;
}
return q[L];
}
int main(){
n = read(), S = read();
for(int i=1; i<=n; i++){
int t = read(), c = read();
sumt[i] = sumt[i - 1] + t;
sumc[i] = sumc[i - 1] + c;
}
q[1] = 0;// 注意是有 0 决策的,所以初始化队列要加入 0 好决策,也就是点 (0,0)。
for(int i=1; i<=n; i++){
int now = Find(i);// 二分寻找最优决策。
f[i] = f[now] - sumc[now] * (sumt[i] + S) + sumc[i] * sumt[i] + S * sumc[n];
while(l < r && (f[q[r]] - f[q[r - 1]]) * (sumc[i] - sumc[q[r]])
>= (f[i] - f[q[r]]) * (sumc[q[r]] - sumc[q[r - 1]])) r --;// 在队尾维护凸壳。
q[++ r] = i;// 加入新决策。
}
printf("%.0lf\n", f[n]);// 使用 double 的原因是答案可能会爆 long long。
return 0;
}
【做题经验】
首先你要判断一道题是否能够使用斜率优化,不论如何,首先要正确地推出暴力的初始 DP 方程。
然后是对于维护凸壳时的几种情况:
- \(x,k\) 都单调递增,使用队列维护即可,时间 \(O(n)\)。
- \(x\) 单调递增,\(k\) 不单调,任然使用队列维护凸壳,二分寻找最优状态即可,时间 \(O(n\log n)\)。
- \(x\) 不单调,\(k\) 单调递增,考虑倒序 DP,此时方程中 \(x,k\) 中的项往往会“交换”,变为情况 \(2\)。
- \(x,k\) 都不单调,需要满足任意位置插入任意位置查询,可以使用平衡树维护。
对于 \(4\),可能更方便的是使用 CDQ 分治离线处理,这个后文会提及。
我们是以下凸壳为例,当然了,对于某些最大化问题,我们需要从上往下平移直线。
类似的,我们需要维护一个上凸壳,操作都是类似的,不再赘述。
最后是一些容易写错的点:
- 初始化,特别是队列的初始化,如果有 \(0\) 点就加入 \(0\),否则令 \(l=1,r=0\),表示没有数。
- 细节,例如容易爆 int 的地方要使用 long long,以及方程不要写错。
- 比较斜率时推荐使用叉积的方法,比较时注意是
<=,方便去重。
【简单习题】
【情况1】
对应上面的讨论,\(x,k\) 都单调。这种情况最简单。
将一个单调不减的整数序列 \(A\) 分为若干段,使得每一段的长度 \(\geq k\)。
每一段的代价为段中所有数与最小数的差的和,求代价最小值。
注意题意是经过转化的,利用了贪心思想进行分段,读者可以自己尝试证明。
设 \(f(i)\) 表示将前 \(i\) 个数按照规则分段的最小代价,预处理前缀和,显然有方程:
利用上面的技巧可以快速转化方程,然后直接利用斜率优化求解即可。
值得注意的是,这里的 \(0\leq j\leq i-k\),所以 \(i\) 可以直接从 \(k\) 开始,每次结束后将 \(i-k+1\) 加入队列。
#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
using namespace std;
const int N = 500010;
const int INF = 1e12;
int T, n, k, a[N];
int q[N * 2];
int f[N], sum[N];
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
int Get_Y(int j){
return (f[j] - sum[j] + a[j + 1] * j);
}
signed main(){
T = read();
while(T --){
n = read(), k = read();
for(int i = 1; i <= n; i ++){
a[i] = read();
sum[i] = sum[i - 1] + a[i];
}
for(int i=1; i<=n; i++) f[i] = INF;
f[0] = 0;
int l = 1, r = 1;
q[1] = 0;
for(int i = k; i <= n; i ++){
while(l < r && Get_Y(q[l+1]) - Get_Y(q[l])
<= (a[q[l+1] + 1] - a[q[l] + 1]) * i) l ++;
f[i] = f[q[l]] - a[q[l] + 1] * (i - q[l]) + sum[i] - sum[q[l]];
int now = i - k + 1;
while(l < r && (Get_Y(q[r]) - Get_Y(q[r-1])) * (a[now + 1] - a[q[r] + 1])
>= (Get_Y(now) - Get_Y(q[r])) * (a[q[r] + 1] - a[q[r-1] + 1])) r --;
q[++ r] = now;
}
printf("%lld\n", f[n]);
}
return 0;
}
稍微复杂一点点的推柿子,其实是裸的模板题。
推完柿子后照样是裸的斜率优化,但是这次是最大化问题。
所以维护上凸壳,\(k\) 又是单调递减,所以在队尾取得答案,可以发现所有操作都是在队尾。
于是这里本质上是利用栈求解,其实更简单了。
【情况4】
关于情况 \(2,3\) 的例题,就留给读者自己寻找了。
主要讲解一下都不单调时的 CDQ 分治解法。
主要思想是既然你不单调,我就离线构造出单调的情况,进行求解。
常见套路:
- 将数据读入,直接将 \(x,k\) 处理出来。(这里的 \(x\) 是 \(i\) 作为决策时的 \(x\),\(k\) 是 \(i\) 作为询问时的 \(k\))
- 将数据按照 \(k\) 单调递增排序。(目的是构造出询问递增的情况)
- CDQ 分治内部,首先按照 \(i\) 递增排序,保证决策 \(j<i\),然后递归处理 \((i,mid)\)。
- 处理完左区间后,保证左区间 \(x\) 单调递增,右区间 \(k\) 单调递增,转变为情况 \(1\) 统计左区间对右区间的贡献。
- 递归处理 \((mid + 1, r)\)。
- 将左右区间合并,按照 \(x\) 单调递增排序。(这是 \(4\) 的前提)
- 对于终点状态 \(l=r\) 的情况,此时 \(f(l)\) 的答案必定已经统计完毕,直接统计 \(y\) 即可,方便之后的斜率比较。
注意所有排序都是利用归并排序,保证 \(O(n\log n)\) 的分治复杂度。
同时,每次状态转移不能只接赋值,因为每次并没有考虑所有决策(而是左区间对右区间的)。
这也启示我们要像一般的 DP 一样,注重初始化。
或许结合例题能有更加深刻的理解。
设 \(f(i)\) 表示让 \(1\) 和 \(i\) 连通的最小花费,预处理 \(w\) 的前缀和,同一得到方程:
常规拆柿子之后,发现 \(x,k\) 均没有单调性,所以使用 CDQ 离线求解即可。
可能关键是代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N = 100010;
const LL INF = 1e18;
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
int n, h[N], q[N];
LL sum[N], f[N];
struct node{
int x, k, id;
LL y;
} a[N], b[N];
bool cmp(node a, node b){return a.k < b.k;}
#define X(i) a[i].x
#define Y(i) a[i].y
void solve(int l, int r){
if(l == r){
int j = a[l].id;
a[l].y = f[j] - sum[j] + 1LL * h[j] * h[j];
return;
}
int mid = (l + r) >> 1;
int t1 = l, t2 = mid + 1;
for(int i = l; i <= r; i ++)
if(a[i].id <= mid) b[t1 ++] = a[i];
else b[t2 ++] = a[i];
for(int i = l; i <= r; i ++) a[i] = b[i];
solve(l, mid);
int head = 1, tail = 0;
for(int i = l; i <= mid; i ++){
while(head < tail && (Y(q[tail]) - Y(q[tail - 1])) * (X(i) - X(q[tail]))
>= (Y(i) - Y(q[tail])) * (X(q[tail]) - X(q[tail - 1]))) tail --;
q[++ tail] = i;
}
for(int i = mid + 1; i <= r; i ++){
while(head < tail && (Y(q[head + 1]) - Y(q[head]))
<= 1LL * a[i].k * (X(q[head + 1]) - X(q[head]))) head ++;
if(head <= tail){
int id = a[i].id, j = q[head];
f[id] = min(f[id], a[j].y - 1LL * a[j].x * a[i].k + sum[id - 1] + 1LL * h[id] * h[id]);
}
}
solve(mid + 1, r);
t1 = l, t2 = mid + 1;
int tot = l - 1;
while(t1 <= mid && t2 <= r)
b[++ tot] = (a[t1].x < a[t2].x || (a[t1].x == a[t2].x && a[t1].y < a[t2].y)) ? a[t1 ++] : a[t2 ++];
while(t1 <= mid) b[++ tot] = a[t1 ++];
while(t2 <= r) b[++ tot] = a[t2 ++];
for(int i = l; i <= r; i ++) a[i] = b[i];
}
int main(){
n = read();
for(int i = 1; i <= n; i ++){
h[i] = read();
a[i].x = h[i];
a[i].k = 2 * h[i];
a[i].id = i;
}
for(int i = 1; i <= n; i ++){
int w = read();
sum[i] = sum[i - 1] + w;
f[i] = INF;
}
sort(a + 1, a + n + 1, cmp);
f[1] = 0; solve(1, n);
printf("%lld\n", f[n]);
return 0;
}
一定要拿出来强调的是第 60 行归并排序 \(x\) 时的这句话。
a[t1].x < a[t2].x || (a[t1].x == a[t2].x && a[t1].y < a[t2].y
为什么这么写呢,因为当 \(x\) 相同而 \(y\) 不同时,显然选择 \(y\) 最小的是最优的。
然而我们利用叉积比较时,如果有连续 \(3\) 个 \(x\) 的相同,会导致不等式两边必定为 \(0\)。
也就表示不等式一定成立,也就是说除了第一个决策,后来的决策一定会“挤”掉先来的决策。
这就代表除非我们将最小的 \(y\) 放在最前面,否则它将有被挤掉的风险。
所以这个判断是保证正确性的必须判断。
当然如果你使用 long double + 除法 的比较方法,相应的讨论就是 \(x\) 相等时斜率赋 -inf 还是 inf 的问题。
【总结】
斜率优化是经典的动态规划优化技巧。
如果你有兴趣更加深刻的理解它,推荐看看这篇文章的前几个部分。
更多习题同样可以在那篇文章的末尾找到。
完结撒花。

