Johnson 算法学习笔记
前言
Johnson 和 Floyd 一样是用来解决无负环图上的全源最短路。
在稀疏图上的表现远远超过 Floyd,时间复杂度 \(O(nm\log m)\)。
算法本身一点都不复杂(前提是你已经掌握了多种最短路算法),而且正确性很容易证明。
注意:全文多处引自SF dalao 的文章。
再次注意:模板题贴在这里,请熟读题面再看代码。
引入
想想求一个有 \(\leq 3000\) 个点和 \(\leq 6000\) 条边的有负权图的全源最短路,你发现 Floyd \(O(n^3)\) 爆体而亡。
那怎么办办呢...,我们先假设没有负权,然后可以想到一下很暴力的做法:
既然没有负权我们可以用 \(n\) 遍 dijkstra 来解决问题,复杂的 \(O(nm\log m)\),可以接受,20pts 到手。
但是它有负权啊,你这做法有个毛线用啊
所以有一个奇怪的想法滋生在我们的脑海中:如果我们将每一个边权都加上一个定值使之为正呢?
这个想法很直接,乍一想好像还挺有道理,正在你暗暗佩服自己的睿智时,我会告诉你:这是错的。
例如对于下图:\(1\) 到 \(2\) 的最短路为 \(1\to 5\to 3\to 2\)。
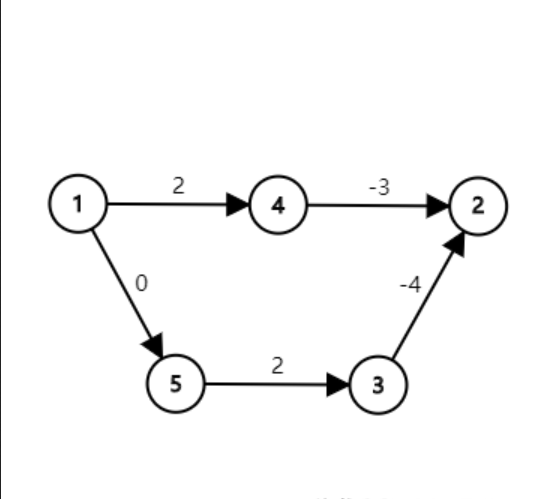
但是在所有边权加上 \(5\) 之后呢?
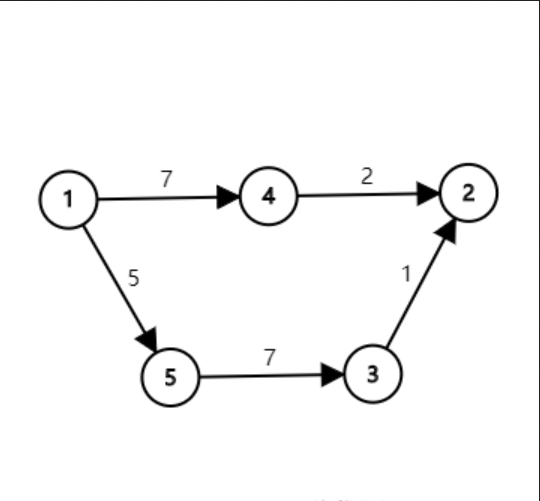
观察上图,发现最短路变成了 \(1\to 4\to 2\),这显然是不对的。
除了有图有真相之外,我们还可以用柯学的方法来解释为什么这是错的:
因为这里的每一条路径增加的并不是一个定值。
例如这里 \(1\to 4\to 2\) 只增加了 \(10\),而 \(1\to 5\to 3\to 2\) 却增加了 \(15\)。
显然在这种情况下,边数少的一条路径更有利,从而导致错误。
那么怎样才能使每一条路径都增加一个定值,每条边权又都变成正数呢?
这就是 Johnson 算法的核心了。
算法概述
Johnson 算法分为两步:
- 预处理势能函数 \(h\)。(人话:跑一遍 spfa)
- 根据势能函数求解全源最短路。(人话:跑 \(n\) 遍 dijkscal)
算法流程
这里先介绍算法流程再介绍正确性,第一遍阅读时能读懂多少就读懂多少,看完下面的证明后再回头看一眼即可。
我们新建一个虚拟节点(在这里我们就设它的编号为 \(0\)),从这个点向其他所有点连一条边权为 \(0\) 的边。
接下来用 Bellman-Ford 算法(spfa 的弱化版)求出从 \(0\) 号点到其他所有点的最短路,记为 \(h_i\)。
假如存在一条从 \(u\) 点到 \(v\) 点,边权为 \(w\) 的边,则我们将该边的边权重新设置为 \(w+h_u-h_v\)。
接下来以每个点为起点,跑 \(n\) 轮 dijkstra 算法即可求出任意两点间的最短路了。
容易看出,该算法的时间复杂度是 \(O(nm\log m)\)。
正确性证明
为什么这样重新标注边权的方式是正确的呢?
提醒一下,本文采用通俗易懂的寓言来描述证明过程,势能什么的还是参考其他人的文章吧。
咳咳,回归正题,为什么这样重新标注边权的方式是正确的呢?
假设重新标记后,\(s\) 到 \(t\) 的路径为 \(s\to p_1\to p_2\to ...\to p_k\to t\)。
那么加权之后的长度表达式为:
\((w(s,p_1)+h_s−h_{p1})+(w(p_1,p_2)+h_{p1}−h_{p2})+⋯+(w(p_k,t)+h_{pk}−h_t)\)
化简后得到:
\(w(s,p_1)+w(p_1,p_2)+ \dots +w(p_k,t)+h_s-h_t\)
那么显然,无论从那个方向走来,\(h_s-h_t\) 始终不变,变化的仅仅是路径上的边权。
即我们引言中的第一个要求:每一条路径都增加一个定值。
接下来我们需要证明新图中所有边的边权非负,因为在非负权图上,dijkstra 算法能够保证得出正确的结果。
根据三角形不等式,新图上任意一边 \((u,v)\) 上两点满足: \(h_v \leq h_u + w(u,v)\)。
这条边重新标记后的边权为 \(w'(u,v)=w(u,v)+h_u-h_v \geq 0\)。这样我们证明了新图上的边权均非负。
至此,我们就证明了 Johnson 算法的正确性。
代码实现
代码实现还是挺简单的,就不做过多介绍了。
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cmath>
#include<queue>
#include<cstdlib>
#define N 30010
#define M 60010
#define INF 1000000000
using namespace std;
int n,m,head[N],cnt=0,sum[N];
long long h[N],dis[N];
bool vis[N];
struct Edge{
int nxt,to,val;
}ed[M];
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
void add(int u,int v,int w){
ed[++cnt].nxt=head[u];
ed[cnt].to=v,ed[cnt].val=w;
head[u]=cnt;
return;
}
void spfa(){
queue<int>q;
memset(h,63,sizeof(h));
memset(vis,false,sizeof(vis));
h[0]=0,vis[0]=true;q.push(0);
while(!q.empty()){
int u=q.front();q.pop();
if(++sum[u]>=n+1){
printf("-1\n");exit(0);
}
vis[u]=false;
for(int i=head[u];i;i=ed[i].nxt){
int v=ed[i].to,w=ed[i].val;
if(h[v]>h[u]+w){
h[v]=h[u]+w;
if(!vis[v]) q.push(v),vis[v]=true;
}
}
}
return;
}
void dijkstra(int s){
priority_queue<pair<long long,int> >q;
for(int i=1;i<=n;i++)
dis[i]=INF;
memset(vis,false,sizeof(vis));
dis[s]=0;
q.push(make_pair(0,s));
while(!q.empty()){
int u=q.top().second;q.pop();
if(vis[u]) continue;
vis[u]=true;
for(int i=head[u];i;i=ed[i].nxt){
int v=ed[i].to,w=ed[i].val;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
if(!vis[v]) q.push(make_pair(-dis[v],v));
}
}
}
return;
}
int main(){
n=read(),m=read();
int u,v,w;
for(int i=1;i<=m;i++)
u=read(),v=read(),w=read(),add(u,v,w);
for(int i=1;i<=n;i++)
add(0,i,0);
spfa();
for(int u=1;u<=n;u++)
for(int j=head[u];j;j=ed[j].nxt)
ed[j].val+=h[u]-h[ed[j].to];
for(int i=1;i<=n;i++){
dijkstra(i);
long long ans=0;
for(int j=1;j<=n;j++){
if(dis[j]==INF) ans+=(long long)j*INF;
else ans+=(long long)j*(dis[j]+h[j]-h[i]);
}
printf("%lld\n",ans);
}
return 0;
}
结语
例题比较难找,之后遇到了会继续 Update 的,同时希望同学们遇到 Johnson 的题目及时私信告诉我。
注意:全文多处引自SF dalao 的文章。
完结撒花

