二叉树
一、树
树形结构是一类重要的非线性结构。树形结构是结点之间有分支,并具有层次关系的结构。它非常类似于自然界中的树。树结构在客观世界中是大量存在的,例如家谱、行政组织机构都可用树形象地表示。树在计算机领域中也有着广泛的应用,例如在编译程序中,用树来表示源程序的语法结构;在数据库系统中,可用树来组织信息;在分析算法的行为时,可用树来描述其执行过程。本章重点讨论二叉树的存储表示及其各种运算,并研究一般树和森林与二叉树的转换关系,最后介绍树的应用实例。
关于树的一些术语
节点的度:一个节点含有的子树的个数称为该节点的度;如上图A结点的度为3,B结点的度为2,c结点的度为1,D结点的度为3。
叶节点或终端节点:度为零的节点称为叶节点;E、F、G、H、I 以及J度都为0
非终端节点或分支节点:度不为零的节点;
双亲节点或父节点:若一个结点含有子节点,则这个节点称为其子节点的父节点;
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
兄弟节点:具有相同父节点的节点互称为兄弟节点;
树的高度或深度:定义一棵树的根结点层次为1,其他节点的层次是其父结点层次加1。一棵树中所有结点的层次的最大值称为这棵树的深度。节点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
树的度:一棵树中,最大的节点的度称为树的度;
树的度是指每个节点孩子的最大数量,上图是3(D点最大是3),而树深度是指树有几层,上图是3
节点的祖先:从根到该节点所经分支上的所有节点;
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
森林:由m(m>=0)棵互不相交的树的集合称为森林;
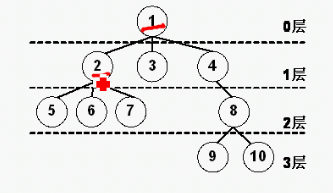
层次遍历为:1,2,3,4,5,6,7,8,9,10
二、二叉树
2.1、二叉树的相关概念
二叉树(BinaryTree)是n(n≥0)个结点的有限集,它或者是空集(n=0),或者由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树的二叉树组成。
完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
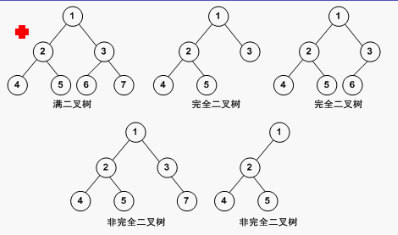
2.2、二叉树的性质:
(1) 在二叉树中,第i层的结点总数不超过2^(i-1)。
(2) 深度为h的二叉树最多有2^h-1个结点(h>=1),最少有h个结点。
(3) 对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1。
(4) 具有n个结点的完全二叉树的深度为int[(log2n)]+1。
(5)有N个结点的完全二叉树各结点如果用顺序方式存储,则结点之间有如下关系:若I为结点编号则 如果I<>1,则其父结点的编号为I/2;如果2*I<=N,则其左儿子(即左子树的根结点)的编号为2*I;若2*I>N,则无左儿子;如果2*I+1<=N,则其右儿子的结点编号为2*I+1;若2*I+1>N,则无右儿子。
(6)给定N个节点,能构成h(N)种不同的二叉树。h(N)为卡特兰数的第N项。h(n)=C(n,2*n)/(n+1)。
(7)设有i个枝点,I为所有枝点的道路长度总和,J为叶的道路长度总和J=I+2i
2.3、二叉树的建立
广义表(Lists,又称列表)是一种非线性的数据结构,是线性表的一种推广。即广义表中放松对表元素的原子限制,容许它们具有其自身结构。它被广泛的应用于人工智能等领域的表处理语言LISP语言中。在LISP语言中,广义表是一种最基本的数据结构,就连LISP 语言的程序也表示为一系列的广义表。(关于广义表的概念,请查看百科的介绍:http://baike.baidu.com/view/203611.htm)
首先,我们采用广义表建立二叉树。我们建立一个字符串类型的广义表作为输入:
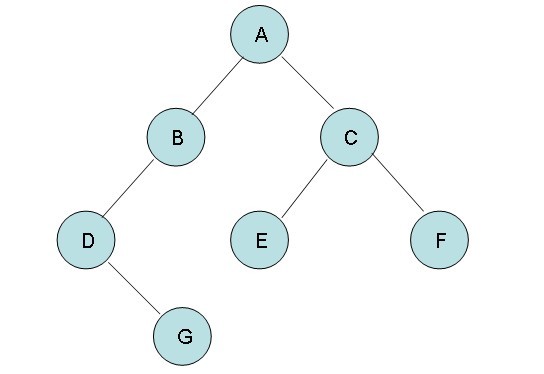
String expression = "A(B(D(,G)),C(E,F))";与该广义表对应的二叉树为:
写代码前,我们通过观察二叉树和广义表,先得出一些结论:
每当遇到字母,将要创建节点
每当遇到“(”,表面要创建左孩子节点
每当遇到“,”,表明要创建又孩子节点
每当遇到“)”,表明要返回上一层节点
广义表中“(”的数量正好是二叉树的层数
根据这些结论,我们基本就可以开始写代码了
二叉树的结点类:
根据广义表创建二叉树的代码如下:
创建完全二叉树:
2.4、二叉树的递归遍历
先序遍历:1 2 4 5 3 6
非递归前序遍历 1 2 4 5 3 6
中序遍历:4 2 5 1 6 3
非递归中序遍历 4,2,5,1,6,3,
后序遍历:4 5 2 6 3 1
非递归后序遍历: 4 5 2 6 3 1
层次遍历:1,2,3,4,5,6,
2.5、树跟二叉树的转换
提醒:二叉树源码下载地址:
http://www.cnblogs.com/tanlon/p/4164309.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号